Demonstate that the inerval energy U of the air in a room is independent of temperature provided the outside pressure p is constant. Calculate U, if p is equal the normal atmosphere pressure and the room's volume is equal to V=40m3.
Intermal energy of air, treating as an ideal as
U=mMCVT=mMRγ−1T=pVγ−1….(1)
Using CV=Rγ−1, since Cp−CV=R an d CpCV=γ
Thus at constant pressure U = constant, because the volume of the room is a constant.
Putting the value of p=patm and V in Eq.(1), we get U=10MJ.
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Kinetic Theory Of Gases
51 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy
47 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
Knowledge Check
Boyle showed that for a given sample of gas at a constant temperature, the product of pressure and volume ,p×V, was always the
Aeven numberBodd numberCwhole numberDsame numberTwo mole of Hydrogen and three mole of Helium are mixed at room temperature and at atmospheric pressure Pa and the mixture occupies a volume V.
ACV of mixture is 2RBCP of mixture is 2.9RCγ of mixture is nearly 1.53DIf the mixture is expanded adiabatically to 2V final pressure is Pa1.42The energy density uV of an ideal gas is related to its pressure P as
AuV=3PBuV=32PCuV=13PDuV=23P
Show that the internal energy of the air (treated as an ideal gas) contained in a room remains constant as the temperature changes between day and gight. Assume that the atmospheric pressure around remains constant and the air in the room maintains this prssure by communicating with the surrounding thourgh the widows, doors, etc.
View SolutionA constant volume air thermometer is used to determine the temperature of a furnace and the excess pressure in the bulb is found to be equal to 152x10−2m of mercury. At 0∘C the pressure in the bulb is equal to that of the atmosphere. If the barometric height throughout the experiment is 76×10−2m of mercury, calculate the temperature of the furnace.
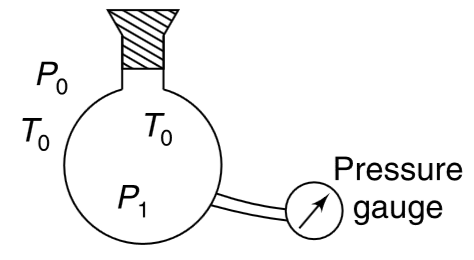
View SolutionAir is filled inside a jar which has a pressure gauge connected to it. The temperature of the air inside the jar is same as outside temperature (=T0) but pressure (P1) is slightly larger than the atmospheric pressure (P0). The stopcock is quickly opened and quickly closed, so that the pressure inside the jar becomes equal to the atmospheric pressure P0. The jar is now allowed to slowly warm up to its original temperature T0. At this time the pressure of the air inside is P2(P0<P2<P1). Assume air to be an ideal gas. Calculate the ratio of specific heats (=γ) for the air, in terms of P0,P1 and P2.
View SolutionFor a given mass of a gas at constant temperature,if the volume,'V' becomes three times then pressure P will become
View SolutionFor a given mass of a gas at constant temperature, if the volume V becomes three times, then the pressure (p) will become :
View Solution
