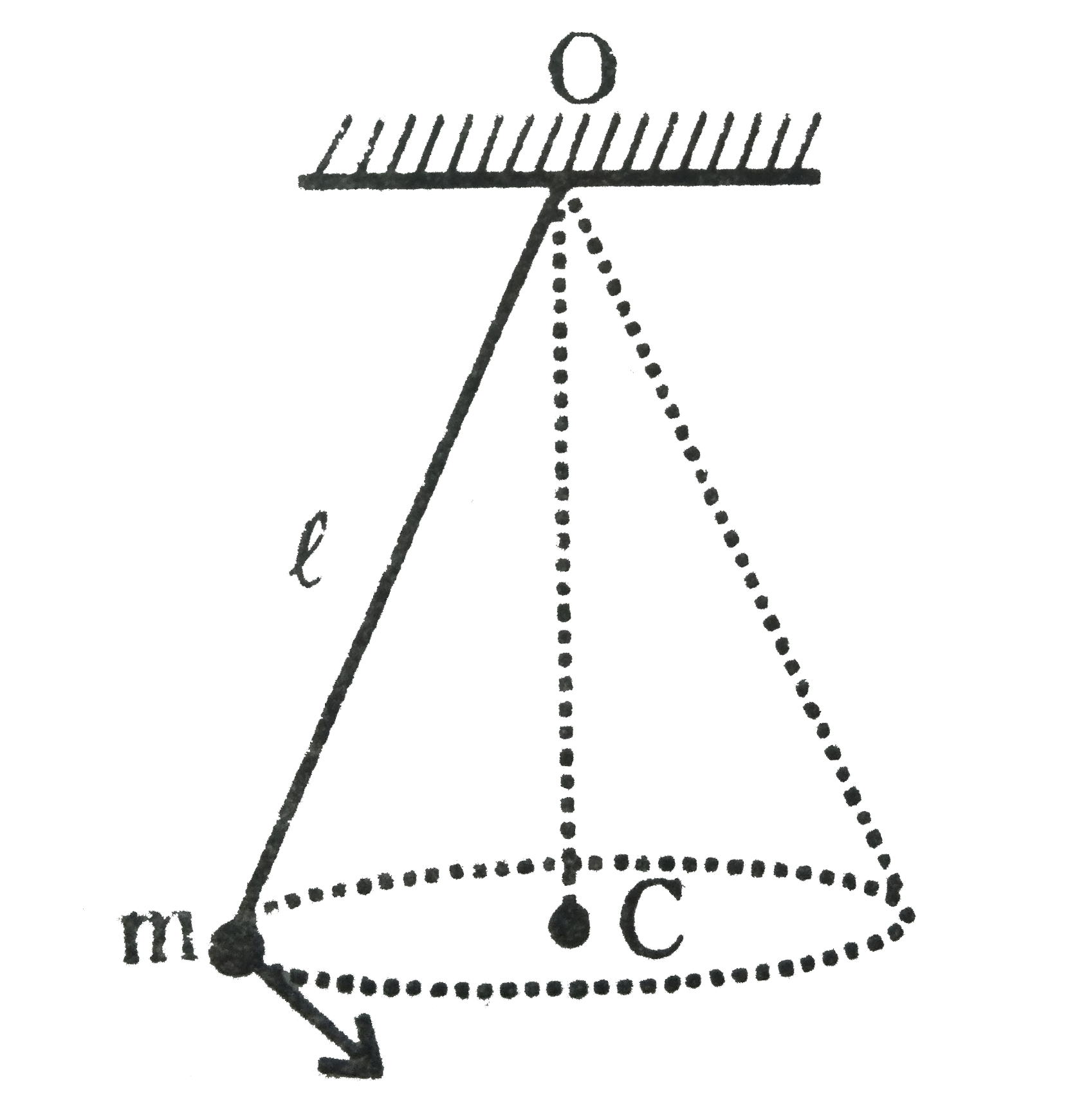
A small ball of mass m suspended from the ceiling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω. Relative to which points does the angular momentum M of the ball remain constant? Find the magnitude of the increment of the vector of the ball's angular momentum relative to the point O picked up during half a revolution.
(a) The ball is under the influence of forces →T and m→g at all the moments of time, while moving along a horizontal circle. Obviously the vertical component of →T balance m→g and so the net moment of these two about any point becomes zero. The horizontal component of →T, which provides the centripetal acceleration to ball is already directed toward the centre (C) of the horizontal circle, thus its moment about the point C equals zero at all the moments of time. Hence the net moment of the force acting on the ball about point C equals zero and that's why the angular mommentum of the ball is conserved about the horizontal circle.
(b) Let α be the angle which the thread forms with the vertical.
Now from equation of particle dynamics:
Tcosα=mg and Tsinα=mω2lsinα
Hence on solving cosα=gω2l (1)
As ∣∣→M∣∣ is constant in magnitude so from figure.
∣∣Δ→M∣∣=2Mcosα where
M=∣∣→Mi∣∣=∣∣→Mf∣∣
=|→rbo×m→v|=mvl (as →rbo⊥→v)
Thus ∣∣Δ→M∣∣=2mvlcosα=2mωl2sinαcosα
=2mglω√1−(gω2t)2 (using 1).

Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Universal Gravitation
Explore 34 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Dynamics Of A Solid Body
Explore 56 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:The Fundamental Equation Of Dynamics
Explore 59 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electromagnetic Waves, Radiation
Explore 36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Transport Phenomena
Explore 38 Videos
Similar Questions
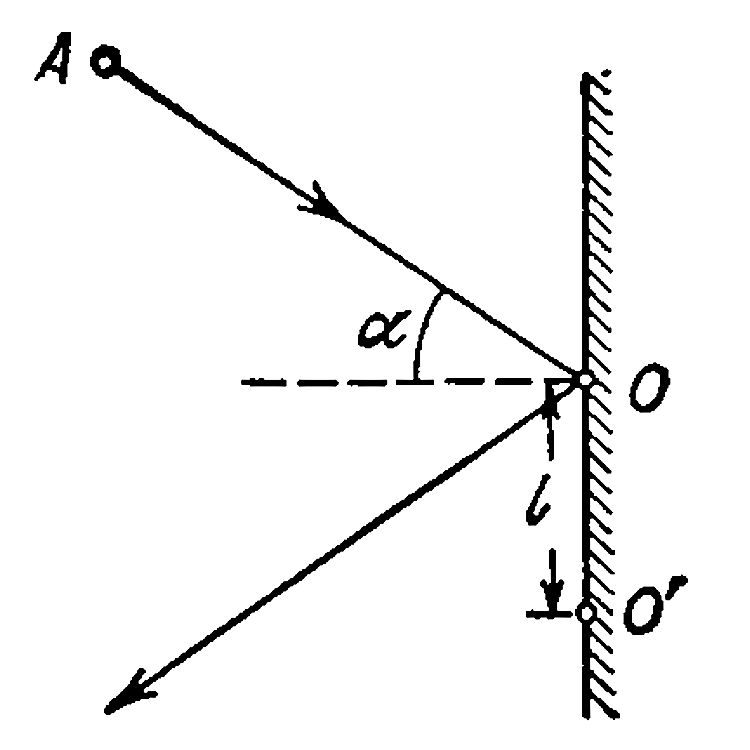
A disc A of mass m sliding over a smooth horizontal surface with velocity v experiences a perfectly elastic collision with a smooth stationary wall at a point O (figure). The angle between the motion direction of the disc and the normal of the wall is equal to α. Find:
(a) the points relative to which the angular momentum M of the disc remains constant in this process,
(b) the magnitude of the increment of the vector of the disc's angular momentum relative to the point O′ which is located in the plane of the disc's motion at the distance l from the point O.
View Solution
A rod of mass 2 kg ad length 2 m is rotating about its one end O wth an angular velocity ω=4rad/s. Find angular momentum of the rod about the axis rotation.
View Solution
Knowledge Check
A small ball of mass m suspended from the celling at a point O by a thread of length l moves along a horizontal circle with a constant angular velocity ω.
 .Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
.Alinear momentum of system (ball + rod) is conservedBangular momentum about C is conservedCkinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collisionDlinear momentum of ball is conserved
A point mass m is suspended from a light thread of length l, fixed at O, is whirled in a horizontal circle at constant speed as shown. From your point of view, stationary with respect to the mass, the forces on the mass areA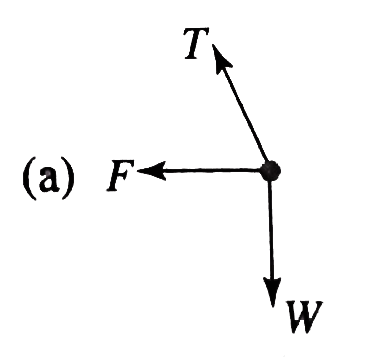 B
B C
C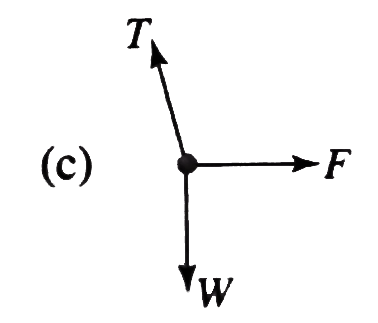 D
D
A rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?
 Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
Amω2l2sinθ6Bmω2l2sin2θ6Cmω2l2sin2θ6Dmω2l2cos2θ6
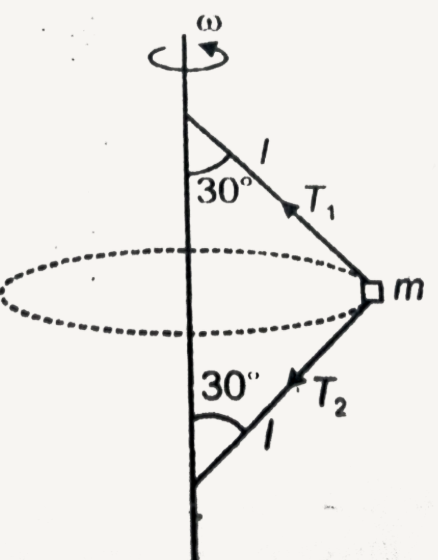
A particle of mass m is whirled in horizontal circle with the help of two threads of length l each as shown in figure . Angular velocity equals ω, then
View SolutionConsider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionRing is fixed on the horizontal surface and a rod starts rotatiing with constant angular velocity ω fixed at O as shown in the figure. Find the magnitude of velocity of intersection points of rod and ring when aplha become 90∘
View Solution

