Two ideal batteries of emfV1andV2 and three resistance R1R2andR3 are connected The current in resistance R2 would be zero if
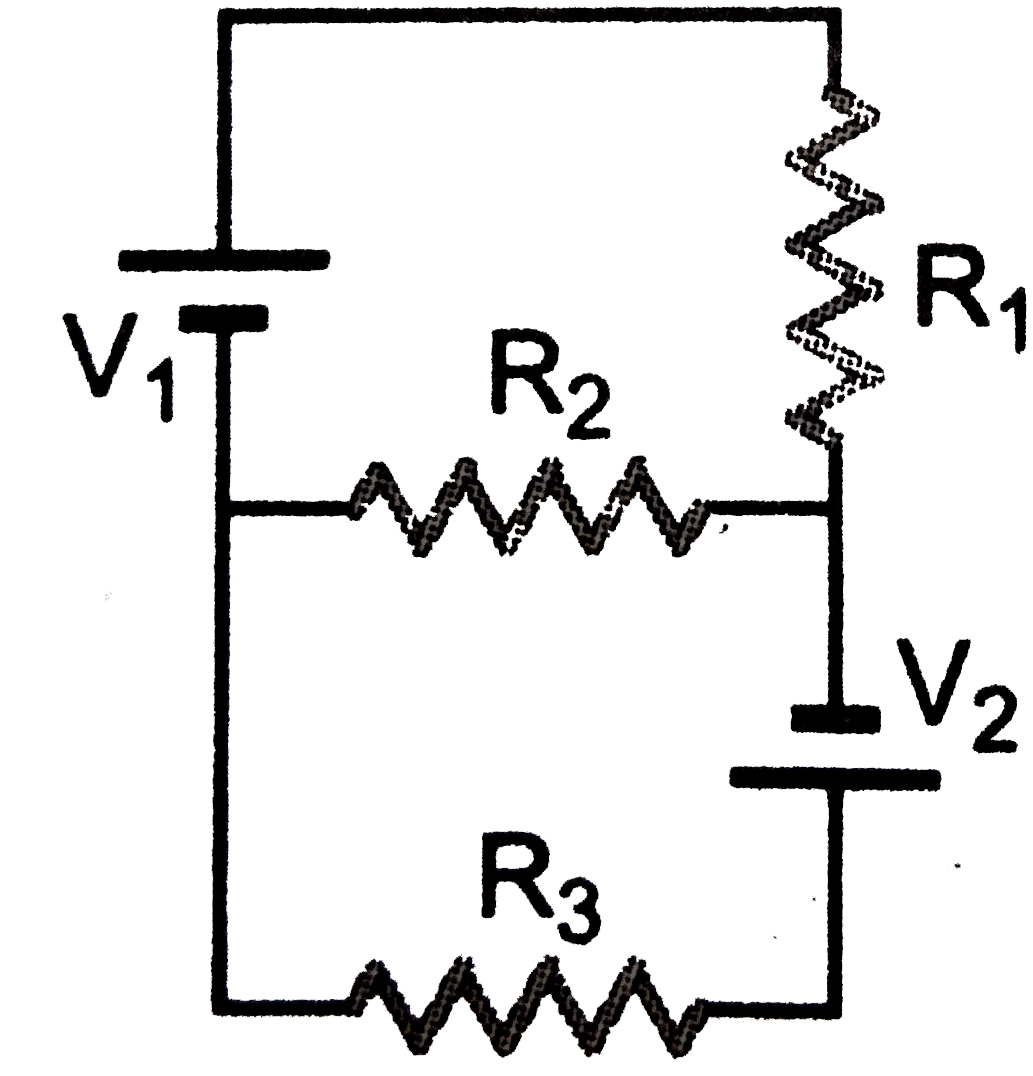
V1=V2andR1=R2=R3
V1=V2andR1=2R2=R3
V1=2V2and2R1=2R2=R3
2V1=V2and2R1=R2=R3
The correct Answer is:a,b,d
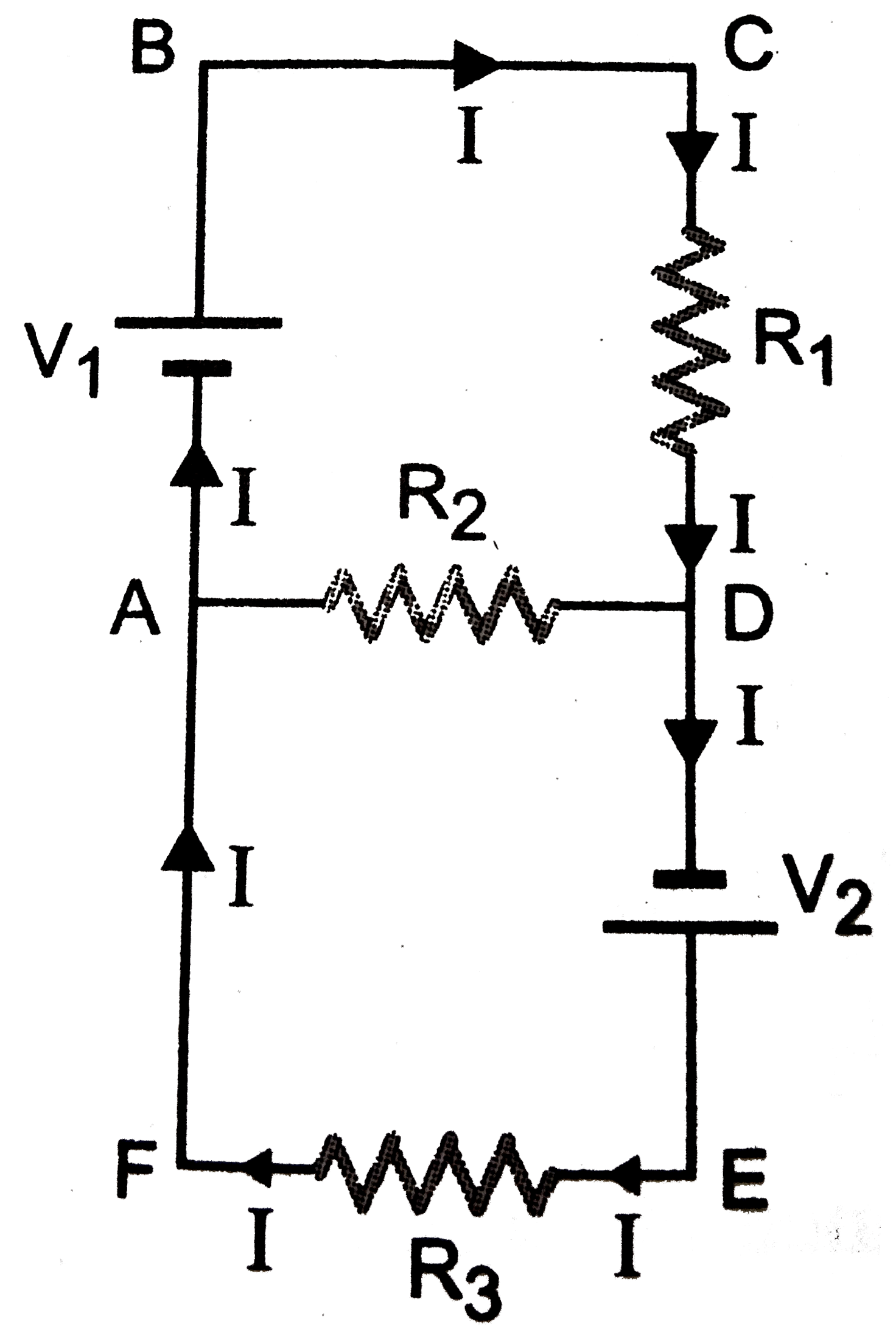
V1=IR1+0×R2orI=V1R1 ….(i)
In closed circuit ABCDEFA we get
V1+V2=IR1+IR2orI=V1+V2R1+R3….(ii)
From (i) and (ii), V1R1=V1+V2R1+R2....(ii)
or V1R1+V1R3=V1R1+V2R1
or V1R3=V2R1.....(iii)
Since current in R2 is zerto R2 can have any value from (ii) we note that if V1=V2 Then
R1=R3=R2orR1=2R1+R3
If V1=2V2,R1=2R3
If 2V1=V2,R3=3R1=R2
Thus option (a,b and d) are true .
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Jee (main and advance)
Explore 4 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Interger Type
Explore 2 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Value based
Explore 2 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
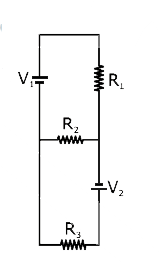
Two ideal batteries of emf V1andV2 and these resistances R1,R2andR3 are connected as shown in the figure . The current in resistance R2 would be zero if
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View Solution
Knowledge Check
Two ideal batteries of emf V1andV2 and three resistances R1,R2andR3 are connected as shown in the figure. The current in resistance R2 would be zero if
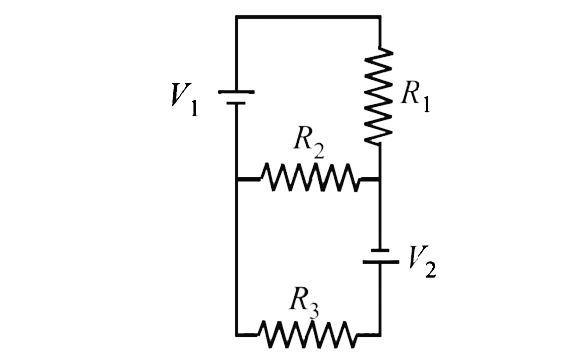 AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and3R1=R2=R3
AV1=V2andR1=R2=R3BV1=V2andR1=2R2=R3CV1=2V2and2R1=2R2=R3D2V1=V2and3R1=R2=R3Three batteries of emf E1,E2 and E3 and internal resistance r1,r2 and r3 are connected as shown. The current through the battery of emf E3 is zero if.
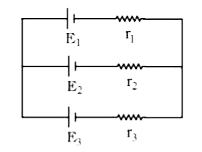 AE1r2+E2r1=E3(r1+r2)BE1r2−E2r1=E3(r1+r2)CE1r2+E2r1=E3(r1+r2)DE1r1+E2r2=E3(r1+r2)
AE1r2+E2r1=E3(r1+r2)BE1r2−E2r1=E3(r1+r2)CE1r2+E2r1=E3(r1+r2)DE1r1+E2r2=E3(r1+r2)Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
AThe effective emf of this parallel combination is (ε1r1+ε2r2)(r1+r2)BThe effective internal resistance of this combination is 2r1r2(r1+r2)Cthe effective emf of this parallel combination is (ε1r2+ε2r1)(r1+r2)DThe effective internal resistance of this combination is r1r2(r1+r2)
If resistors of resistance R1 and R2 are connected in parallel,then resultant resistance is "
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure

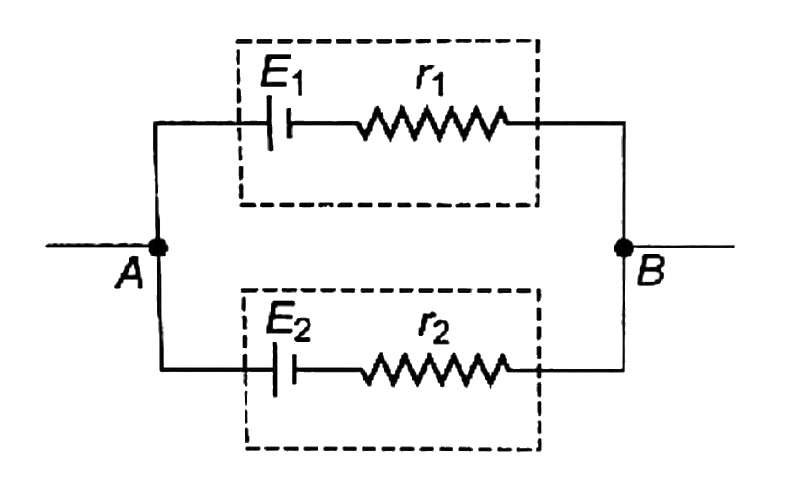
View SolutionTwo batteries of emf E1 and E2(E2>E1) and internal resistance r1 and r2 respectively are connected in parallel as shown in the figure. Then, which of the followings statements is correct ?
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View Solution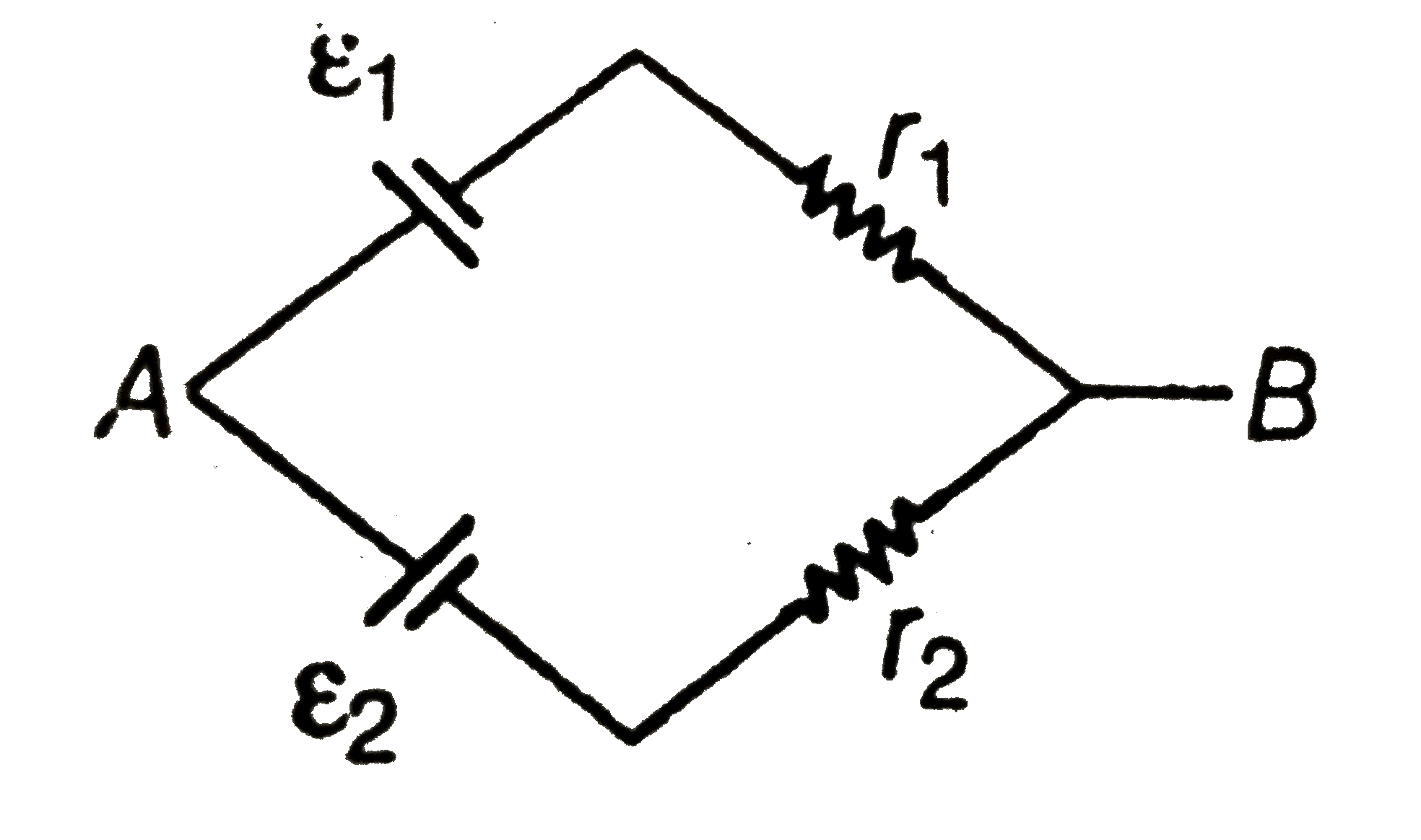
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.
View Solution