Eleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
Let ABCDFGHK be the open cube formed by joining eleven equal wires each of resistance 2Ω
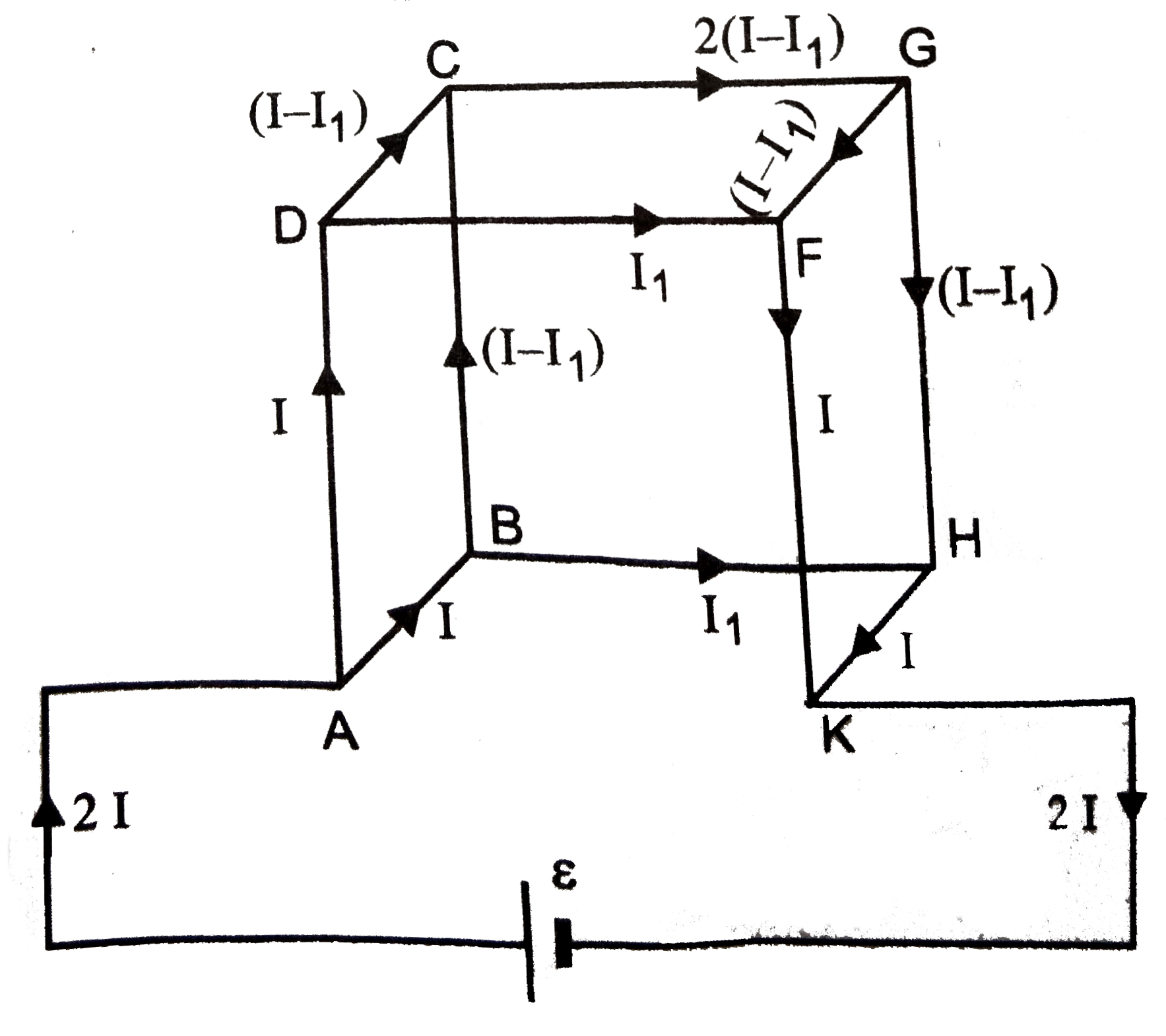
Let the current from the cell of emf ε enter the cube at corner A and after passing through all the wires leave at K, the other end of the open edge of the cube.
For the sake of convenience, let us suppose that the total current is 2I. At A, this current is divided into two parts : I along AB and I AD. This is beacuse the resistances of the two paths are equal. At the points B and D, each part of current is further divided into two uneqaul parts. The distribution of current in the various arms of skeleton cube is shown according to Kirchhoff's first rule. The current leaving the cube at K is again 2 I. Let R be the equivalent resistance of skeleton cube between edges A and K.
From Ohm's law, ε=2IR
Applying Kirchhoff's second rule to mesh ε ABHKε , we have
ε=2×I+2×I1+2×I
or ε=4I+2I1
Applying Kirchhoff's Second rule to mesh of DFGCD, we have
2I1−2(I−I1)−2×2(I−I1)−2(I−I1)=0
2I1−2I+2I1−4I+4I1+2I+2I1=0
or 101−8I=0or8I=10I1
or I1=810I=45I
From (ii) and (iii),
ε=4I+2(45I)=28I5
From (i) and (iv),
2Ir=28I5orR=285×2=2.8Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Conceptual Problems
Explore 3 Videos
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Very short Q/A
Explore 7 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:MODEL TEST PAPER-2
Explore 9 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
Similar Questions
Eleven equal wires each of resistance r form the edges of a incomplete cube. Find the total resistance from one end of the vacant edge of the cube to the other.
View SolutionTwelve identical wires each of resistance 6Ω are joined to from a skeleton cube. Find the resistance between the current of the same edge of the cube
View Solution
Knowledge Check
Twelve equal wires each of resistance rΩ form a cube. The effective resistance between the corners of the same edge of the cube is
A712rB127rC57rD125rFind the total surface area of a cube of edge 5 m.
A125 m2B250 m2C150 m2D300 m2Find the total surface area of a cube of edge 5 m.
A125m2B250m2C6m3D11m3
The edge of a cube is 3 cm. Find the total surface area and the volume of the cube.
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
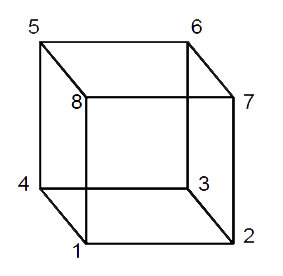
When current enters at 1 and leaves at 2
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
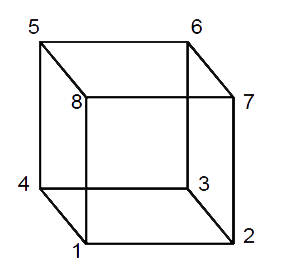
When current enters at 1 and leaves at 3
View SolutionTwelve equal resistors each R Ω are connected to from the edges of a cube . Find the equivalent resistance of the network.
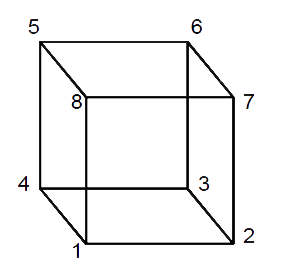
When current enters at 1 & leaves at 6 (body diagonal)
View SolutionEach edge of a cube is increased by 50%. Find the percentage increase in the surface area of the cube.
View Solution

