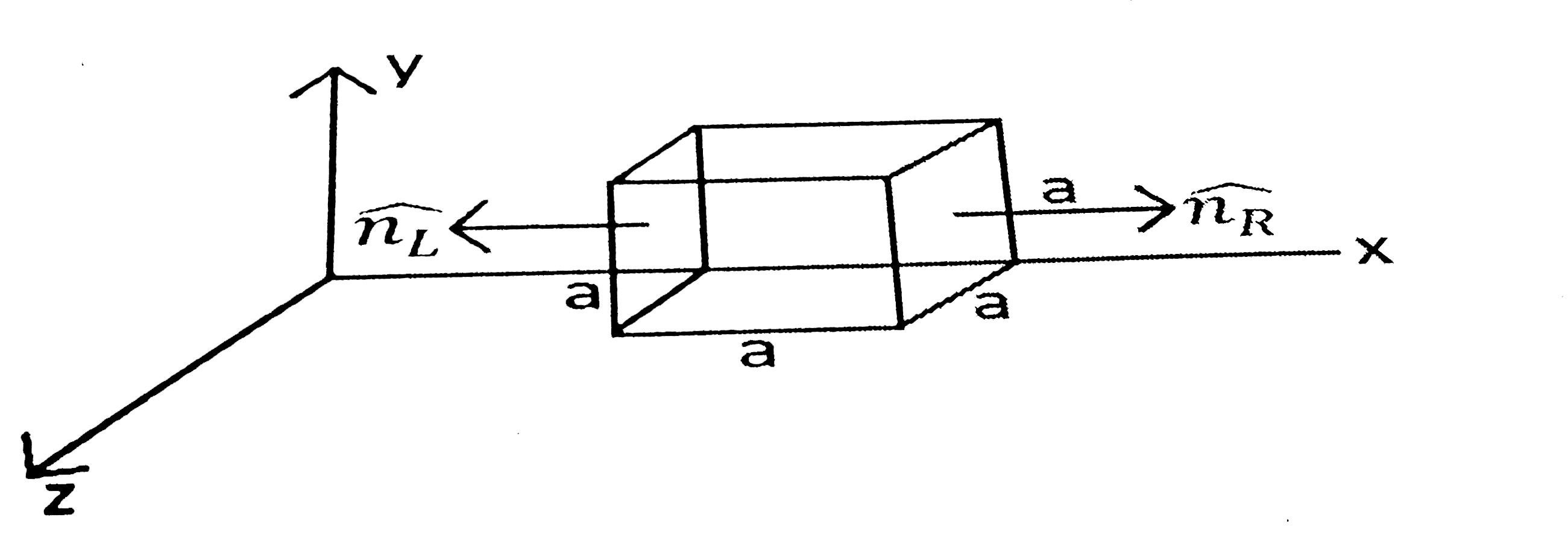
In Fig, electric field is dirceted along +X direction and is given by Ex=5Ax+2B, where E is in NC−1 and x is in meter, A and B are constants having dimenstions. Taking A=10NC−1m−1andB=5NC−1, calculate (i) the electric flux through the cube and (ii) net charge enclosed within the cube.
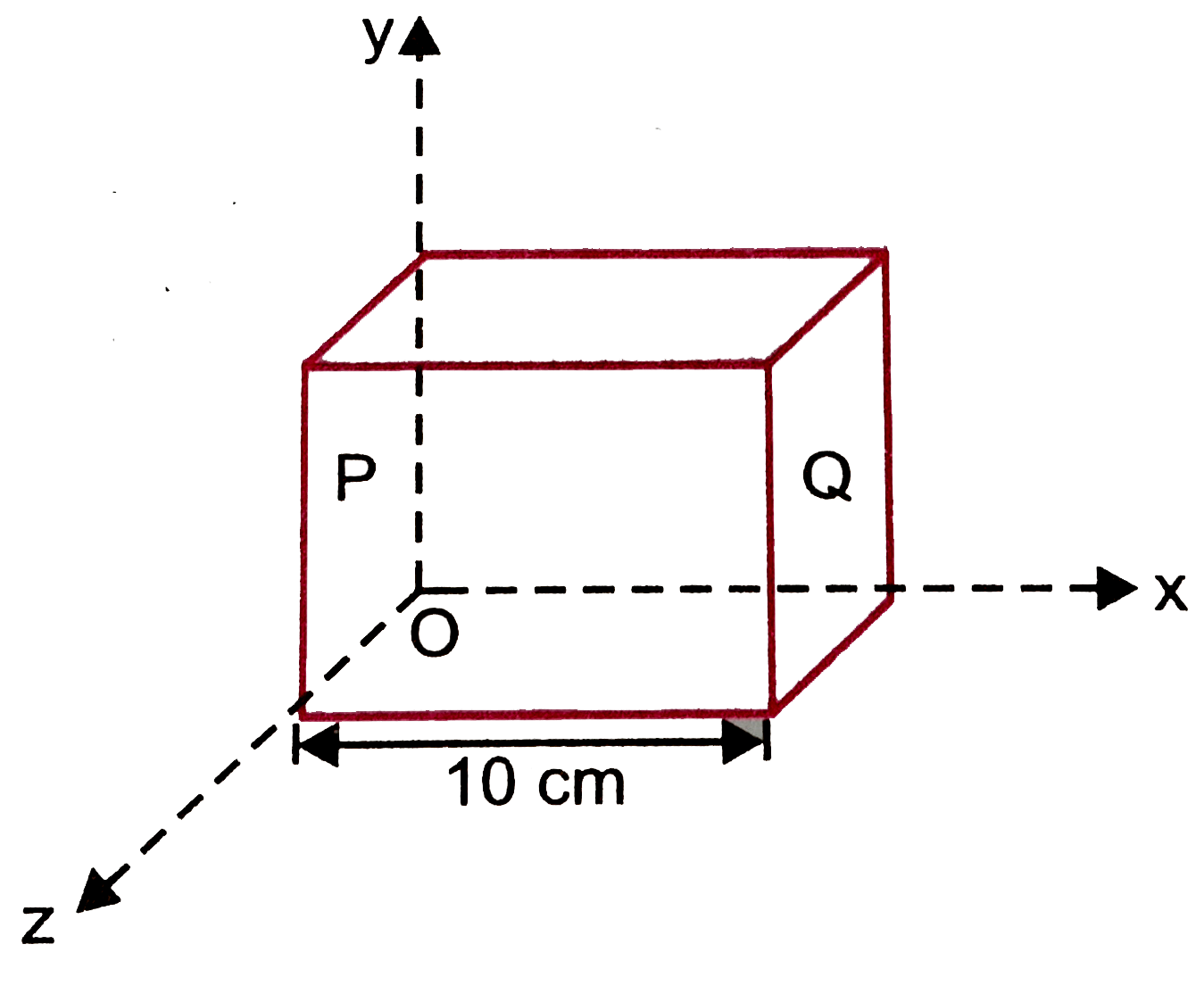
Here, A=10NC−1m−1,B=NC−1
Ex=5Ax+2B
As electric field is directed along =q direction along +x direction, therefore electric flux is asscociated with faces P and Q only.
Area of each face, ds=10×10cm2=10−2m2.
For face P:x=0
From (i) Ex=2B=2×5=10NC−1,
Electric flux through face P,ϕ1=Exdscos180∘=10×10−2×(−1)=0.1NC1m2
For face Q : x=10cm=10−1m
From (i) Ex=5×10(10−1)+2×5=15NC−1
∴ Electric flux through face Q=ϕ2=Exdscosθ∘=15×10−2+15×10−2=5×10−2=5×10−2NC−1m2
From Gauss's therorem, ϕ=q∈0
q=∈0ϕ=8.85×10−12×5×10−2=0.4425×10−12C

Similar Questions
Knowledge Check
In the given electric field →E=[α(d+x)ˆi+E0ˆj]NC−1, where α=1NC−1 hypothetical closed surface is taken as shown in figure .
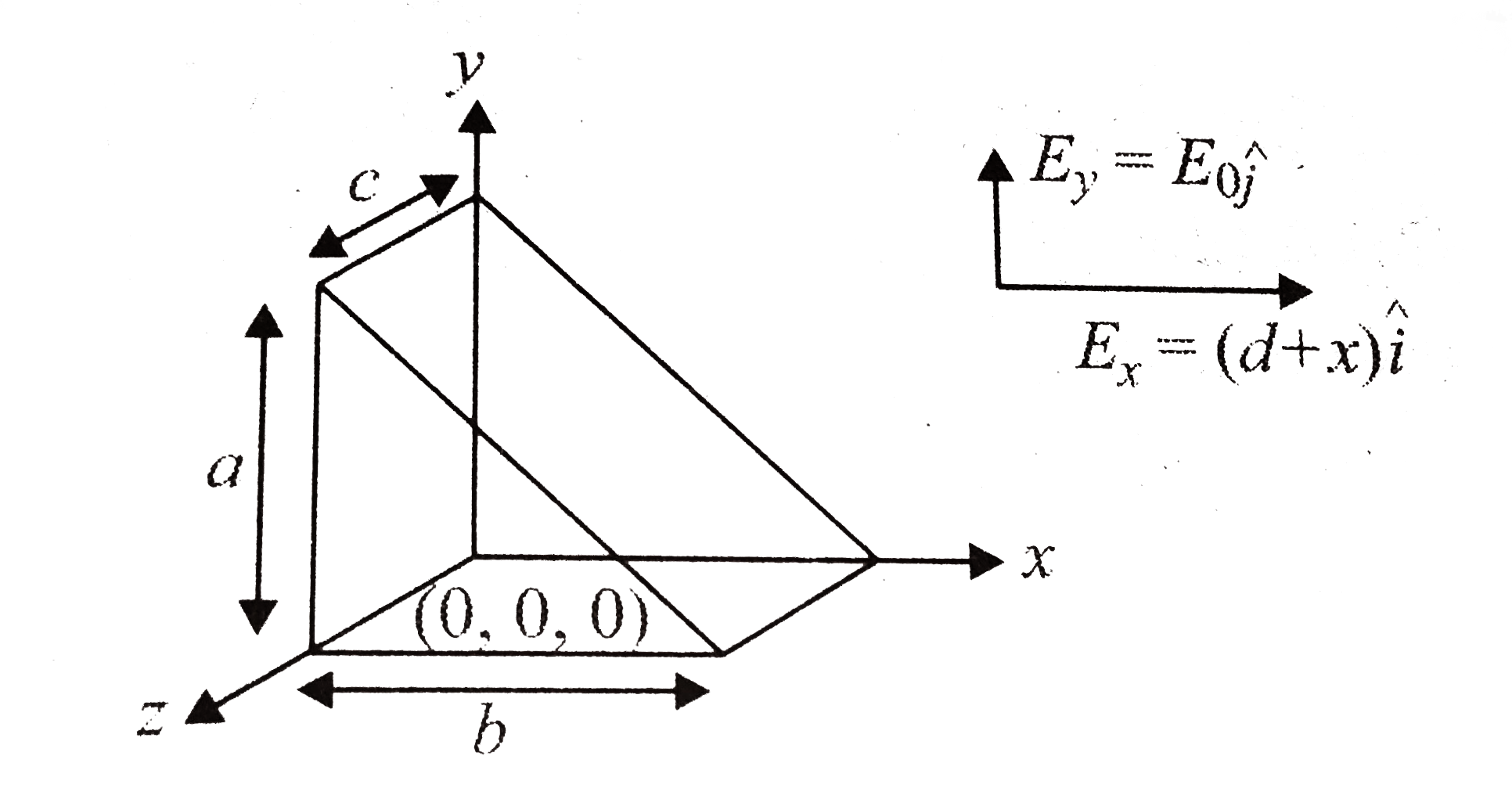
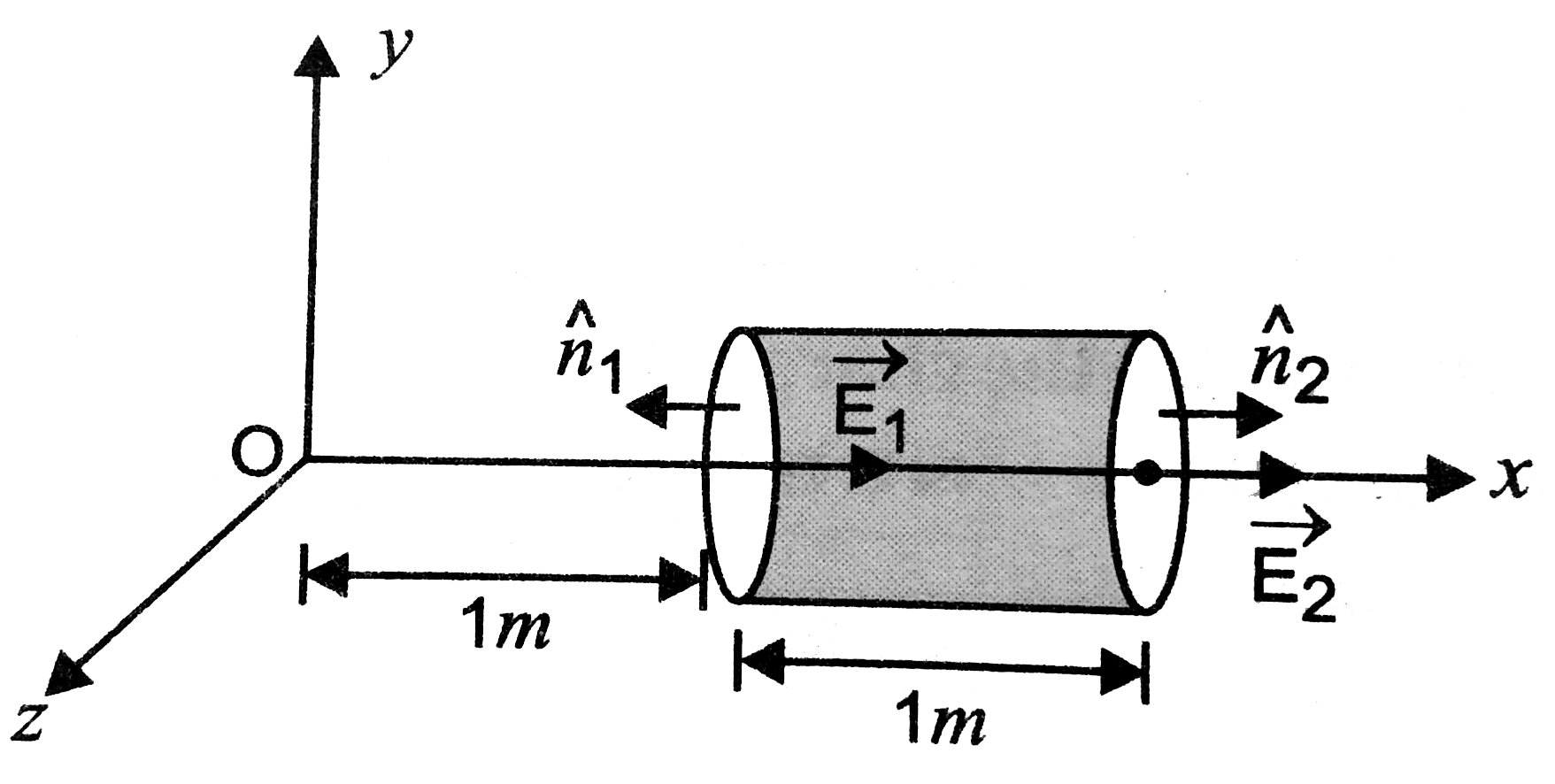
The total charge enclosed within the close surface isAabcε02Bacdε02Cabdε02Dnone of theseA hollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
 A(i) 0.625Nm2/C , (ii) 3.506×10−12CB(i) 0.125Nm2/C , (ii) 1.106×10−12CC(i) 0.330Nm2/C , (ii) 2.550×10−12CD(i) 2.125Nm2/C , (ii) 6.106×10−12C
A(i) 0.625Nm2/C , (ii) 3.506×10−12CB(i) 0.125Nm2/C , (ii) 1.106×10−12CC(i) 0.330Nm2/C , (ii) 2.550×10−12CD(i) 2.125Nm2/C , (ii) 6.106×10−12C
The electric field componets due to a charge inside the cube of side 0.1m are Ex=αx, where α=500(N/C)m−1,
Ey=0,Ez=0. Calculate the flux through the cube and the charge inside the cube.
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
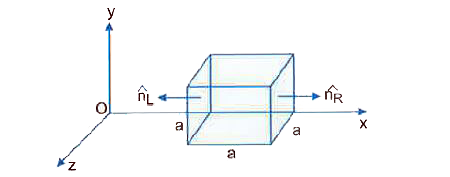
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View SolutionDefine electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1m area as shown in Ex=αx, where α=500N/Cm,EY=0andEZ=0.
Calculate (i) the flux through the cube , and
(ii) the charges inside the cube.

View SolutionThe electric field in an electromagnetic wave is given by: E=(50NC−1)sinω(t−xc)F∈dthe∫ensity(∈W/m^2 ) of the wave.
View SolutionElectric field at origin due to a point charge 1nC placed at (1,1)m in x−yplane is
View Solution