A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The total flux passing through the cube is
−0.135Nm2C−1
−0.054Nm2C−1
0.081Nm2C−1
zero
The correct Answer is:B
For S1,→A=L2(−ˆj),→E=−5xˆi+3zˆk.
Here →E⊥→A , so ϕs1=0.
For S2,→A=L2ˆk,→E=−5xˆi+3Lˆk.
Here −5xˆi is perpendicular to →A , so no flux due to this component.
ϕs2=(3Lˆk).L2ˆk=3L3=81×10−3Nm2C−1
For S3,→A=L2ˆj,→E=−5xˆi+3zˆk.
Here →E⊥→A , so ϕs3=0.
For S4,→A=−L2ˆk,→E=−5xˆi+0ˆk (since z=0).
Here →⊥→A , so ϕS4=0.
For S5,→A=L2ˆi,→E=−5Lˆi+3zˆk.
No flux due to 3zˆk component.
ϕS5=(−5Lˆi).L2ˆi=−5L3=−135×10−3Nm2C−1
ForS6,→A=−L2ˆi,→E=0ˆi+3zˆk ( since x=0).
Here →E⊥→A , so ϕs6=0.
Total flux through the cube is ϕ=ϕ(S1+S2+S3+S5+S6)
=81×10−3−135×10−3=−54×10−3Nm2C−1
Now , ϕ=q∈ε0orq∈=ϕε0=−0.054ε0C
Topper's Solved these Questions
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Subjective type
Explore 7 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:MCQ s
Explore 38 Videos
- ELECTRIC FLUX AND GAUSS LAWBook:CENGAGE PHYSICSChapter:ELECTRIC FLUX AND GAUSS LAWExercise:Multiple Correct
Explore 8 Videos
- ELECTRIC CURRENT AND CIRCUITBook:CENGAGE PHYSICSChapter:ELECTRIC CURRENT AND CIRCUITExercise:Interger
Explore 8 Videos
- ELECTRIC POTENTIALBook:CENGAGE PHYSICSChapter:ELECTRIC POTENTIALExercise:DPP 3.5
Explore 14 Videos
Similar Questions
A cube has sides of length L=0.2m. It is placed with one corner at the origin as shown in figure. The electric field is uniform and given by E=(2.5N/C)ˆi−(4.2N/C)ˆj. Find the electric flux through the entire cube.
View SolutionA cube has sides of length L=0.2 m It is placed with one corner at the origin as shown in figure The electric field in uniform and given by →E=(2.5ˆi−4.2ˆj)N/C .Find the electric flux through the entire cube.

View Solution
Knowledge Check
A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The flux passing through the surface S5 will beA−0.135Nm2C−1B−0.054Nm2C−1C0.081Nm2C−1D0.054Nm2C−1A cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The total electric charge inside the cube isA−0.054ε0CB0.081ε0CC0.135ε0CD0.054ε0CA cube has sides of length L=0.300m. It is placed with one corner at the origin ( refer to Fig.2.119).The electric field is not uniform but is given by →E=(−5.00NC−1)xˆi+(3.00NC−1)zˆk.
The surface that have zero flux areAS2,S4,andS5BS1,S3,S4,andS6CS1,S2,andS3DS2,S3,andS4
The cube in figure has edge length √2m and is oriented as shown in a region of uniform electric field , in newtons per coulomb, is given by (a)6.00ˆi,(b)−2.00ˆj,and(c)−3.00ˆj+4.00ˆk . (d) what is the total flux through the cube for each field ?
View SolutionA cube has sides of length L. It is placed with one corner at the origin ( refer to Fig.2.119). The electric field is uniform and given by →€=−Bˆi+Cˆj−Dˆk , where B,C,andD are positive constants.
The total flux passing through the cube is
View SolutionA cube has sides of length L. It is placed with one corner atAthe origin as shown in figure. The electric field is uniform and given by E=−Bˆi+Cˆj−Dˆk, where B, C and D are positive constants.
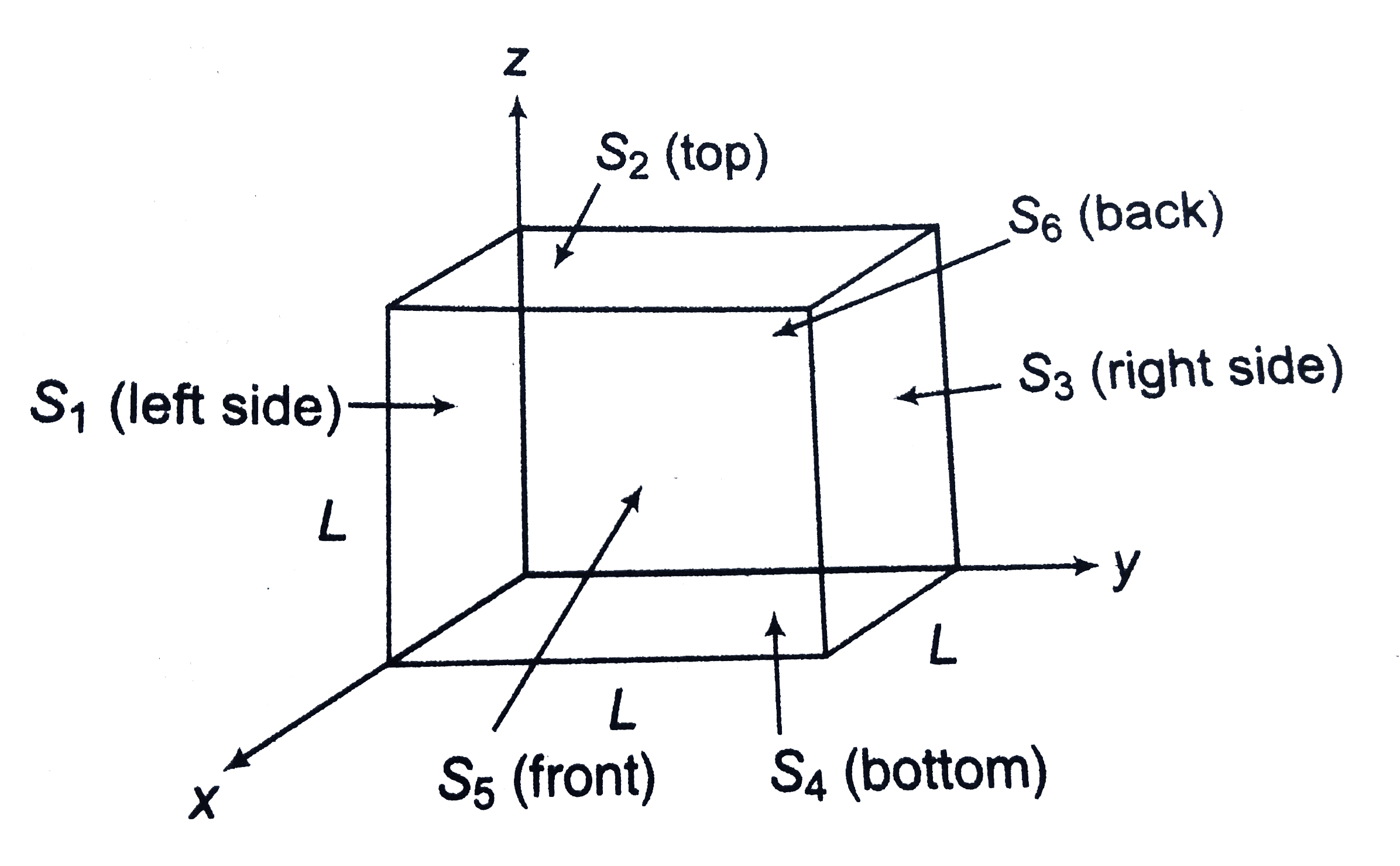
(a) Find the electric flux through each of the six cube faces S1,S2,S3,S4andS5andS6.
(b) Find the electric flux through the entire cube.
View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0ˆk. Total electric flux passing through the cube would be
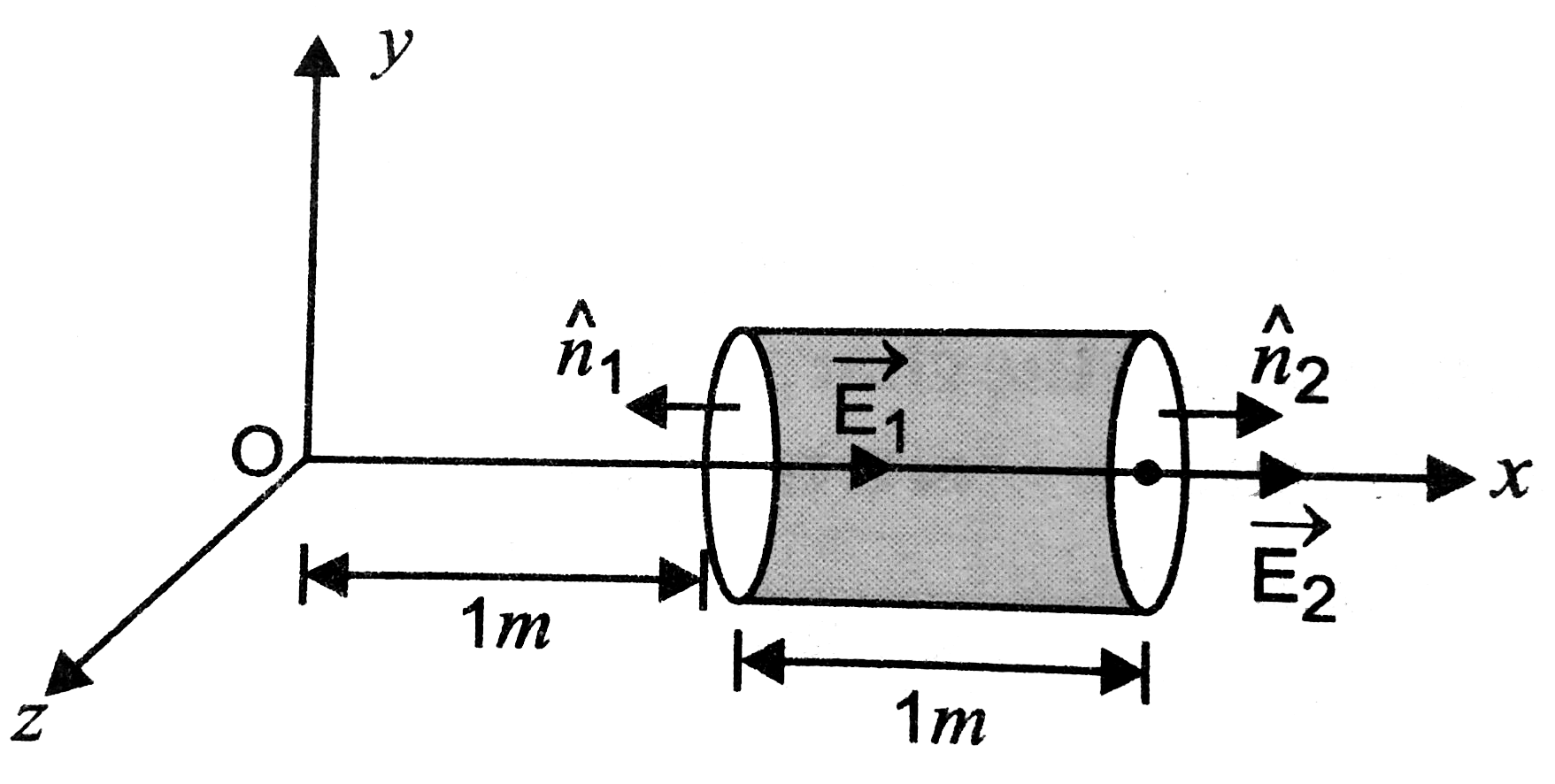
View SolutionA hollow cylindrical box of length 1m and area of cross section 25cm2 is placed in a three dimensional co-ordinate system as shown in Fig, The electric field in the
region is given by →E=50xˆi , where E is in NC−1 and x is in meter. Find
(i) Net flux through the cylinder
(ii) Charge enclosed by the cylinder.
View Solution

