Consider the previous problem , let the outer shell have the charge $- 4 q$ . As in the above problem , the inner shell has the charge $+ 2 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for

zero

$\frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$

$- \frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$

$\frac{1}{4 π ε_{0}} \frac{6 q}{r^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

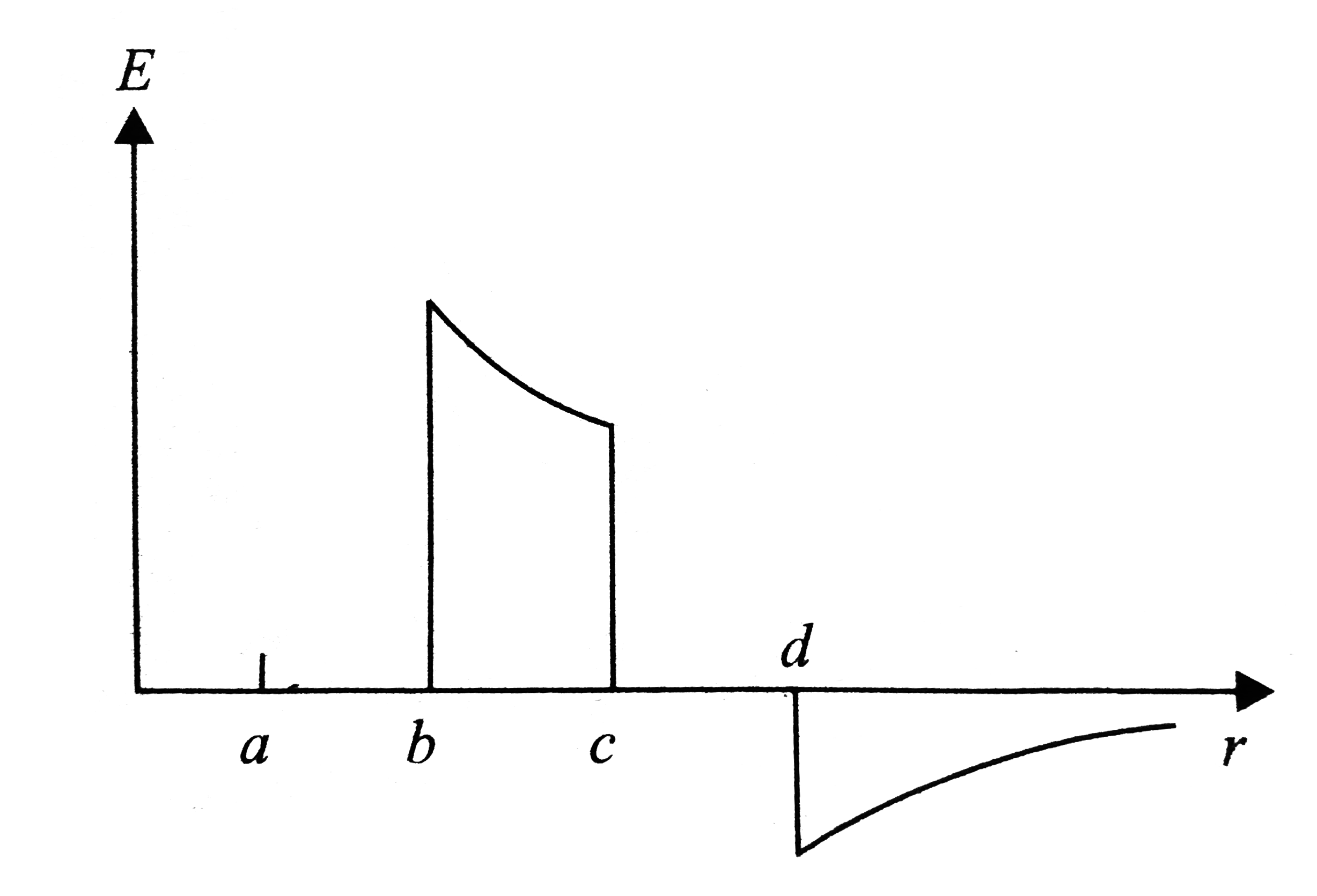
i. $r < a . E = 0$ , since charge enclosed is zero.
ii. $a < r < b . E = 0$ , since charge enclosed is zero.
iii. $b < r < c . E = \frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$ , since charge enclosed is $+ 2 q$ .
iv. $c < r < d . E = 0$ , since charge enclosed is zero ( Fig. S2.55).
v. $r > d . E = - \frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$ , since charge enclosed is $- 2 q$ .

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Knowledge Check

A small conducting spherical shell with inner radius $a$ and outer radius $b$ is concentric with a larger conducting spherical shell with inner radius $c$ and outer radius $d$ ( as shown in Fig . 2.121). The inner shell has a total charge $+ 2 q$ , and the outer shell has a total charge $+ 4 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for

$b < r < c$
Azero
B $\frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$
C $- \frac{1}{4 π ε_{0}} \frac{6 q}{r^{2}}$
D $\frac{1}{4 π ε_{0}} \frac{q}{r^{2}}$
A small conducting spherical shell with inner radius $a$ and outer radius $b$ is concentric with a larger conducting spherical shell with inner radius $c$ and outer radius $d$ ( as shown in Fig . 2.121). The inner shell has a total charge $+ 2 q$ , and the outer shell has a total charge $+ 4 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for

$a < r < b$
Azero
B $\frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$
C $- \frac{1}{4 π ε_{0}} \frac{6 q}{r^{2}}$
D(1)/( 4 pi epsilon_(0)) (q)/( r^(2))
A small conducting spherical shell with inner radius $a$ and outer radius $b$ is concentric with a larger conducting spherical shell with inner radius $c$ and outer radius $d$ ( as shown in Fig . 2.121). The inner shell has a total charge $+ 2 q$ , and the outer shell has a total charge $+ 4 q$ . Calculate the electric field in terms of $q$ and the distance $r$ from the common center of the two shells for

$c < r < d$
Azero
B $\frac{1}{4 π ε_{0}} \frac{2 q}{r^{2}}$
C $- \frac{1}{4 π ε_{0}} \frac{6 q}{r^{2}}$
D $\frac{1}{4 π ε_{0}} \frac{q}{r^{2}}$