The electric field componets due to a charge inside the cube of side 0.1m are Ex=αx, where α=500(N/C)m−1,
Ey=0,Ez=0. Calculate the flux through the cube and the charge inside the cube.
To solve the given problem, we need to calculate the electric flux through the cube and the charge inside the cube. Let's break down the solution step by step.
Step 1: Calculate the Electric Flux through the Left Face of the Cube
The electric field component in the x-direction is given by Ex=αx, where α=500N/C⋅m−1.
1. Determine the area vector for the left face:
- The left face of the cube is at x=0.
- The area vector →A for the left face points in the negative x-direction.
2. Calculate the flux through the left face:
- The electric field at x=0 is Ex=α⋅0=0.
- The area of the face A=(0.1m)2=0.01m2.
- The angle between →E and →A is 180∘.
Φ1=Ex⋅A⋅cos(180∘)=0⋅0.01⋅(−1)=0N⋅m2/C
Step 2: Calculate the Electric Flux through the Right Face of the Cube
1. Determine the area vector for the right face:
- The right face of the cube is at x=0.1m.
- The area vector →A for the right face points in the positive x-direction.
2. Calculate the flux through the right face:
- The electric field at x=0.1m is Ex=α⋅0.1=500⋅0.1=50N/C.
- The area of the face A=(0.1m)2=0.01m2.
- The angle between →E and →A is 0∘.
Φ2=Ex⋅A⋅cos(0∘)=50⋅0.01⋅1=0.5N⋅m2/C
Step 3: Calculate the Net Electric Flux through the Cube
The net flux through the cube is the sum of the fluxes through all its faces. Since the electric field only has a component in the x-direction, the flux through the other faces (y and z faces) is zero.
Φnet=Φ1+Φ2=0+0.5=0.5N⋅m2/C
Step 4: Calculate the Charge Inside the Cube
Using Gauss's law, the net flux through a closed surface is related to the charge enclosed by:
Φnet=qinsideϵ0
Where ϵ0=8.85×10−12C2/(N⋅m2).
qinside=Φnet⋅ϵ0=0.5⋅8.85×10−12=4.425×10−12C
Final Answer
- Electric Flux through the Cube: 0.5N⋅m2/C
- Charge Inside the Cube: 4.425×10−12C
The electric field component in the x-direction is given by Ex=αx, where α=500N/C⋅m−1.
- The left face of the cube is at x=0.
- The area vector →A for the left face points in the negative x-direction.
- The electric field at x=0 is Ex=α⋅0=0.
- The area of the face A=(0.1m)2=0.01m2.
- The angle between →E and →A is 180∘.
1. Determine the area vector for the right face:
- The right face of the cube is at x=0.1m.
- The area vector →A for the right face points in the positive x-direction.
- The electric field at x=0.1m is Ex=α⋅0.1=500⋅0.1=50N/C.
- The area of the face A=(0.1m)2=0.01m2.
- The angle between →E and →A is 0∘.
The net flux through the cube is the sum of the fluxes through all its faces. Since the electric field only has a component in the x-direction, the flux through the other faces (y and z faces) is zero.
Using Gauss's law, the net flux through a closed surface is related to the charge enclosed by:
- Electric Flux through the Cube: 0.5N⋅m2/C
- Charge Inside the Cube: 4.425×10−12C
Similar Questions
(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
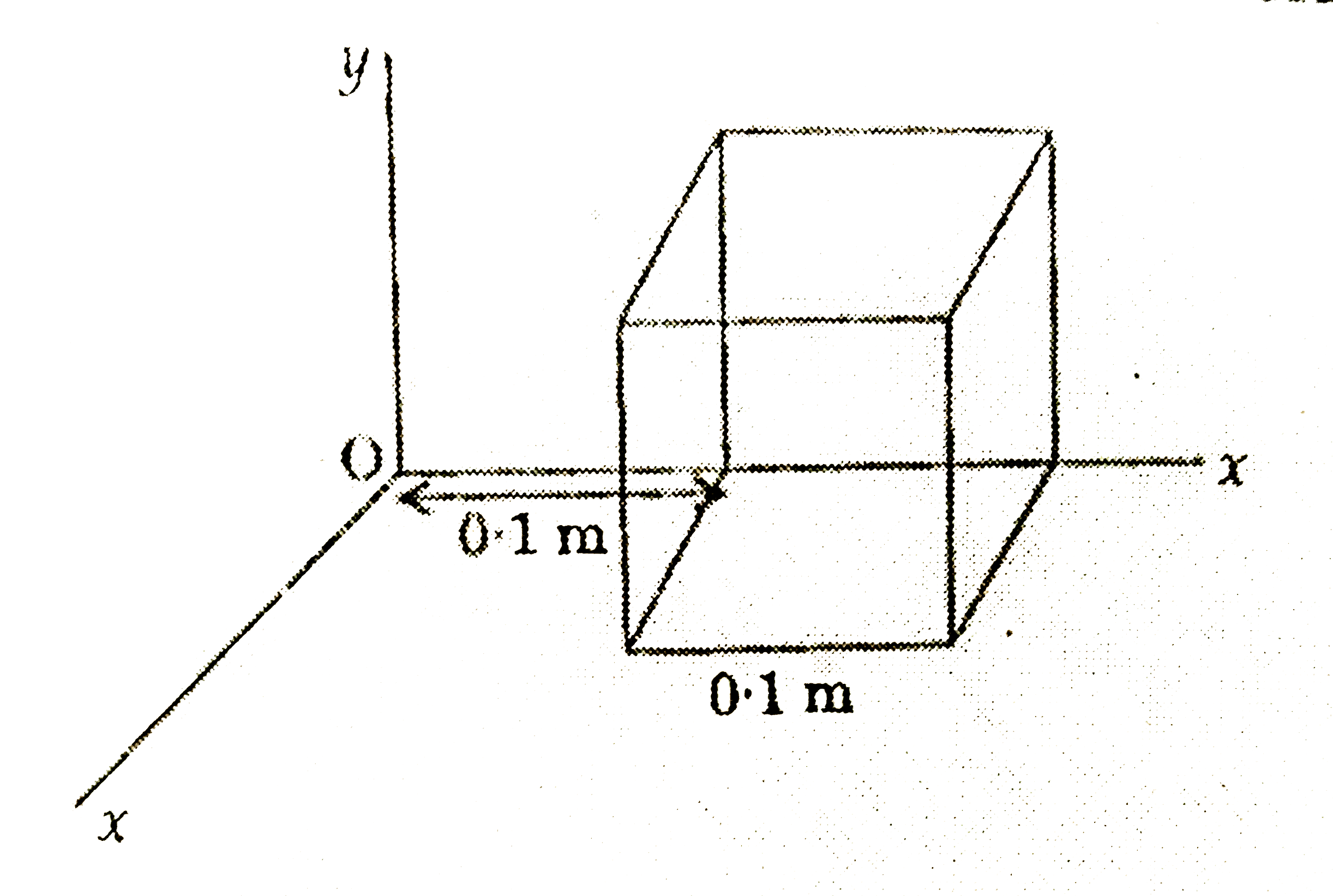
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.
View SolutionDefine electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1m area as shown in Ex=αx, where α=500N/Cm,EY=0andEZ=0.
Calculate (i) the flux through the cube , and
(ii) the charges inside the cube.

View Solution
Knowledge Check
Electric flux through a cube with charge q inside is
Aqε0Bq6ε0Cq3ε0D0Due to a charge inside the cube, the electric field is: Ex = 600x, Ey = 0, Ez = 0. The charge inside the cube is nearly -
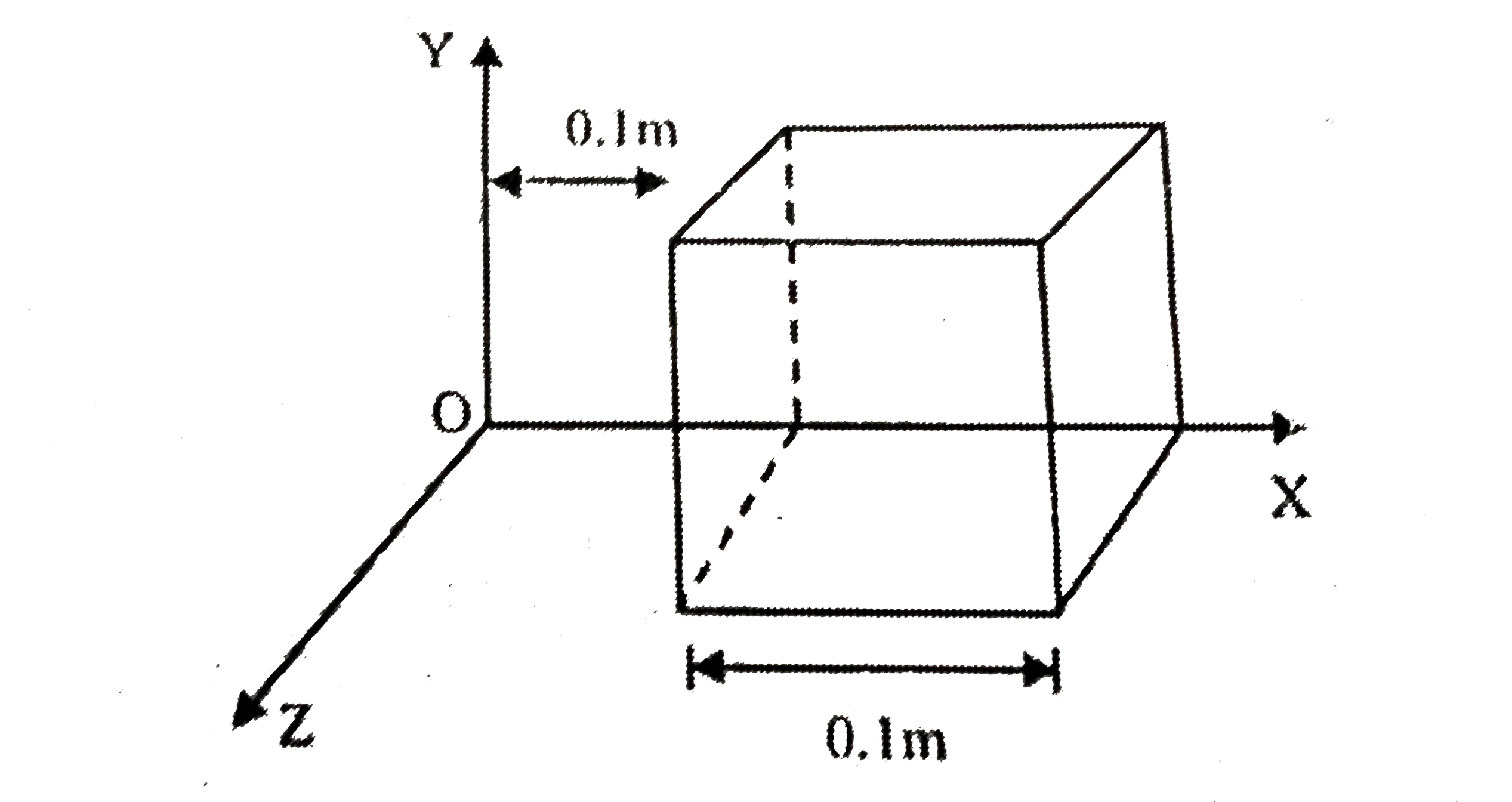 A600μCB60μCC53μCD6μC
A600μCB60μCC53μCD6μCA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0ˆk. Total electric flux passing through the cube would be
AE0a2B2E0a2C6E0a2DNone of these
Using Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
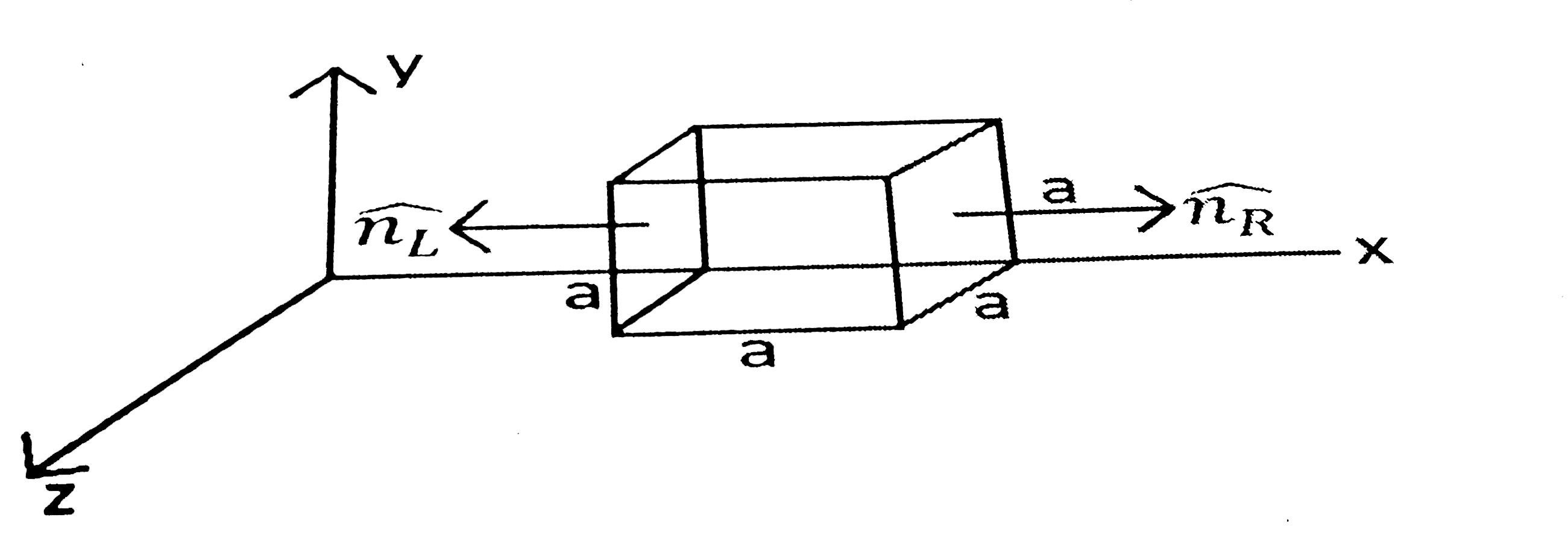
View Solution(a) Using Gauss's law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
(b) The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/Cm. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a=0.1m.
View SolutionDefine electric flux and write its SI unit . The electric field components in the figure shown are : Ex=αx,Ey=0,Ez=0 where α=100NCm.
Calculate the charge within the cube , assuming a = 0.1 m .
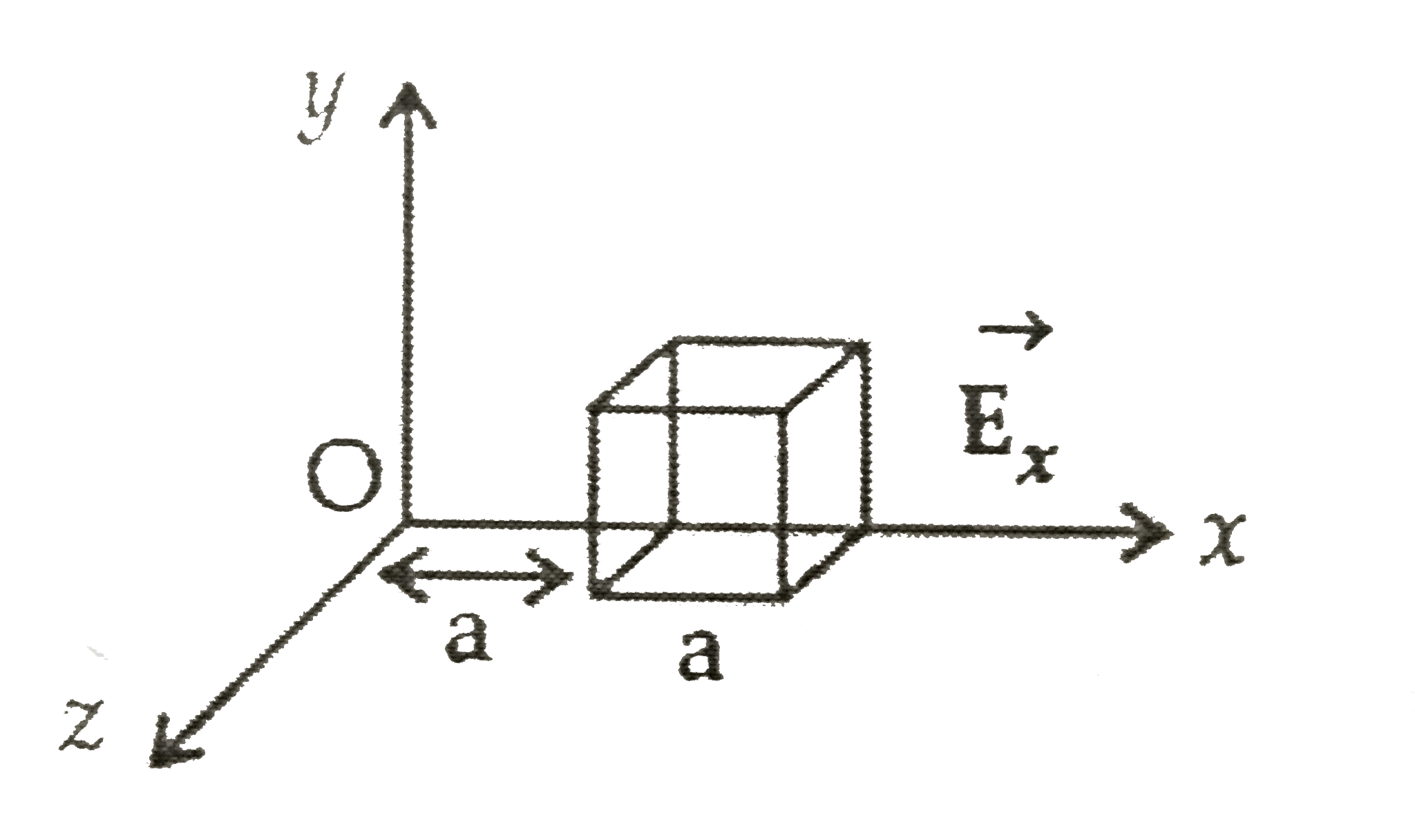
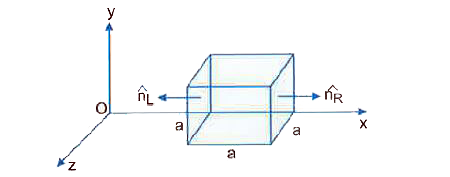
View SolutionGiven the components of an electric field as Ex=αx,Ey=0 and Ez=0, where α is a dimensional constant. Calculate the flux through each face of the cube of side a, as shown in the figure.

View SolutionThe electric components in the figure are Ex=αx1/2,Ey=0,Ez=0 where α=800N/m2 if a=0.1m is the side of cube then the charge with in the cube is
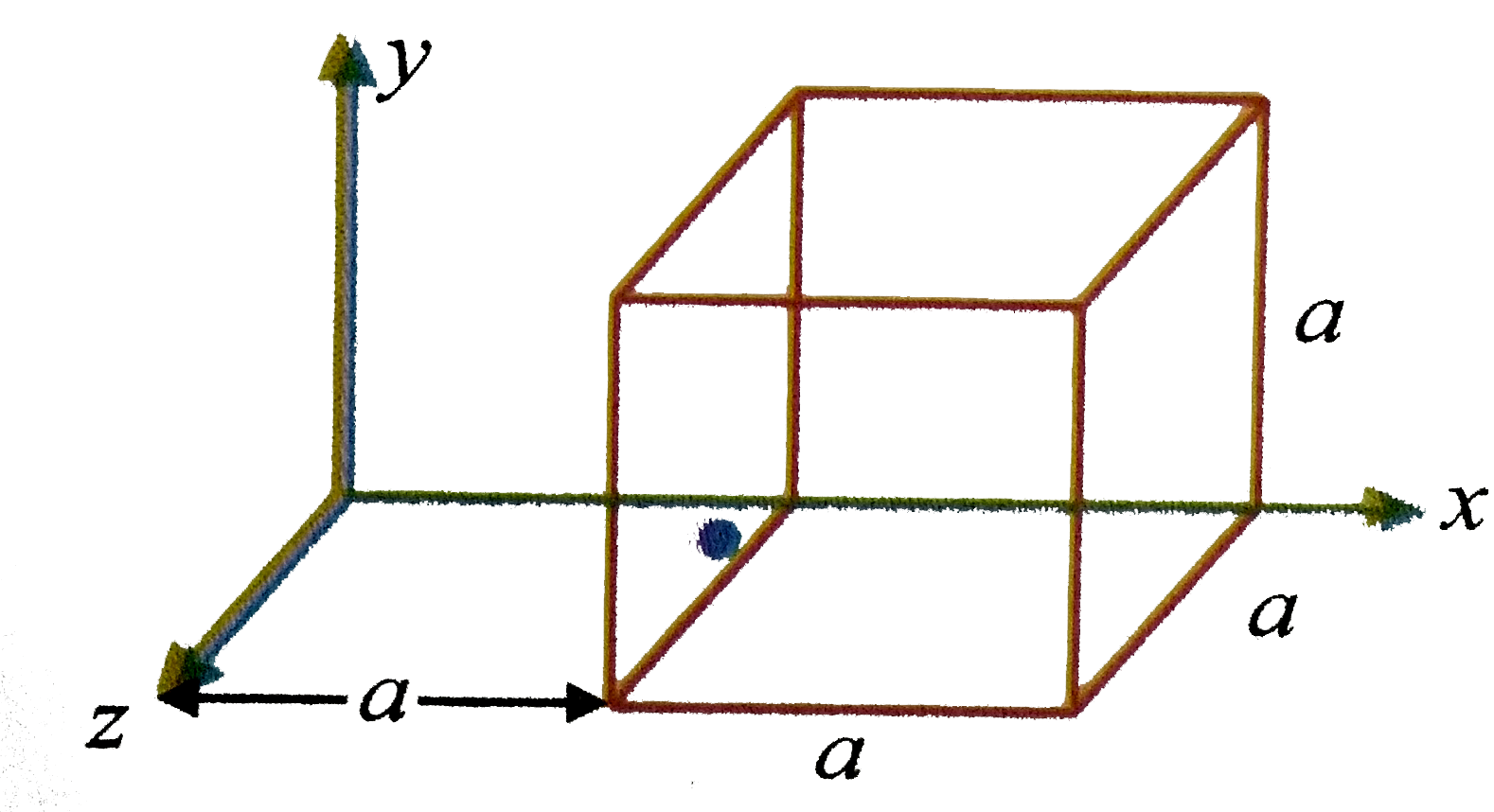
View Solution

