A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P (0,0,3 cm) to a point Q (0,4 cm, 0) via a point R (0,6 cm, 9cm).
To solve the problem of calculating the work done in moving a charge from point P to point Q via point R, we can follow these steps:
Step 1: Understand the Given Information
- Charge at the origin, Q=8mC=8×10−3C
- Charge to be moved, q0=−2×10−9C
- Point P coordinates: (0,0,3cm)=(0,0,0.03m)
- Point Q coordinates: (0,4cm,0)=(0,0.04m,0)
Step 2: Calculate the Potential at Point P
The electric potential V due to a point charge is given by the formula:
V=14πϵ0Qr
Where:
- ϵ0=8.85×10−12C2/N m2 (permittivity of free space)
- r is the distance from the charge to the point where the potential is being calculated.
For point P:
- Distance rP=3cm=0.03m
Calculating the potential at point P:
VP=14π(8.85×10−12)8×10−30.03
VP=9×109×8×10−30.03=2.4×108V
Step 3: Calculate the Potential at Point Q
For point Q:
- Distance rQ=4cm=0.04m
Calculating the potential at point Q:
VQ=14π(8.85×10−12)8×10−30.04
VQ=9×109×8×10−30.04=1.8×108V
Step 4: Calculate the Potential Difference
The potential difference ΔV between points Q and P is:
ΔV=VQ−VP=1.8×108−2.4×108=−6×107V
Step 5: Calculate the Work Done
The work done W in moving the charge q0 through the potential difference ΔV is given by:
W=q0ΔV
Substituting the values:
W=(−2×10−9)×(−6×107)=1.2J
Final Answer
The work done in taking the charge from point P to point Q is 1.2J.
---
- Charge at the origin, Q=8mC=8×10−3C
- Charge to be moved, q0=−2×10−9C
- Point P coordinates: (0,0,3cm)=(0,0,0.03m)
- Point Q coordinates: (0,4cm,0)=(0,0.04m,0)
The electric potential V due to a point charge is given by the formula:
V=14πϵ0Qr
Where:
- ϵ0=8.85×10−12C2/N m2 (permittivity of free space)
- r is the distance from the charge to the point where the potential is being calculated.
- Distance rP=3cm=0.03m
VP=14π(8.85×10−12)8×10−30.03
VP=9×109×8×10−30.03=2.4×108V
For point Q:
- Distance rQ=4cm=0.04m
VQ=14π(8.85×10−12)8×10−30.04
VQ=9×109×8×10−30.04=1.8×108V
The potential difference ΔV between points Q and P is:
ΔV=VQ−VP=1.8×108−2.4×108=−6×107V
The work done W in moving the charge q0 through the potential difference ΔV is given by:
W=q0ΔV
Substituting the values:
W=(−2×10−9)×(−6×107)=1.2J
The work done in taking the charge from point P to point Q is 1.2J.
Similar Questions
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P(0,0,3 cm) to a point Q10,4 cm, 0) via a point R(0,6 cm, 9 cm).
View SolutionA charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9 from a point P(0,0,3cm) to a point Q (0,4cm,0) via a point R(0,6cm,9cm).
View Solution
Knowledge Check
Calculate the work done in taking a charge −2×10−9C from A to B via C (in diagram )
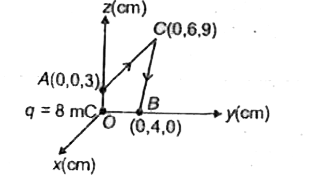 A0.2 jouleB1.2 jouleC2.2 jouleDzero
A0.2 jouleB1.2 jouleC2.2 jouleDzeroAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
 A(−qQ4πε01a2)√2aBzeroC(qQ4πε01a2)1√2D(qQ4πε01a2)1√2a
A(−qQ4πε01a2)√2aBzeroC(qQ4πε01a2)1√2D(qQ4πε01a2)1√2aAs per this diagram a point charge +q is placed at the origin O. Work done in taking another point charge −Q from the point A(0,a) to another point B(a,0) along the staight path AB is:
 AzeroB(−qQ/4πε0)(1/a2)√2aC(qQ/4πε0)(1/a2).a/√2D(qQ/4πε0)(1/a2)√2a
AzeroB(−qQ/4πε0)(1/a2)√2aC(qQ/4πε0)(1/a2).a/√2D(qQ/4πε0)(1/a2)√2a
The work done in moving a charge of 2×10−9 C from a point of potential - 3000 V to another point P is 5×10−5J . Find the potential at the point P.
View Solution(a) Calculate the potential at a point P due to a charge of 4×10−7C located 9 cm away.
(b) Hence obtain the work done in bringing a charge of 2×10−9C from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
View SolutionTwo charges −qand+q are located at points A(0,0,−a)andB(0,0+a). How much work is done in moving a test charge from point (b,0,0) to Q(−b,0,0) ?
View SolutionA charge of 0.5 nC is placed at the centre of an equilateral triangle of side 10 cm, calculate the work done in bringing a charge of 0.1 nC from infinity to any vertices of the triangle.
View SolutionCalculate the work done by electric field in moving an electron from point A(0, 2 cm) to point B(5cm, 9cm) in a region of electric field →E=104ˆjVm−1
View Solution

