The work done in moving a charge of 2×10−9 C from a point of potential - 3000 V to another point P is 5×10−5J . Find the potential at the point P.
To find the potential at point P, we can use the relationship between work done, charge, and potential difference. The work done (W) in moving a charge (Q) through a potential difference (ΔV) is given by the formula:
W=Q⋅ΔV
Where:
- W is the work done (in joules),
- Q is the charge (in coulombs),
- ΔV is the change in electric potential (in volts).
Step 1: Identify the known values
We know:
- Charge, Q=2×10−9C
- Initial potential, VA=−3000V
- Work done, W=5×10−5J
Step 2: Write the equation for work done
The work done in moving the charge from point A to point P can be expressed as:
W=Q⋅(VP−VA)
Step 3: Substitute the known values into the equation
Substituting the known values into the equation gives:
5×10−5=2×10−9⋅(VP−(−3000))
Step 4: Simplify the equation
This simplifies to:
5×10−5=2×10−9⋅(VP+3000)
Step 5: Solve for VP+3000
To isolate VP+3000, divide both sides by 2×10−9:
VP+3000=5×10−52×10−9
Calculating the right side:
VP+3000=52×104=2.5×104
Step 6: Solve for VP
Now, subtract 3000 from both sides:
VP=2.5×104−3000
Step 7: Calculate VP
Calculating the above expression gives:
VP=25000−3000=22000V
Final Answer
Thus, the potential at point P is:
VP=22000V
---
- W is the work done (in joules),
- Q is the charge (in coulombs),
- ΔV is the change in electric potential (in volts).
We know:
- Charge, Q=2×10−9C
- Initial potential, VA=−3000V
- Work done, W=5×10−5J
The work done in moving the charge from point A to point P can be expressed as:
Substituting the known values into the equation gives:
This simplifies to:
To isolate VP+3000, divide both sides by 2×10−9:
Now, subtract 3000 from both sides:
Calculating the above expression gives:
Thus, the potential at point P is:
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENIALBook:NN GHOSHChapter:ELECTRIC FIELD AND POTENIALExercise:EXERCISE
Explore 21 Videos
- ELECTRIC FIELD AND POTENIALBook:NN GHOSHChapter:ELECTRIC FIELD AND POTENIALExercise:EXERCISE-B
Explore 35 Videos
- DYNAMO, MOTOR, TRANSFORMERBook:NN GHOSHChapter:DYNAMO, MOTOR, TRANSFORMERExercise:EXERCISE
Explore 8 Videos
- ELECTROMAGNETIC INDUCTIONBook:NN GHOSHChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERICISES-B
Explore 18 Videos
Similar Questions
Knowledge Check
On moving a charge of 2C from a point A where potential is +12V to a point B where potential is -12 V, the work done is -
A+24JB−24JC48 JD−48JHow much work is done in moving a charge of 4 C across two points havng a P.D. of 10 V ?
A40 JB0.4 JC2.5 JD4 JHow much work is done in moving a charge of 4 C across two points having a potential difference if 12 V ?
A48 JB3 JC40 JD12 J
A charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P(0,0,3 cm) to a point Q10,4 cm, 0) via a point R(0,6 cm, 9 cm).
View SolutionA charge of 8 mC is located at the origin. Calculate the work done in taking a small charge of −2×10−9C from a point P (0,0,3 cm) to a point Q (0,4 cm, 0) via a point R (0,6 cm, 9cm).
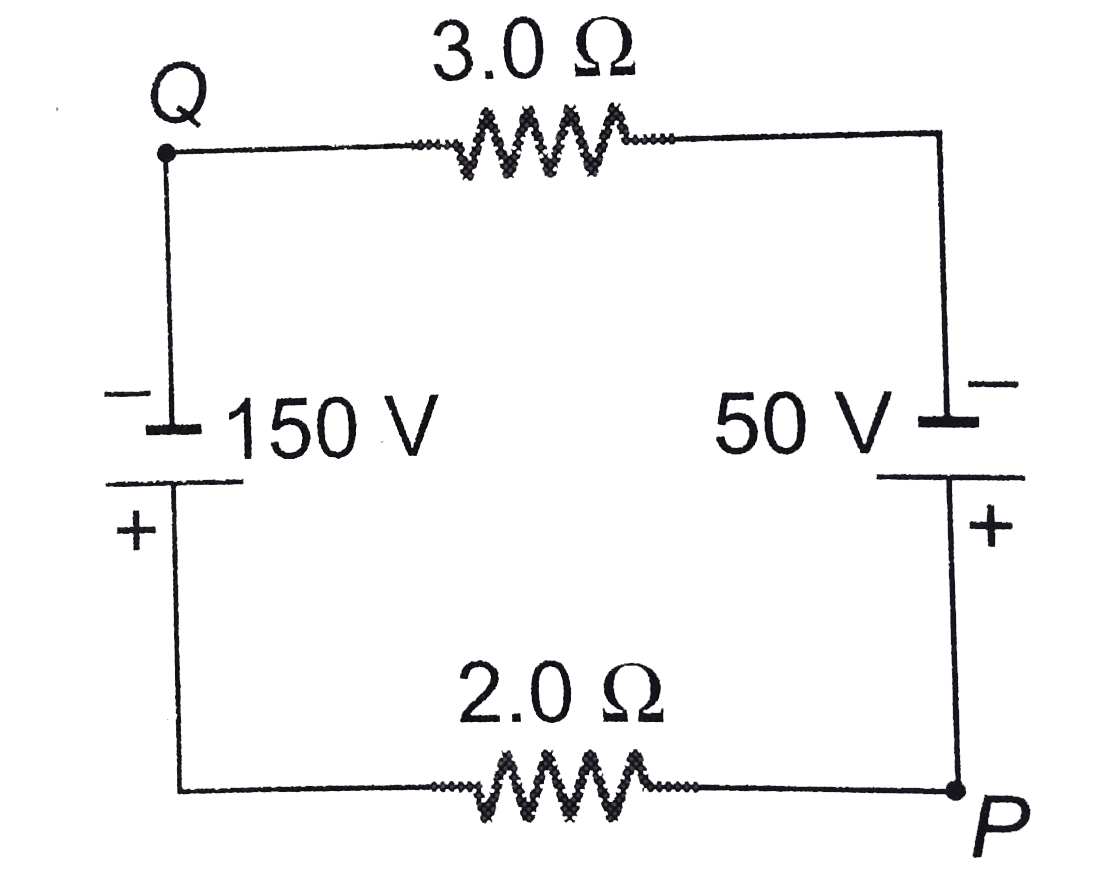
View SolutionIn Figure if the potential at Point P is 100V, what is the potential at point Q?
View SolutionHow much work is done in moving a charge of 5C across two points having a potential difference of 16V?
View SolutionFind the work done (in J) when a charge of 20 C moves across a potential difference of 4 V.
View Solution

