(a) Calculate the potential at a point P due to a charge of located 9 cm away.
(b) Hence obtain the work done in bringing a charge of from infinity to the point P. Does the answer depend on the path along which the charge is brought ?
To solve the given problem, we will break it down into two parts as specified in the question.
Part (a): Calculate the potential at point P
1. Identify the formula for electric potential (V):
The electric potential V at a distance R from a point charge Q is given by the formula:
V=14πϵ0QR
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
2. Convert the distance from cm to meters:
The distance R is given as 9 cm. We need to convert this to meters:
R=9cm=9100m=0.09m
3. Substitute the values into the formula:
The charge Q is given as 4×10−7C. Now substituting the values into the potential formula:
V=14π(8.85×10−12)4×10−70.09
4. Calculate the potential:
First, calculate the constant:
14πϵ0≈9×109N m2/C2
Now substituting this value:
V=9×109×4×10−70.09
V=9×109×49×10−2=4×104V
Part (b): Calculate the work done in bringing a charge from infinity to point P
1. Identify the formula for work done (W):
The work done W in bringing a charge q from infinity to a point where the potential is V is given by:
W=q⋅V
2. Substitute the values:
The charge q is given as 2×10−9C and the potential V we calculated in part (a) is 4×104V:
W=(2×10−9)×(4×104)
3. Calculate the work done:
W=8×10−5J
Conclusion on the path dependence
The work done in bringing the charge from infinity to point P does not depend on the path taken. This is because the work done depends only on the potential difference between the starting point (infinity) and the endpoint (point P), not on the specific path taken to get there.
Summary of the Solution
- Potential at point P: 4×104V
- Work done in bringing the charge: 8×10−5J
- Path dependence: The work done does not depend on the path taken.
The electric potential V at a distance R from a point charge Q is given by the formula:
V=14πϵ0QR
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/N m2.
The distance R is given as 9 cm. We need to convert this to meters:
R=9cm=9100m=0.09m
The charge Q is given as 4×10−7C. Now substituting the values into the potential formula:
V=14π(8.85×10−12)4×10−70.09
First, calculate the constant:
14πϵ0≈9×109N m2/C2
Now substituting this value:
V=9×109×4×10−70.09
V=9×109×49×10−2=4×104V
The work done W in bringing a charge q from infinity to a point where the potential is V is given by:
W=q⋅V
The charge q is given as 2×10−9C and the potential V we calculated in part (a) is 4×104V:
W=(2×10−9)×(4×104)
W=8×10−5J
The work done in bringing the charge from infinity to point P does not depend on the path taken. This is because the work done depends only on the potential difference between the starting point (infinity) and the endpoint (point P), not on the specific path taken to get there.
- Potential at point P: 4×104V
- Work done in bringing the charge: 8×10−5J
- Path dependence: The work done does not depend on the path taken.
Similar Questions
If the work done in bringing a charge of 10−18C from infinity to point P is 2×10−17 J , what is the electric potential at P?
View SolutionThe work done in carrying a point charge form one point to another in an electrostatic field depends on the path along which the point charge is carried.
View Solution
Knowledge Check
The potential at a point due to charge of 5×10−7C located 10 cm away is
A3.5×105VB3.5×104VC4.5×104VD4.5×105VThe potential at a point due to charge of 5×10−7C located 10 cm away is
In the above question work done in bringing a charge of 4×10−9C from infinity to that point isA2.4×10−4JB1.8×10−4JC3.2×10−5JD4.1×10−5JIn the question number 4, work done in bringing a charge of 4×10−9 C form infinity to that point is
A2.4×10−4JB1.8×10−4JC3.2×10−5JD4.1×10−5J
The work done in bringing 5 C of charge from infinity to a point A near a charged body is 20 J. Find the potential at point A.
View SolutionThe work done in moving a charge of 2×10−9 C from a point of potential - 3000 V to another point P is 5×10−5J . Find the potential at the point P.
View SolutionThe potential at a point is 20 V. The work done in bringing a charge of 0.5 C. from infinity to this point will be
View SolutionCalculate the work done in taking a charge −2×10−9C from A to B via C (in diagram )
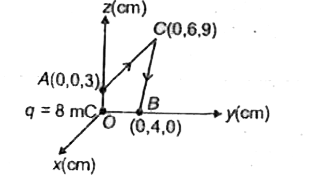
View SolutionIf 6W is the work done in bringing a infinitesimal small test charge 6g from infinity to a point P, then potential at point P is
View Solution

