A thin hoop of weight and radius rest on a rought inclined plane as shown in the figure. The minimum coefficient of friction needed for this configuration is.
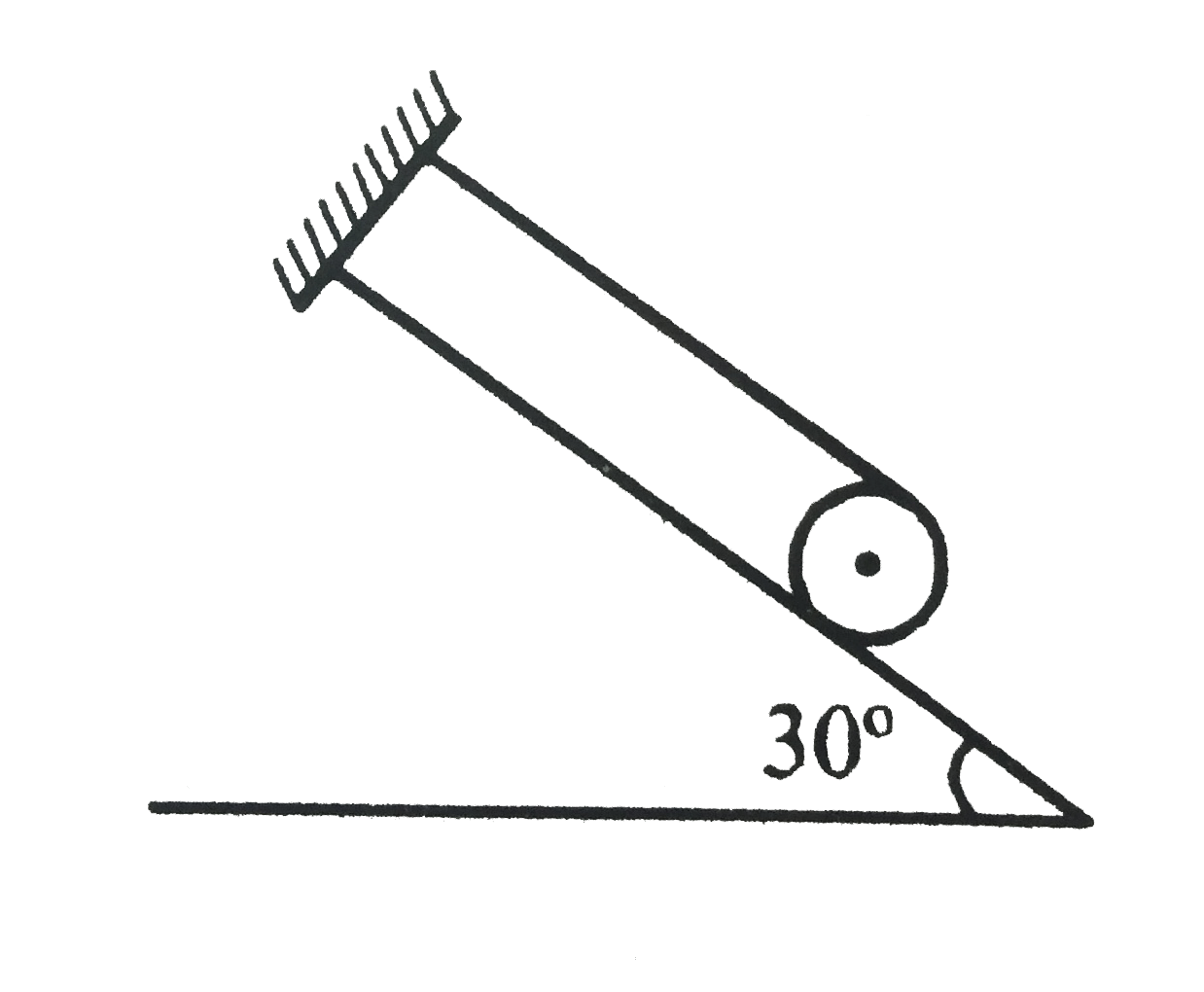 .
.
The correct Answer is:D
Taking translational equilibrium along plane.
….(1)
Taking translating equilibrium to the plane
…(2)
For rotational equilibrium about centre of mass
....(3)
From (1) and (3)
....(4)
From (2) and (4)
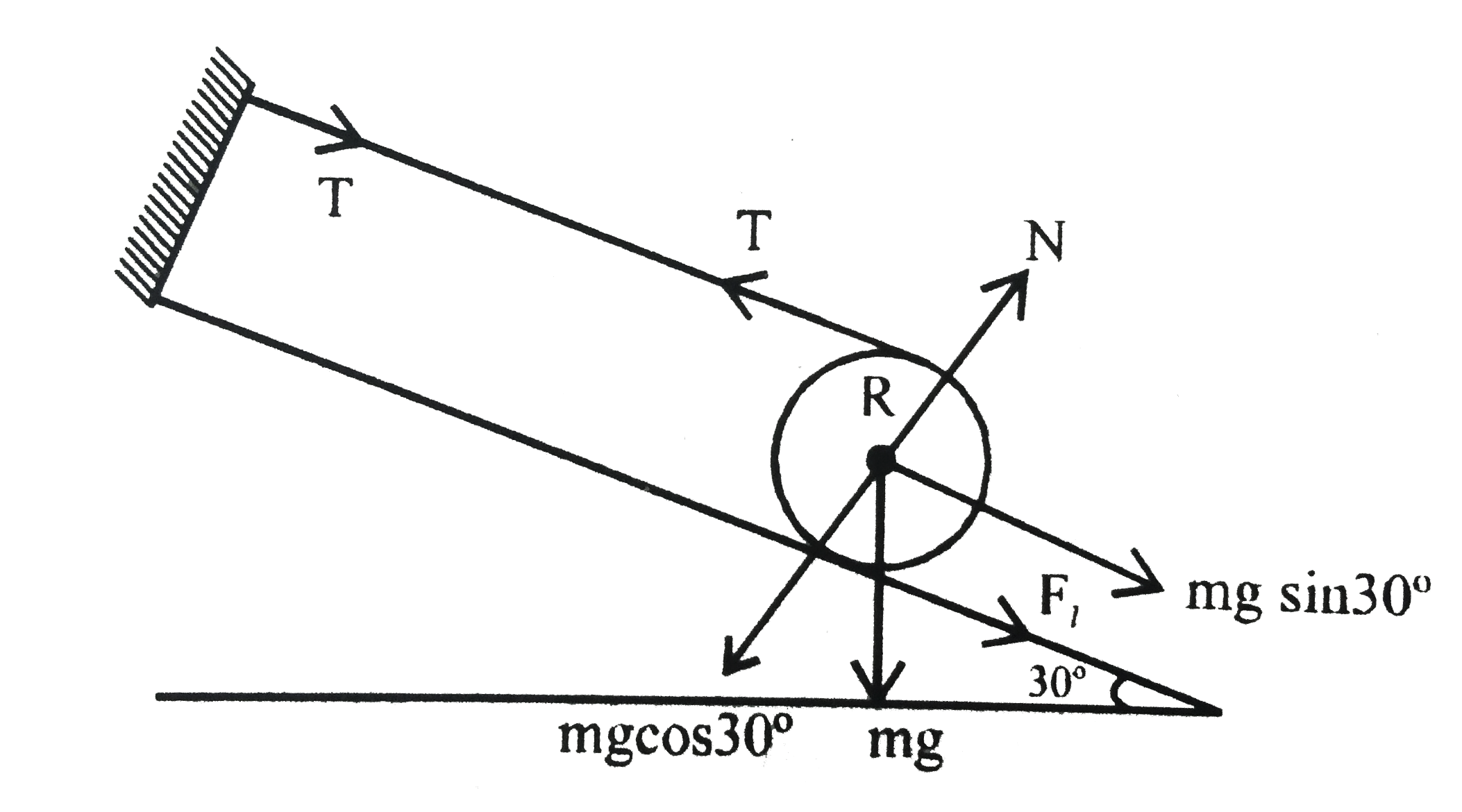
.
Similar Questions
A solid cylinder of mass m is wrapped with an inextensible light string and, is placed on a rough inclined plane as shown in the figure. The frictional force acting between the cylinder and the inclined plane is :
 [The coefficient of static friction, μs is 0.4]
[The coefficient of static friction, μs is 0.4]
View SolutionA cube of weight 10N rests on a rough inclined plane slope 3/5. The coefficient of friction is 0.6. The minimum force necessary to start the cube moving up the plane is
View Solution
Knowledge Check
A solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
Africtional force is always μmgcosθBfriction is a dissipative forceCby decreasing θ, frictional force decreasesDfrictiona opposes translation and supports rotation.A cube of weight 10N rests on a rough inclined plane of slope 3 in 5. The coefficient of friction is 0.6. The minimum force necessary to start the cube moving up the plane is
A5.4NB10.8NC2.7ND18NA sphere of weight W=100N is kept stationary on a rough inclined plane by a horizontal string AB as shown in figure. Then :
 Atension in th string is 100 NBnormal reaction on the sphere by the plane is 100 NCtension in the string is 1002+√3NDfore of friction on the sphere I 1002+√3N
Atension in th string is 100 NBnormal reaction on the sphere by the plane is 100 NCtension in the string is 1002+√3NDfore of friction on the sphere I 1002+√3N
A solid sphere is released from the state of rest on an inclined plane. Mass of the sphere is m and its radius is r. Inclined plane makes an angle with the horizontal. If minimum coefficient of friction required for pure rolling is n7tanθ then calculate value of n.
View SolutionA block of mass m=2kg is resting on a inclined plane of inclination 30∘ as shown in figure The coefficient of friction between the block and the plane is μ=0.5 what minimum force F (in newton) should be applied perpendicular to the plane on the block so that the does not slip on the plane?

View SolutionA block of mass m = 4 kg is placed over a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is u=0.5. A force F= 10 N is applied on the block at an angle of 30°. The friction force between the block and wedge is

View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
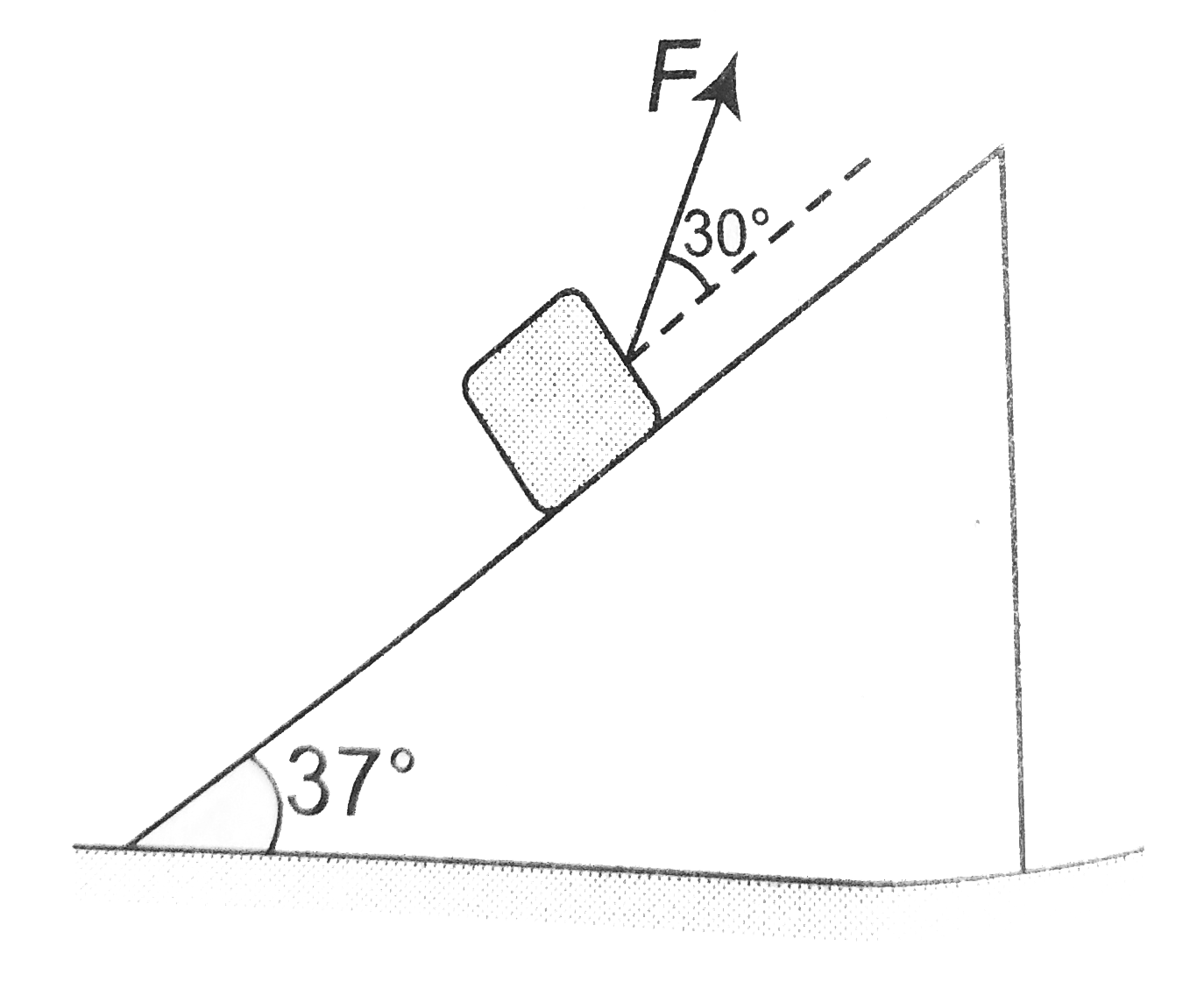
View SolutionA uniform chain is placed at rest on a rought surface of base length 1 and height h on an irregular suface as shown in figure Then the minimum coefficient of friction between the chain and the surface must be equal to
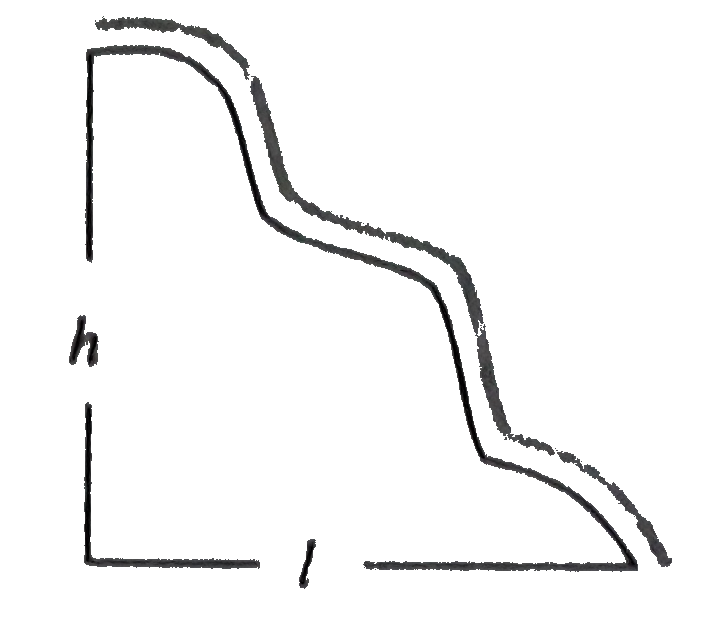
View Solution
