A uniform chain is placed at rest on a rought surface of base length 1 and height h on an irregular suface as shown in figure Then the minimum coefficient of friction between the chain and the surface must be equal to
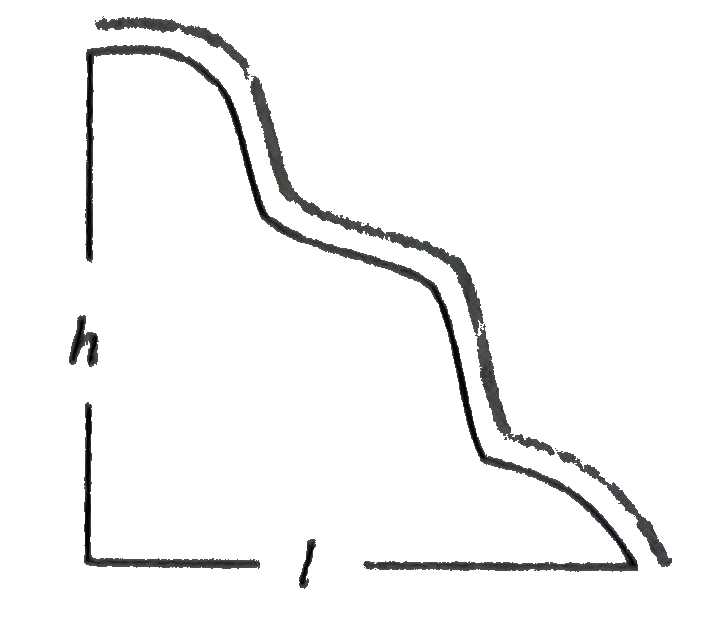
μ=h2l
μ=ht
μ=3h2l
μ=2h3l
The correct Answer is:b
For equilibrium
∫μdmgcosθ≥∫dmgsinθ
∫μλdlgcosθ≥∫λdlgsinθ
μ∫dlcosθ≥∫dlsinθ(∵sinθ=dydt,cosθ=dxdt)
μ∫dx≥∫dyorμi≥h
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A uniform solid sphere rolls down a vertical surface without sliding. If the vertical surface moves with an acceleration a=g/2, find the minimum coefficient of friction between the sphere and vertical surfaces so as to prevent relative sliding.

View SolutionA chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
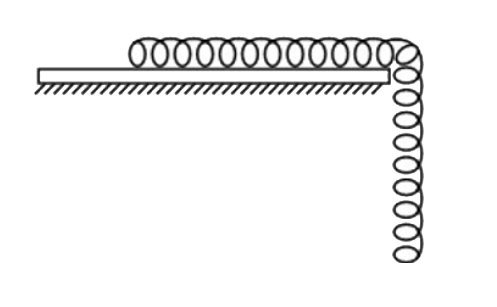
View Solution
Knowledge Check
A block of mass 1 kg is placed on a wedge shown in figure. Find out minimum coefficient of friction between wedge and block to stop the block on it.
 A0.6B0.9C1D0.2
A0.6B0.9C1D0.2A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
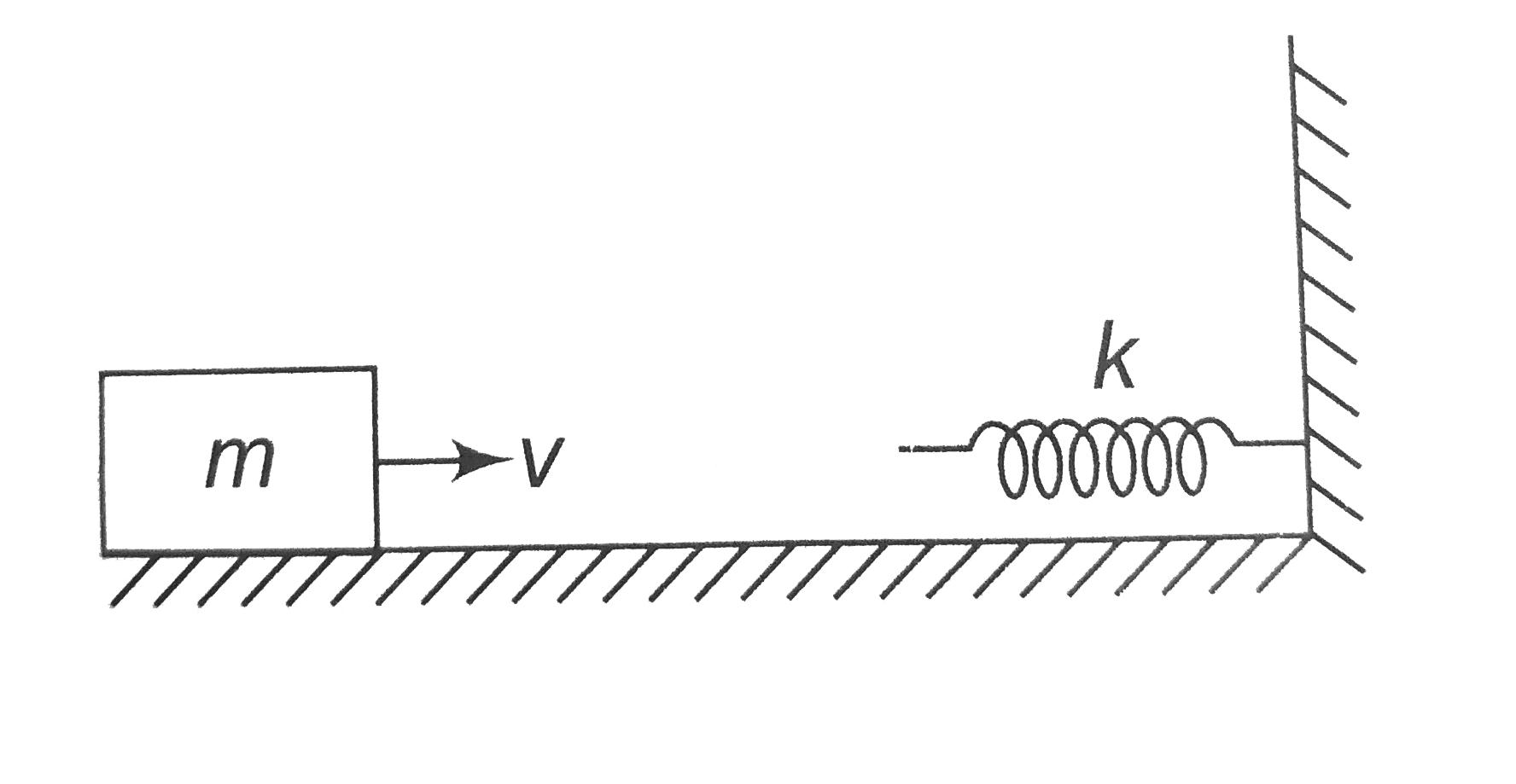 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2A uniform ring placed on a rough horizontal surface is given a sharp impulse as shown in the figure-5.130. As a consequence, it acquires a linear velocity of 2m/s. If coefficient of friction between the ring and the horizontal surface is 0.4 :
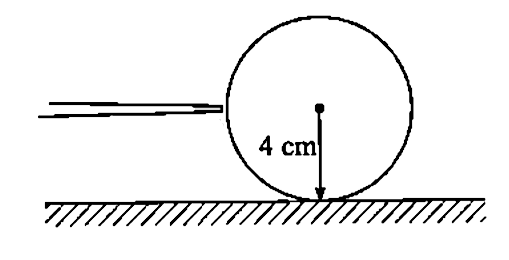 ARing wil lstart pure rolling afler O.25sBWhen ring will start pure rolling its .velocity is 1m//sCAfter 0.5s from impulse its velocity is 1m//s.DAfter0.125 s from impulse its velocity is 1m//s.
ARing wil lstart pure rolling afler O.25sBWhen ring will start pure rolling its .velocity is 1m//sCAfter 0.5s from impulse its velocity is 1m//s.DAfter0.125 s from impulse its velocity is 1m//s.
A uniform ring of mass m is placed on a rough horizontal fixed surface as shown in the figure. The coefficient of friction between the left part of the ring and left part of the horizontal surface is μ1=0.6π and between right half and the surface is μ2=0.2π. At the instant shown, now the ring has been imparted an angular velocity in clockwise sense in the figure shown. At this moment magnitude of acceleration of centre O of the ring (in m/s2) is (take g=10m/s2)

View SolutionA uniform chain of length L is lying partly on a table, the remaining part hanging down from the edge of the table. If the coefficient of friction between the chain and the table is 0.5 what is the minimum length of the chain that should lie on the table, to prevent the chain from slipping down to the ground.
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
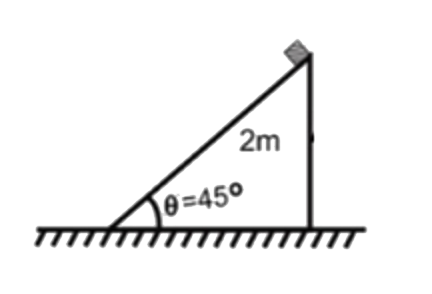
View SolutionA uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then

View SolutionA thin hoop of weight 500N and radius 1m rest on a rought inclined plane as shown in the figure. The minimum coefficient of friction needed for this configuration is.
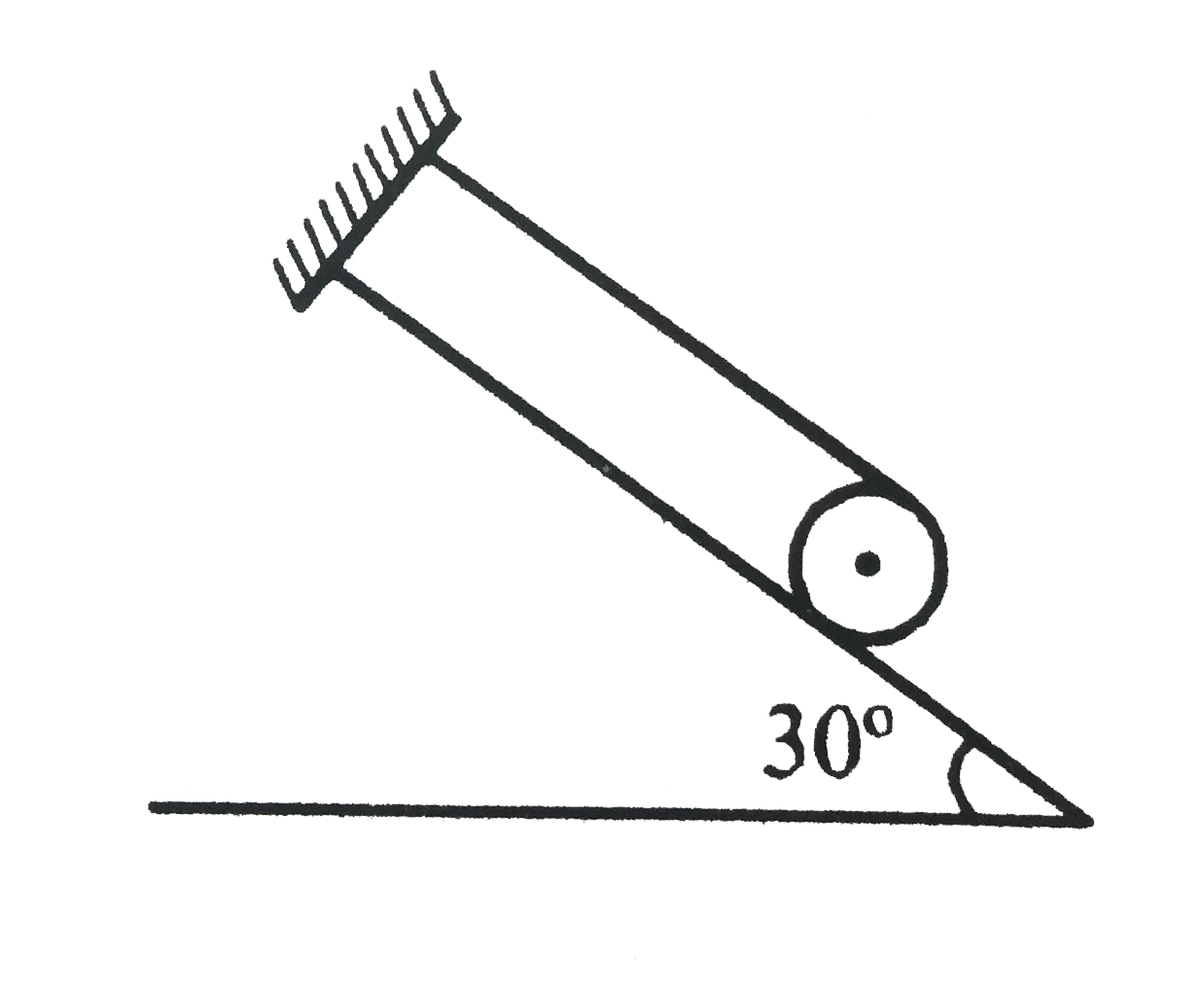 .
.
View Solution
