In the LR circuit shown, what is the variation of the current I as a function of time? The switch is closed at time t=0 sec.
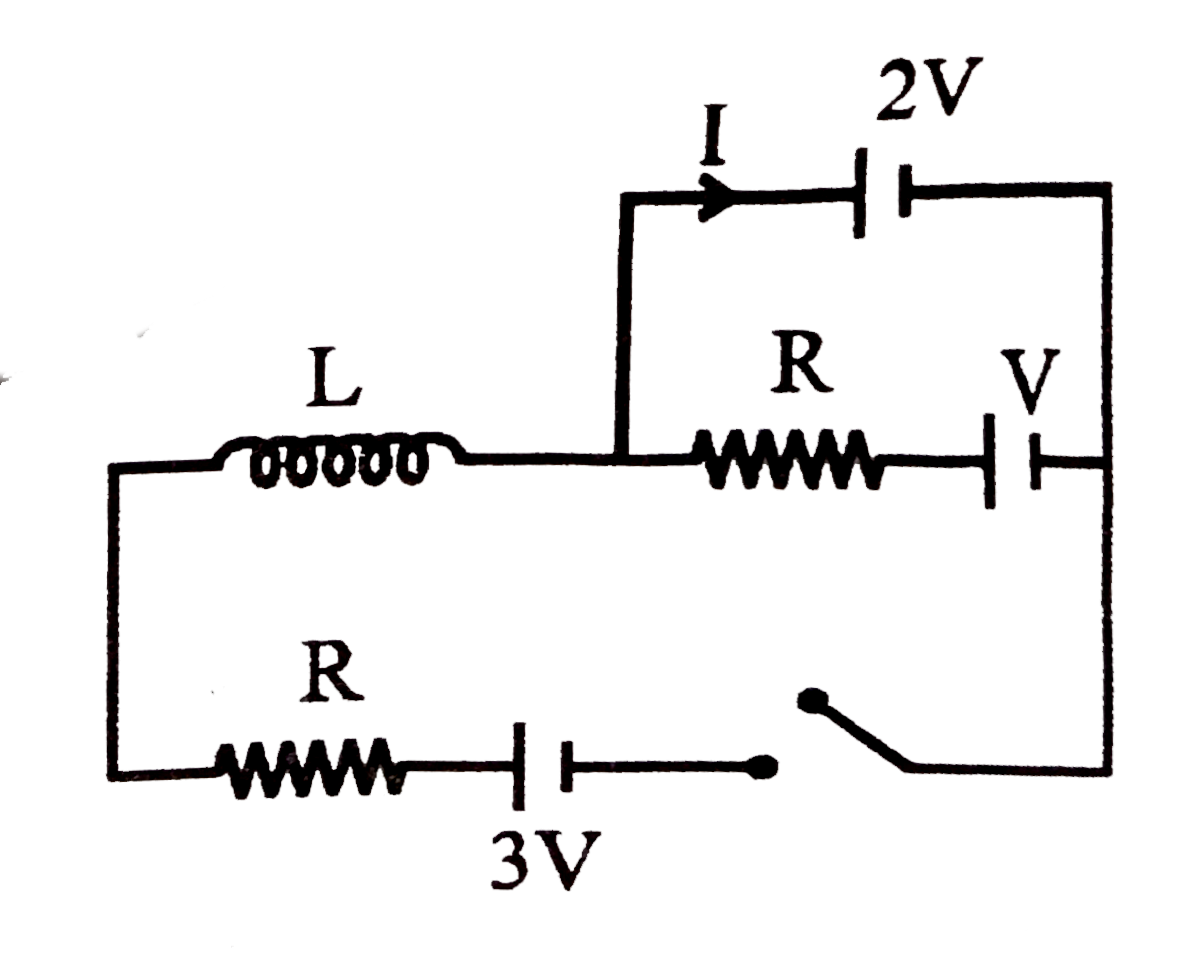
The correct Answer is:−VRe−RtL
Applying loop law for CE2DC
−2V+V+I2R=0⇒I2=VR…(1)
Applying loop law for ABCDE
−LdI1dt−2V+3V−I1R=0

LdI1dt+I1R=V
I1=VR(1−e−Rt/L)…(2)
Applying junction law at C
I1=I+I2⇒I=I1−I2=−VRe−(R/L)t
Similar Questions
In the circuit shown in figure-5.115, find the current in inductor as a function of time if switch is closed at t=0.
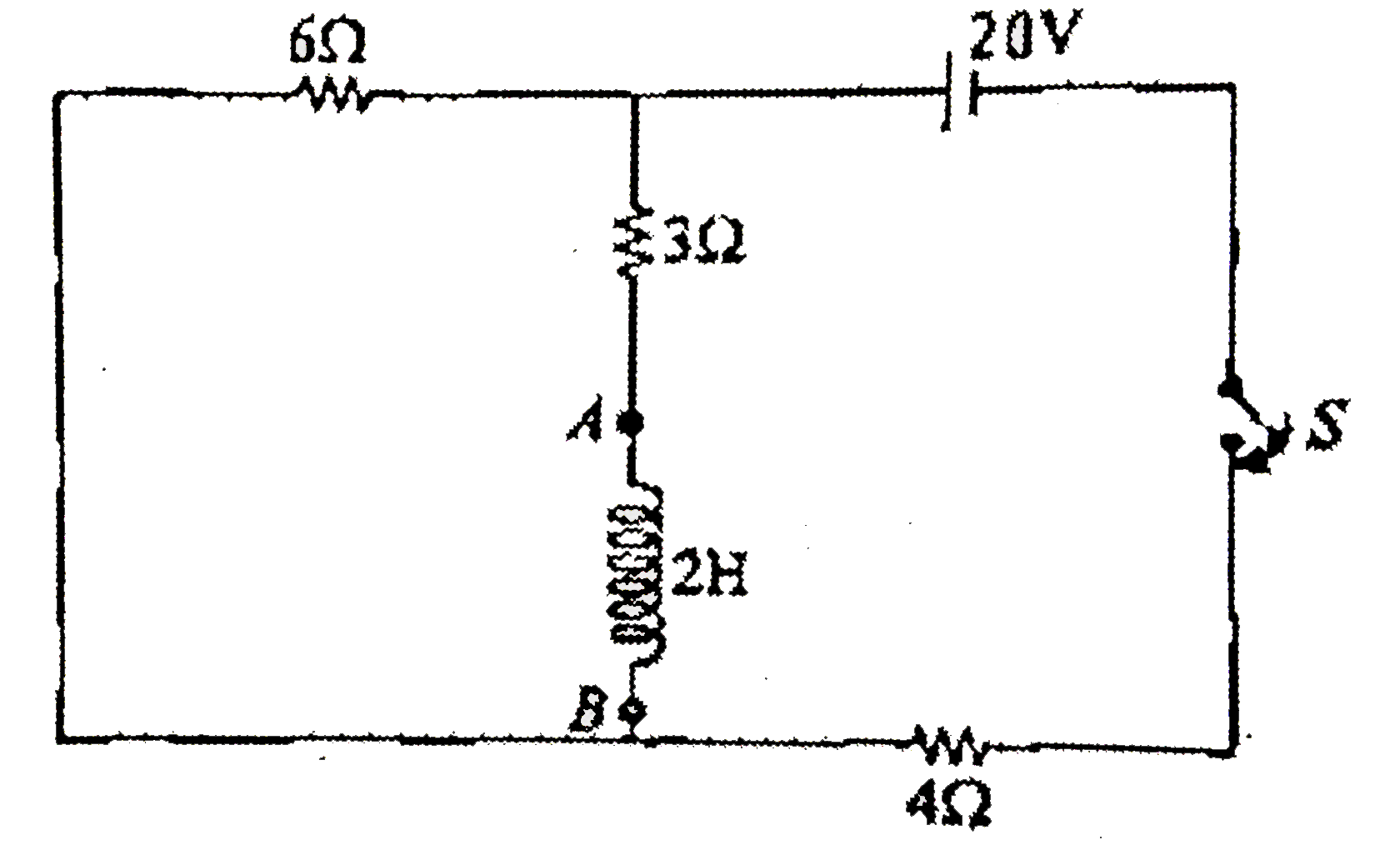
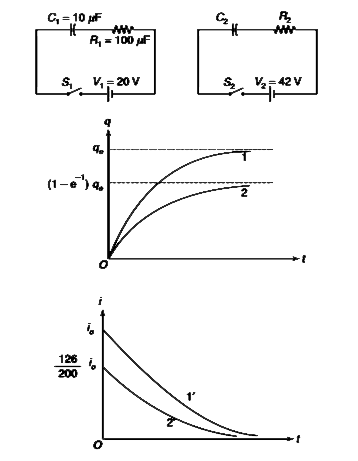
View SolutionConsider two circuits given below. When switches S1andS2 are closed at t=0, the charge on capacitors C1 and C2 change with time as shown in graph 1 and 2 respectively. The current i1 and i2 in the two circuits change as shown in graph 1' & 2' respectively. Write the variation of current in the second circuit as function of time after the switch is closed at t=0.e−1=0.37
View Solution
Knowledge Check

In given LR circuit the switch S is closed at time t=0 thenAThe ratio of induced emfs in the inductors of inductance L and 2L will be constantBThe ratio of induced emfs in the inductor of inductance L and 2L will be time varyingCthe potential difference VA−VB increases with timeDThe potential difference VA−VB will be constantIn the circuit shown, the switch is closed at t=0, the currents I1,I2 and I3 are
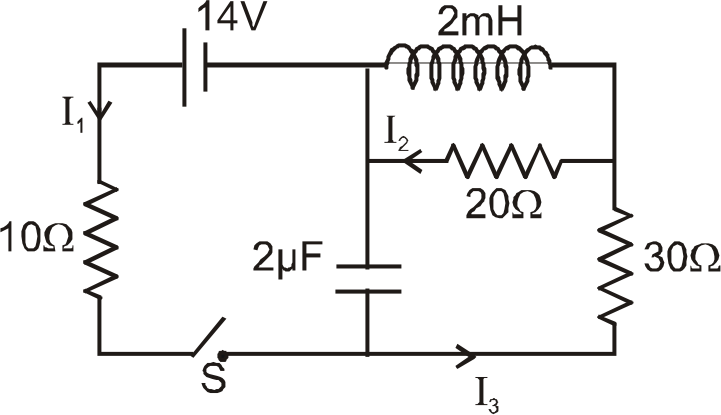 A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6A
A1.4A,0,0B1.4 A,0.70 A,0.70 AC0,0,0D1.2A,0.6A,0.6AConsider the circuit shown in figure. The current through the battery a long time after the switch S is closed is:
 AER1BER2CER1+R2DE(R1+R2)(R1R2)
AER1BER2CER1+R2DE(R1+R2)(R1R2)
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.
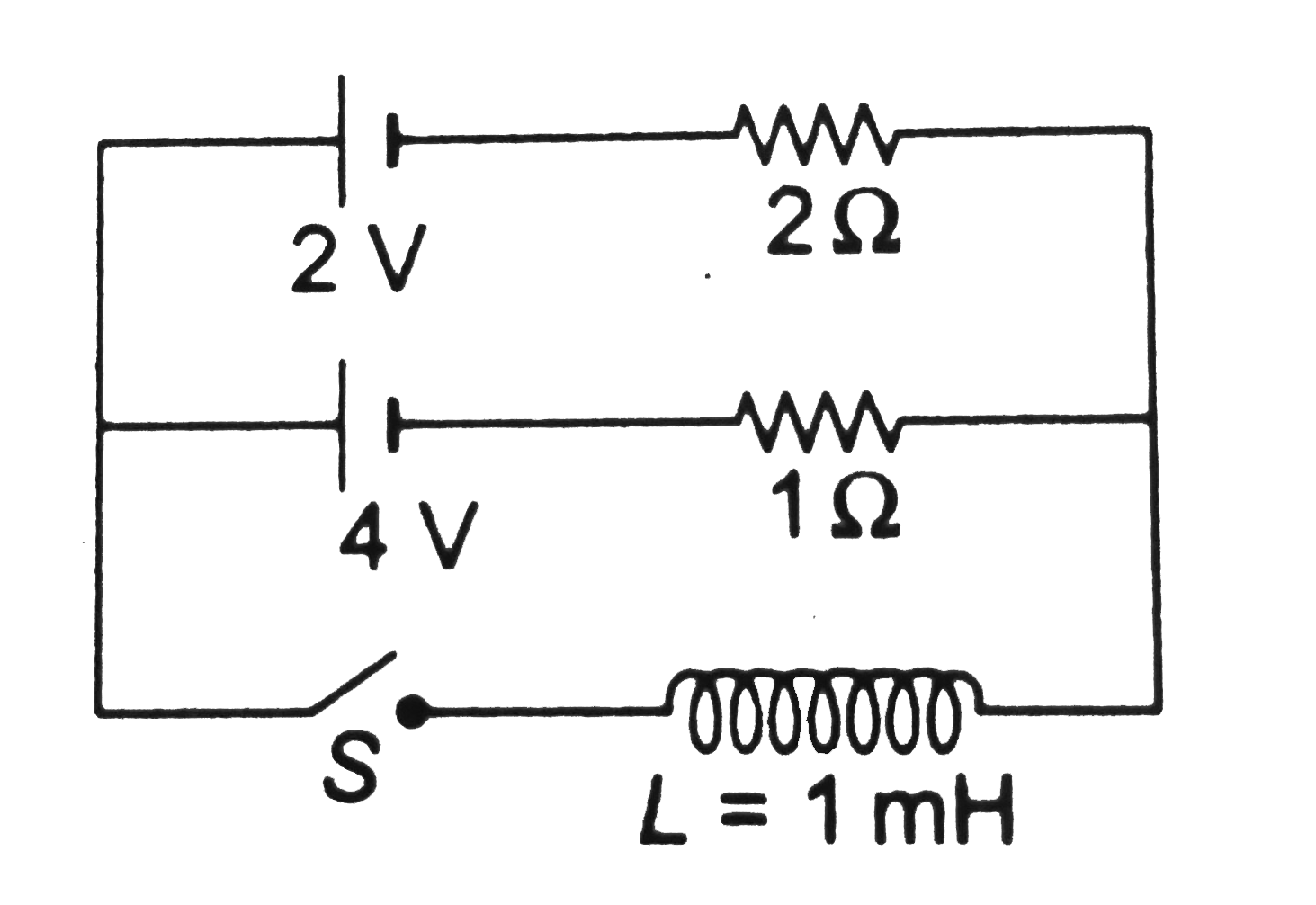
View SolutionIn the circuit diagram shown, intially there is no energy in the inductor and the capacitor. The switch is closed at t=0 . Find the current I as a function of time t .
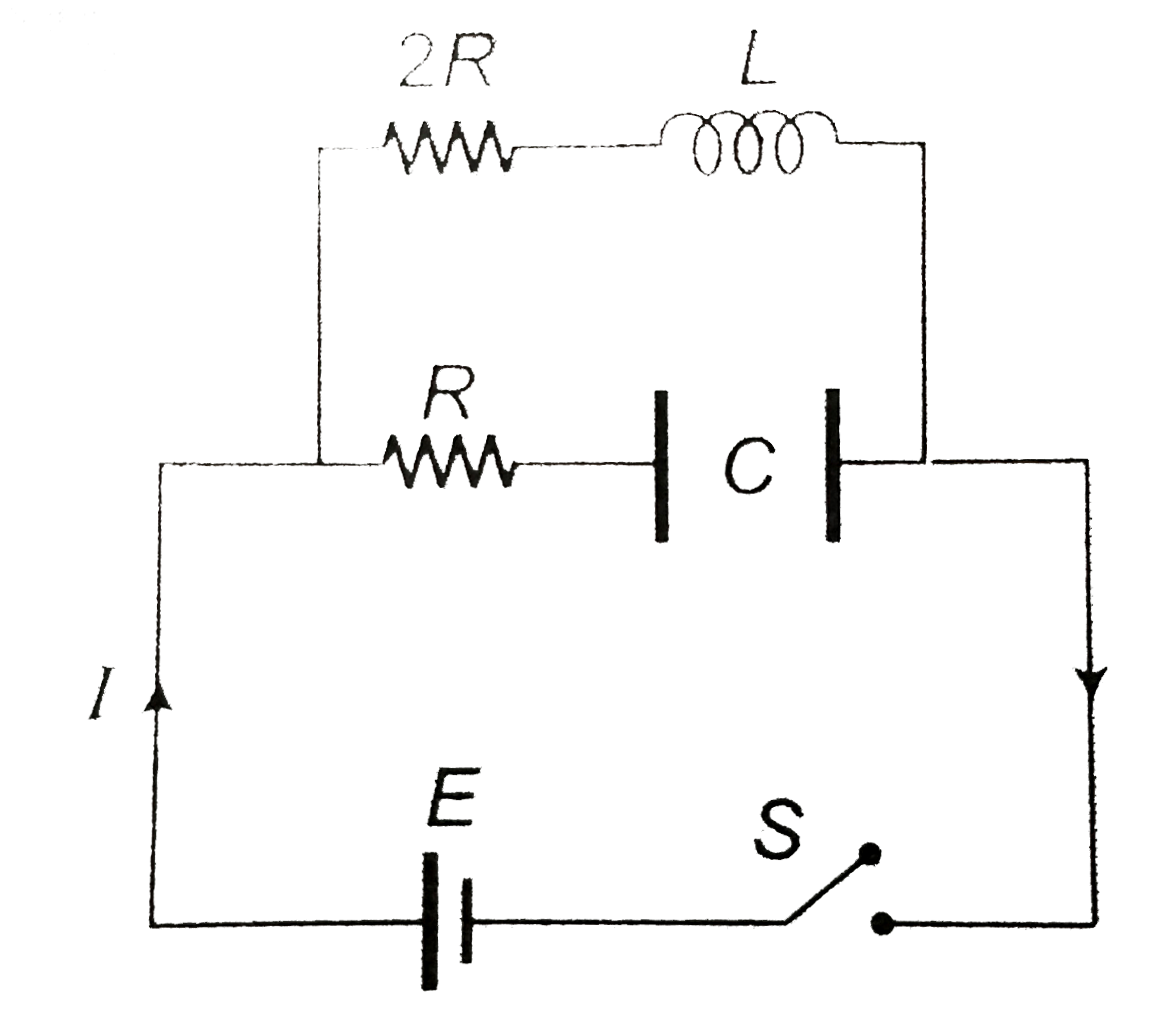
View SolutionIn the circuit shown, the switch ‘S’ has been closed for a long time and then opens at t = 0.
(a) Find the current through the inductor just before the switch is opened.
(b) Find the current I a long time after the switch is opened.
(c) Find current I as a function of time after the switch is opened. Also write the current through the cell as a function of time.
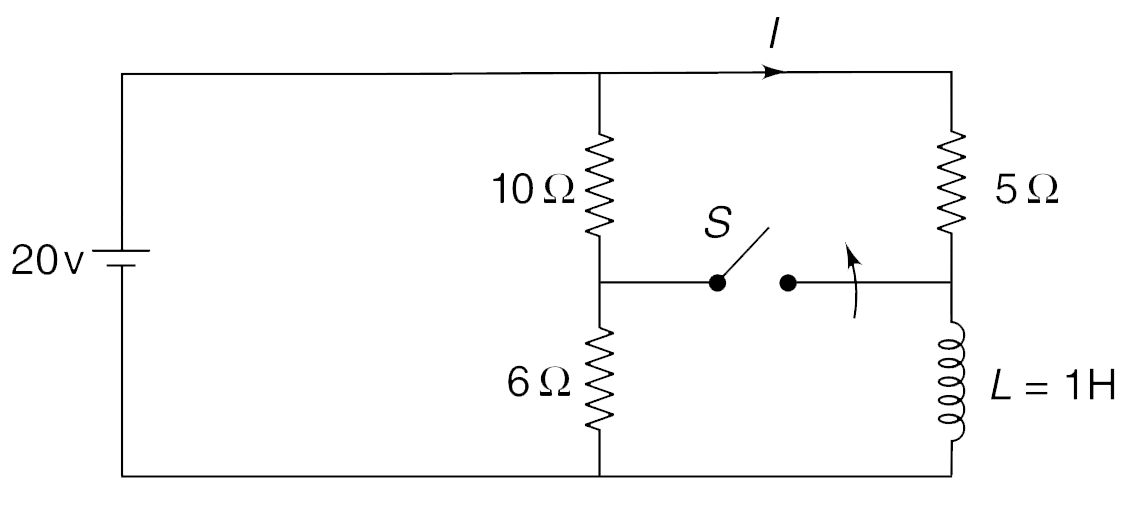
View SolutionIn the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
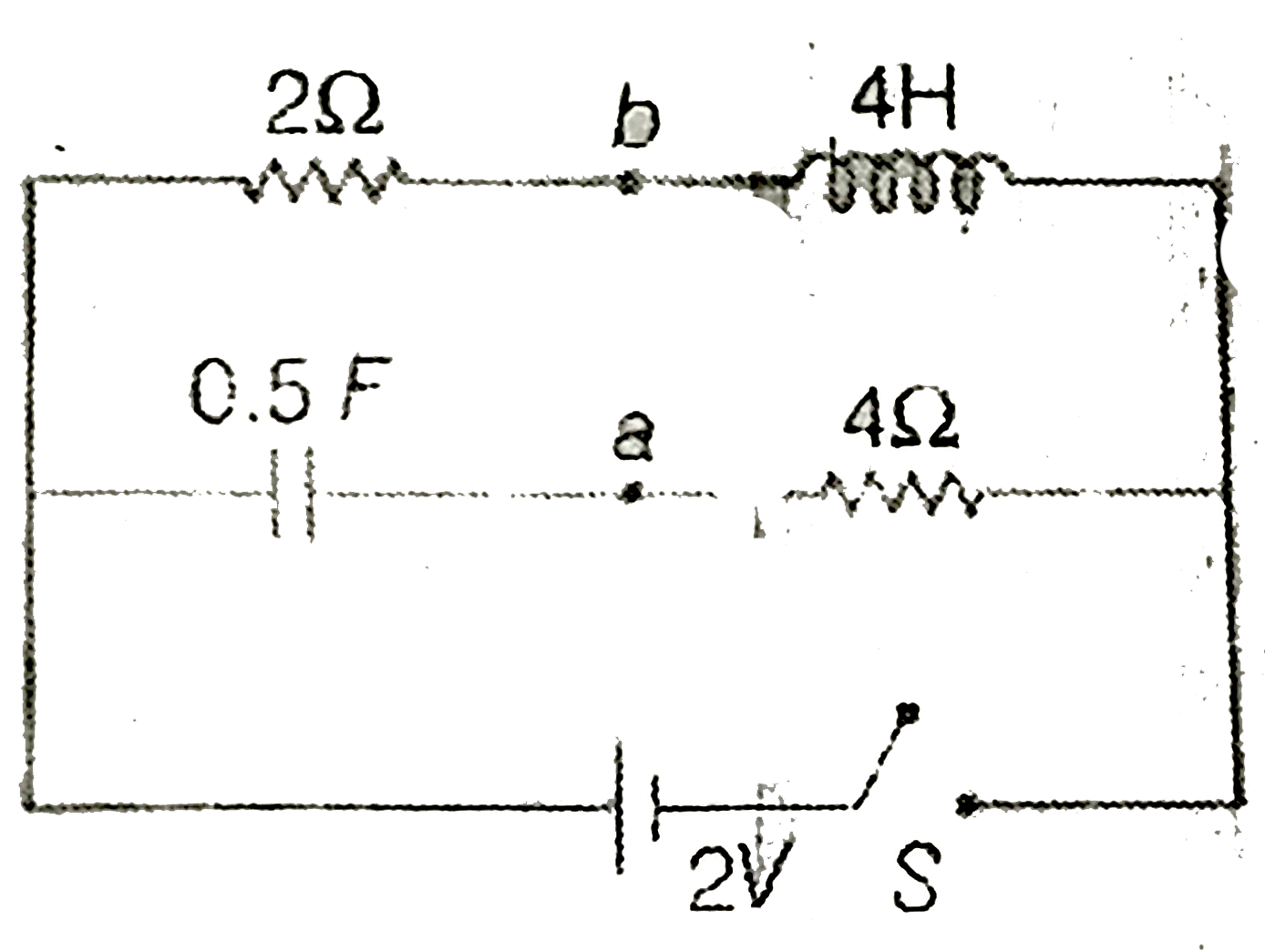
View SolutionIn the circuit as shown in figure the switch is closed at t=0.

At the instant of closing the switch
View Solution

