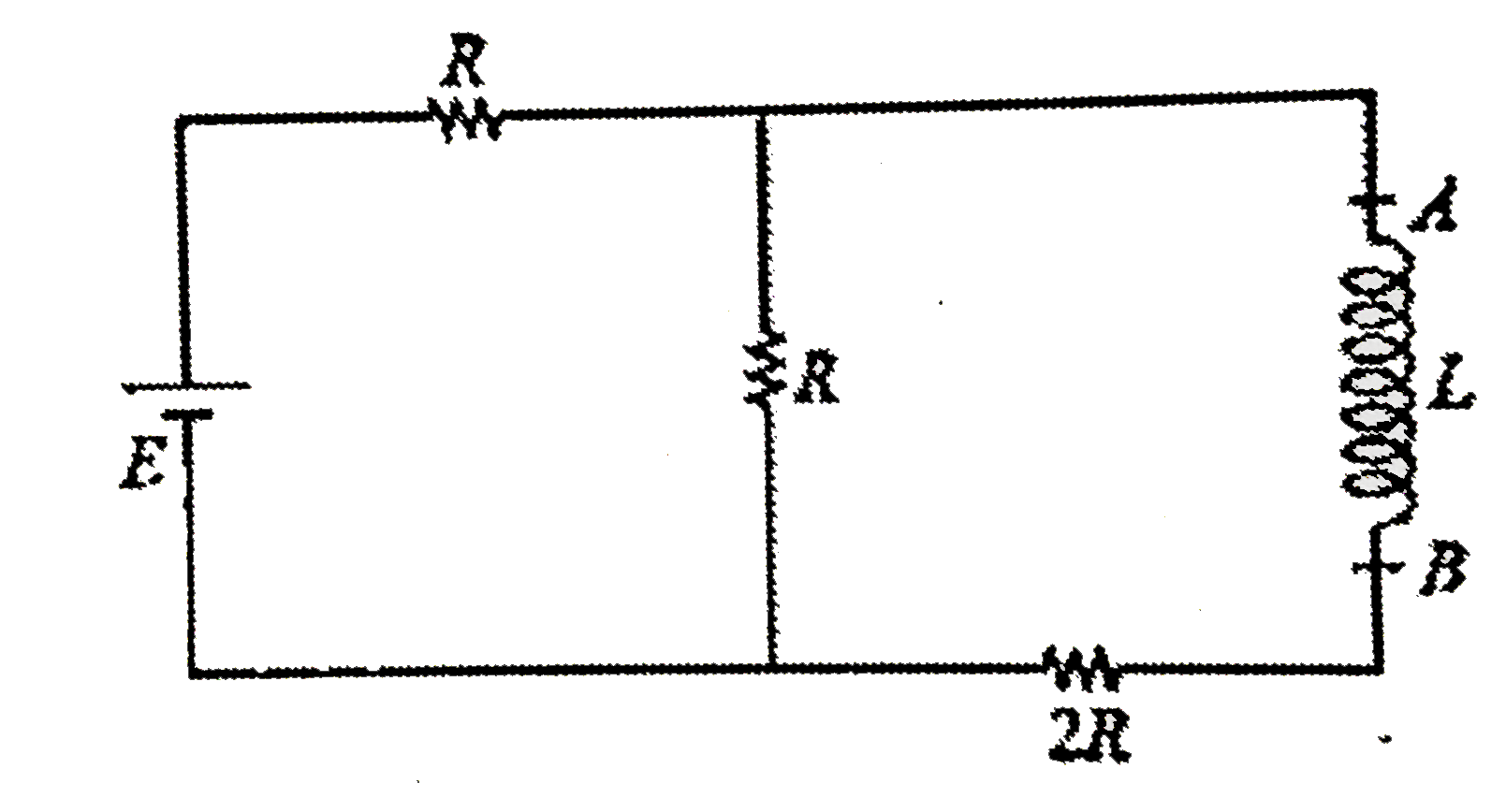
At , switch is closed. Find time constant of the circuit and current through inductor as a function of time .

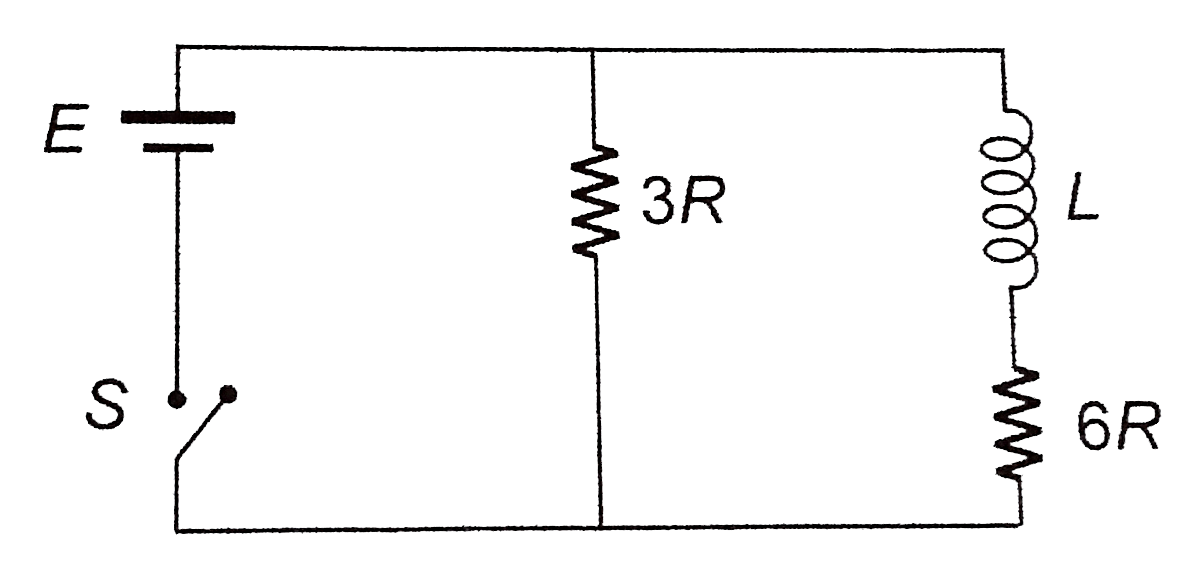
To determine time constant, first find equivalent resistance across by short-circuiting the battery,
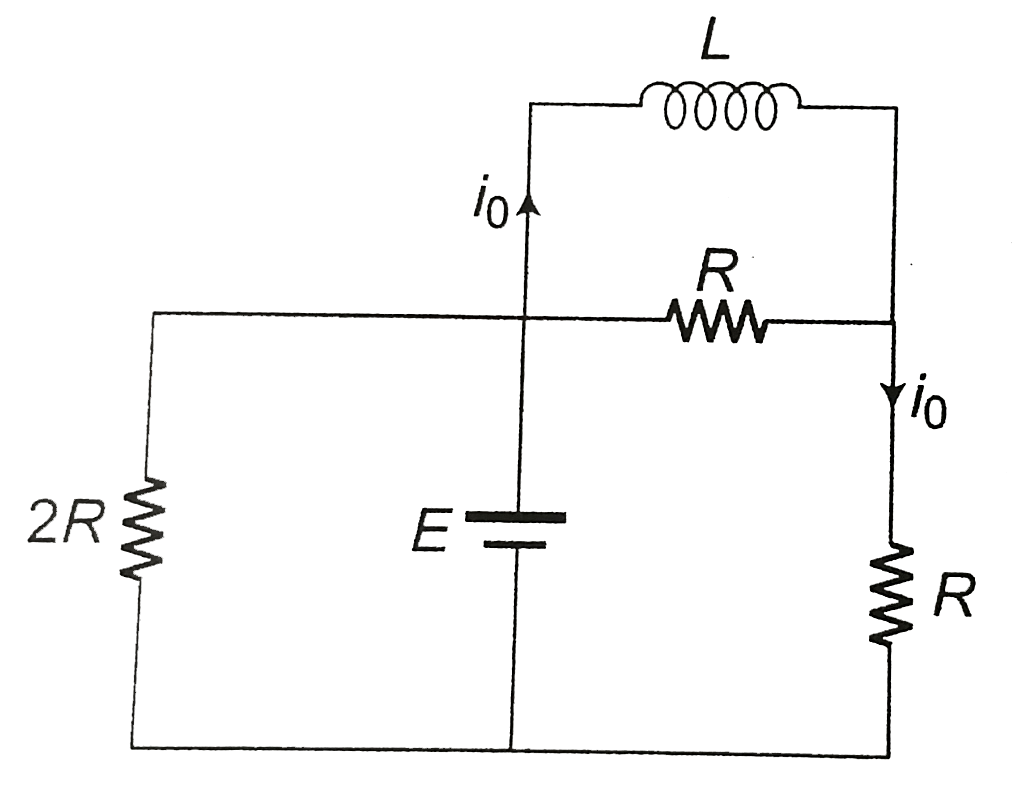
To determine current through inductor, first determine current in inductor in steady state and then
(a)
In steady-state, inductor offers zero resistance
(b)
In steady offer zero resistance
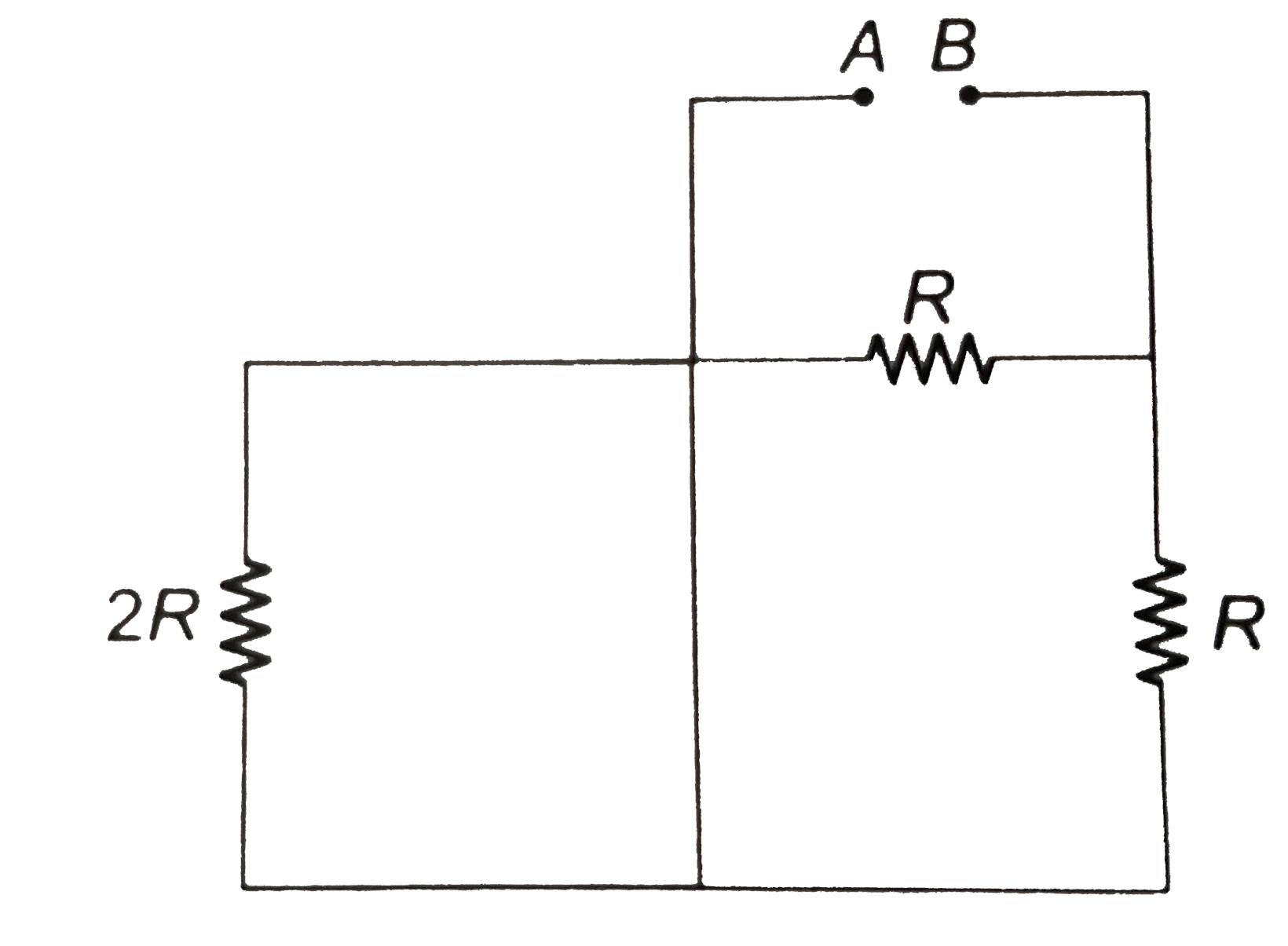
Here two brancges are parallel and independent.
 ltbgt
ltbgt 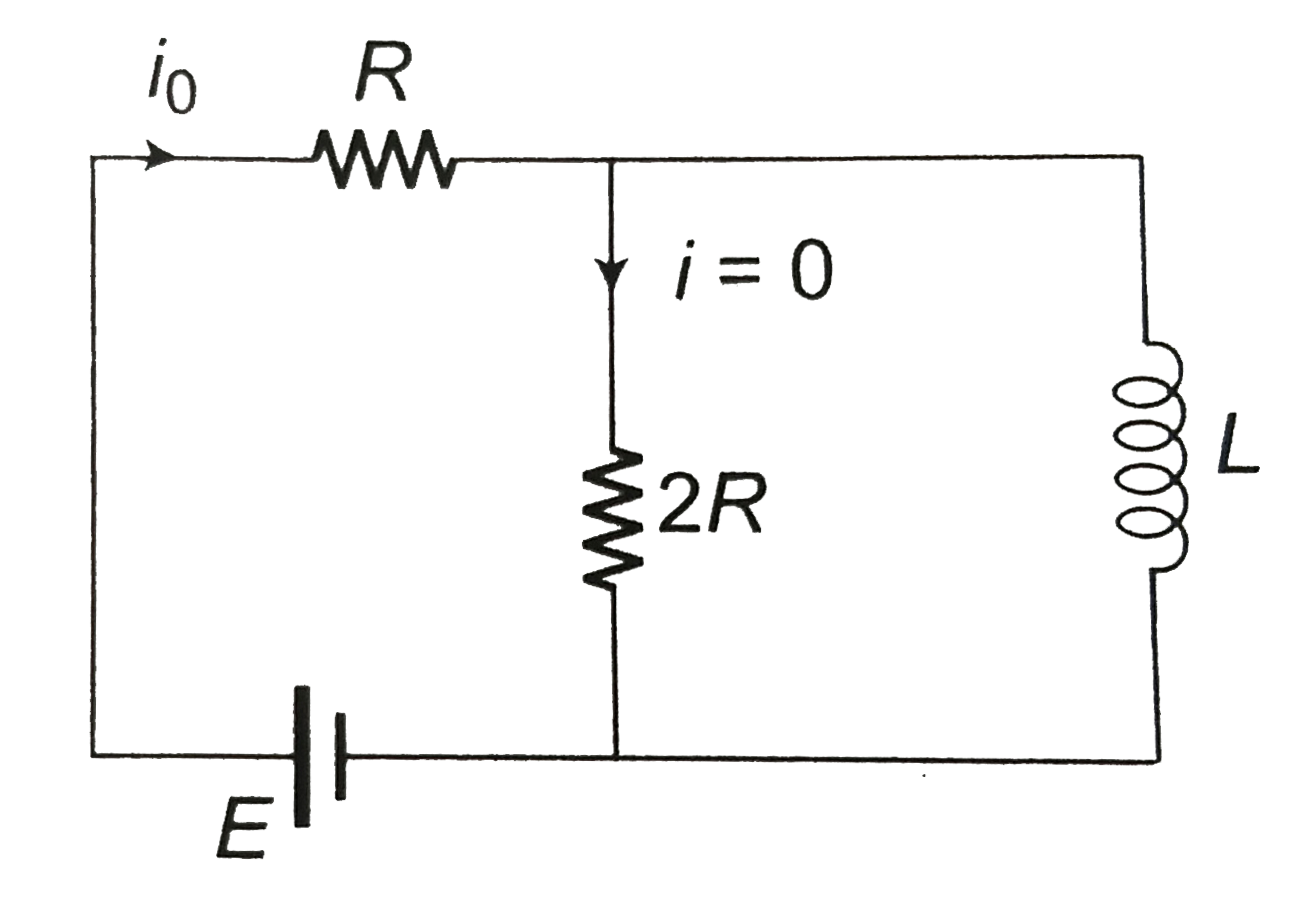

Topper's Solved these Questions
Similar Questions
In the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

View SolutionIn the circuit shown in the figure, switch S is closed at time t=0.
(a) Write current in the circuit and charge on capacitor as a function of time. Draw the graphical plot for the same.
(b) Find maximum charge on the capacitor. What is potential difference across the inductor when charge on the capacitor is maximum?
View Solution
Knowledge Check
In the circuit shown in figure switch S is closed at time t=0

Takin left to right current through the indcutor as apositive current, current through inductor varies with time asA B
B C
C D
D
In the following circuit the switch is closed at t=0.Intially there is no current in inductor.Find out current the inductor coil as a function of time.
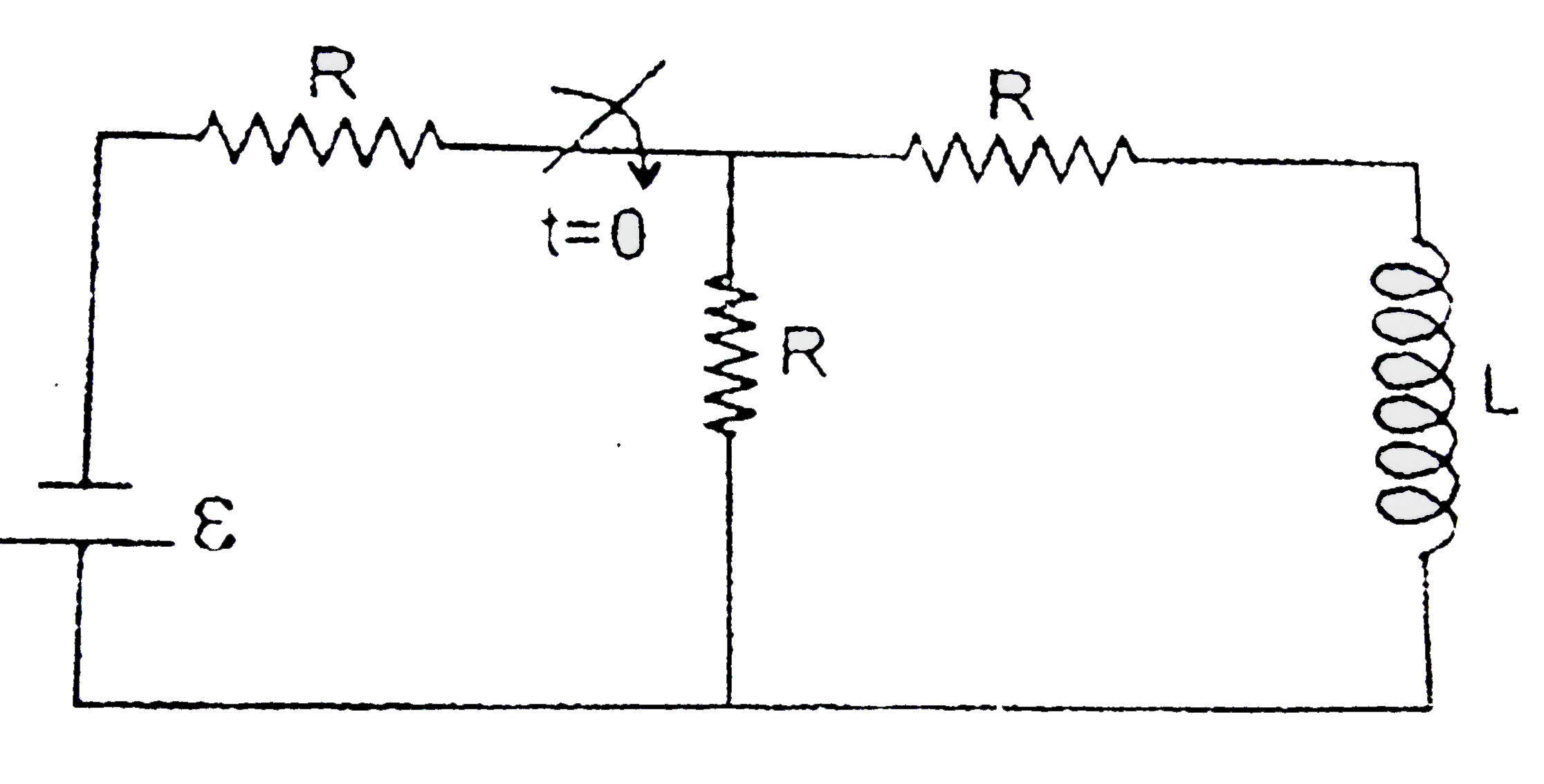
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View SolutionThe switch in figure is closed at time t=0. Find the current in the inductor and the current through the switch as functions of time thereafter.
View SolutionIn Fig. 30-44, after switch S is closed at time t = 0, the emf of the source is automatically adjusted to maintain a constant current i through S. (a) Find the current through the inductor as a function of time. (b) At what time is the current through the resistor equal to the current through the inductor?

View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t

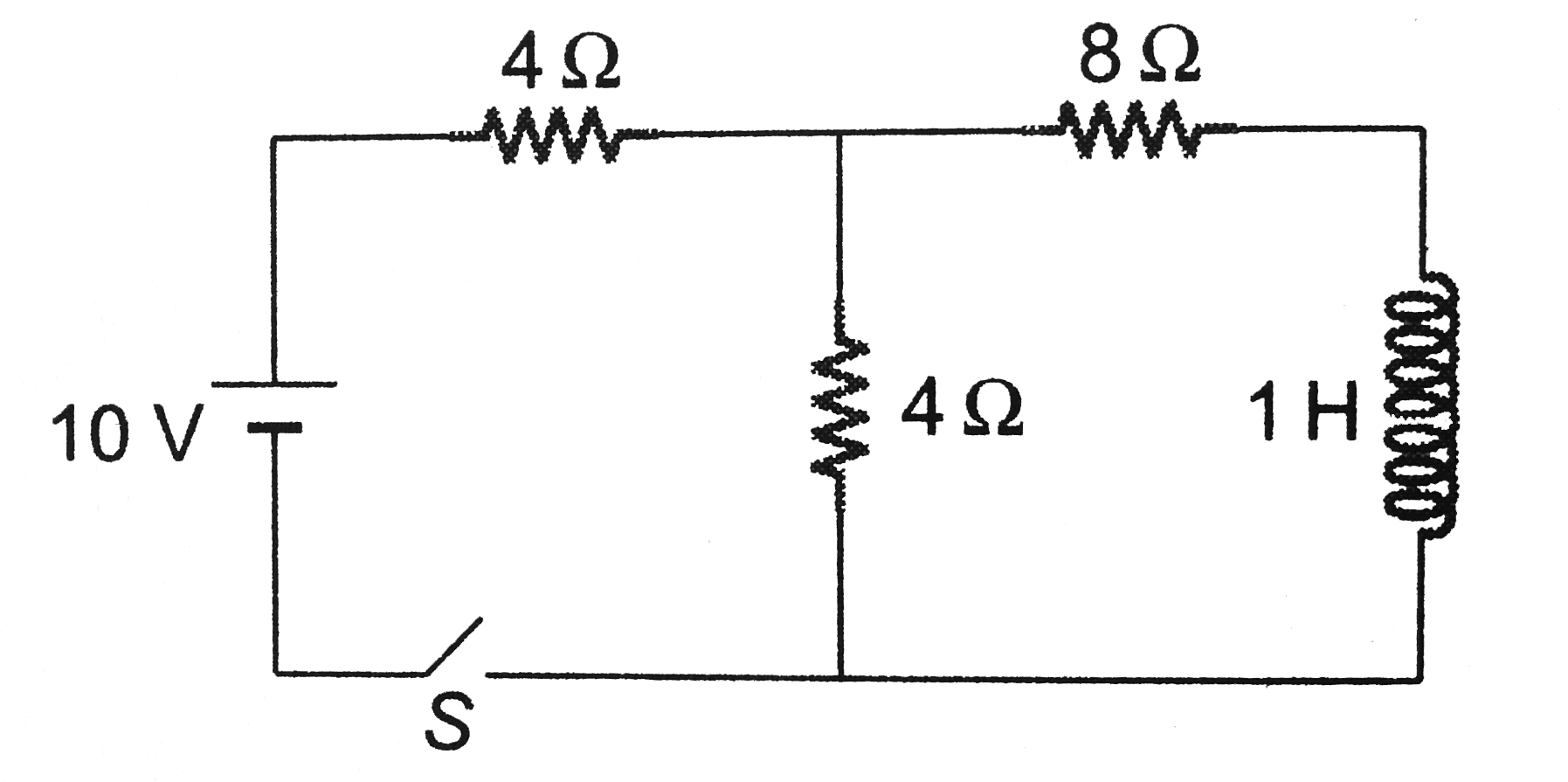
View SolutionIn the circuit arrangement shown in figure, the switch S is closed at t=0. Find the current in the inductance as a function of time? Does the current through 10Ω resistor vary with time or remains constant.
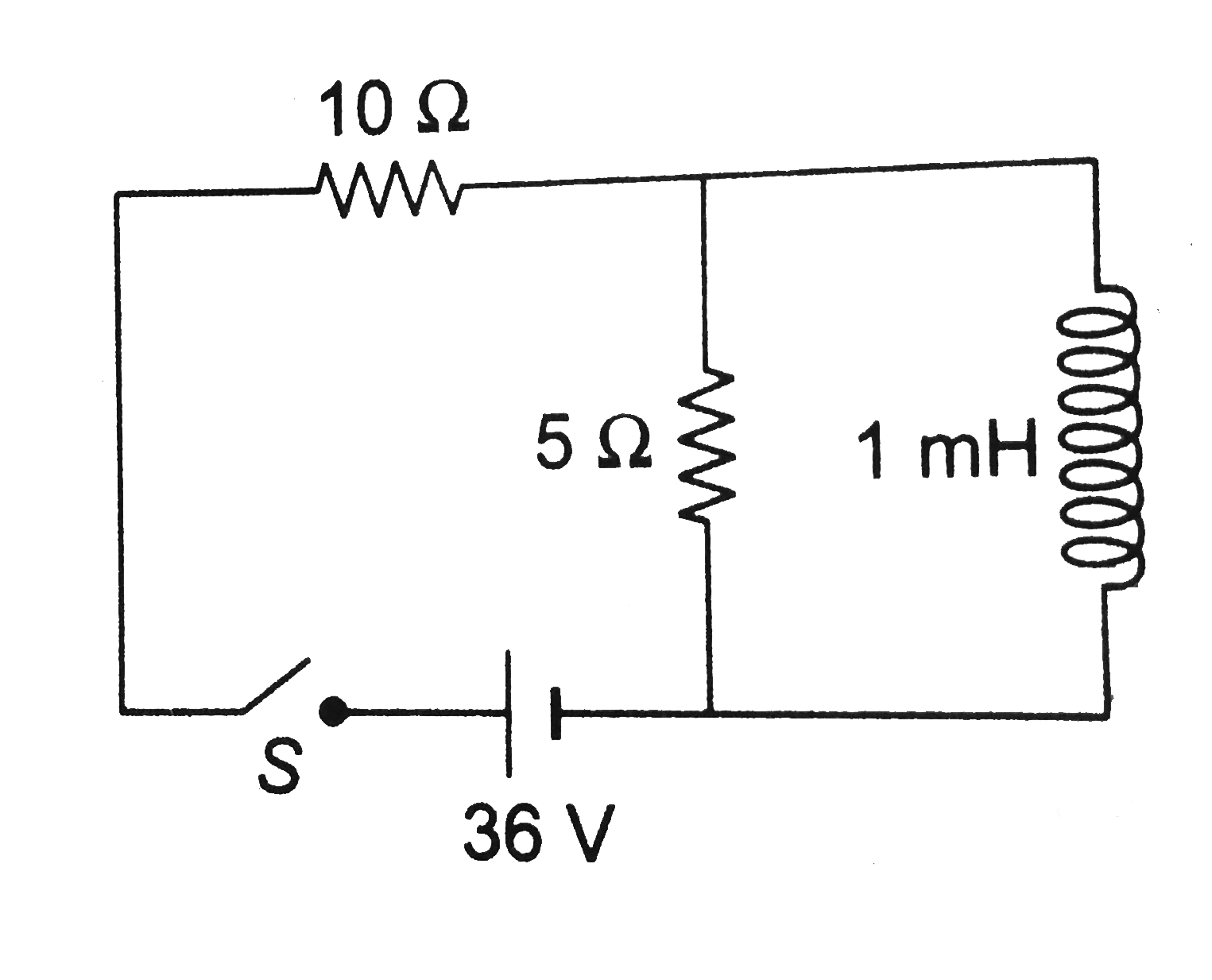
View SolutionFigure-5.102 shows a RL circuit. If at t-0 switch is closed, find the current in inductor as a function of time.
View Solution
