A body moves between two points A and B which are at a distance a and b from the point O in the same straight line OAB. Then the amplitude of oscillation is
a+b2
√a2+b22
b−a2
b-a
The correct Answer is:C
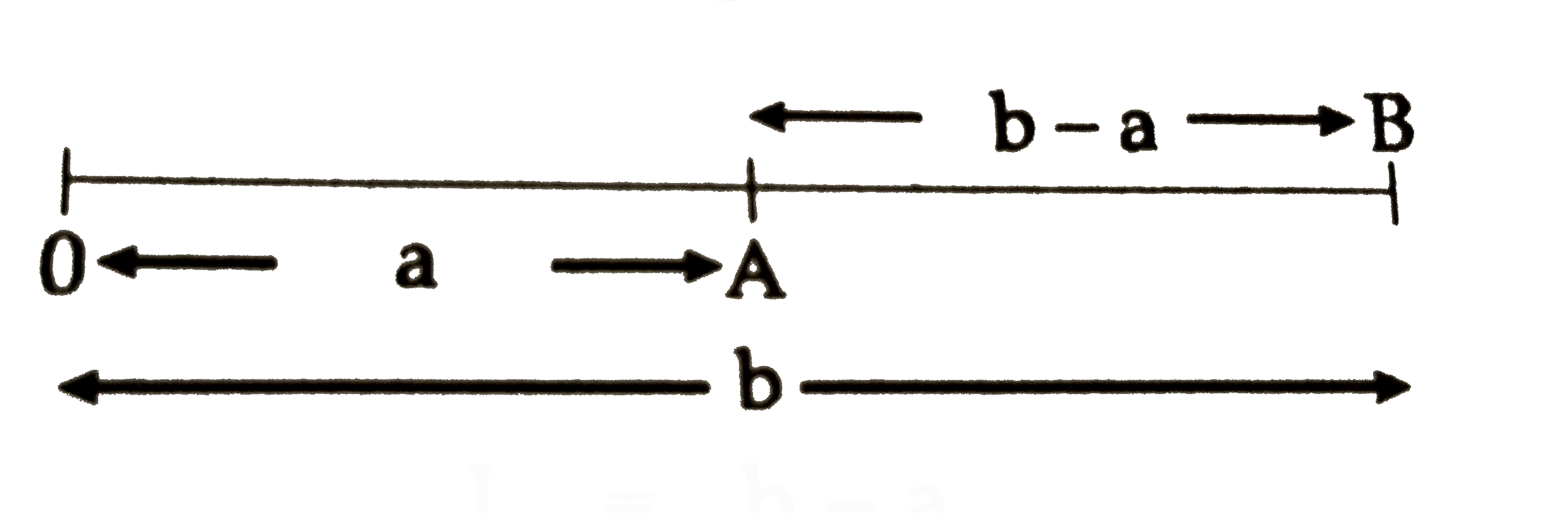
L=b−a
2A=b−a
∴A=b−a2.
Topper's Solved these Questions
Similar Questions
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line with it are 30o and 60o , then the height of the tower is √a+b (b) √ab (c) √a−b (d) √ab
View SolutionIf the angles of elevation of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is ab (b) √ab (c) ab (d) √ab
View Solution
Knowledge Check
The angles of elevation of the top of a tower at two points, which are at distances a and b from the foot in the same horizontal line and on the same side of the tower, are complementary. The height of the tower is
AabB√abC√a/bD√b/aIf the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
A√abB√abC√a+bD√a−bThe angle of elevation of the top of a tower from the point P and Q at distance of a and b respectively from the base of the tower and in the same straight line with it are complementary .The height of the tower is
A√abBabCabDa2b2
The angle of elevation of the top of a tower from two points on the ground at distances a metres and b metres from the base of the tower and in the same straight line are complementary.Prove that height of the tower is√ab.
View SolutionThe angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionIf the angle of elevation of a tower from two distant points a and b (a > b) from its foot and in the same straight line and on the same side of it are 30∘and60∘, then the height of the tower is
View SolutionThe distance between two consecutive points which are in the same state of oscillation is
View SolutionA particle performs SHM in a straight line. In the first second, starting from rest, it travels a distance a and in the next second it travels a distance b in the same direction. The amplitude of the SHM is
View Solution

