If the angle of elevation of a tower from two distant points a and b (a > b) from its foot and in the same straight line and on the same side of it are 30∘and60∘, then the height of the tower is
a )√ab
b)√a+b
c) √ab
d ) √a−b
The correct Answer is:C
To find the height of the tower given the angles of elevation from two points A and B, we can follow these steps:
Step 1: Understand the problem
We have a tower and two points A and B on the ground from which the angles of elevation to the top of the tower are given as 30° and 60°, respectively. Point A is farther away from the tower than point B.
Step 2: Set up the diagram
Let:
- h = height of the tower
- a = distance from point A to the foot of the tower
- b = distance from point B to the foot of the tower
Step 3: Use trigonometric ratios
From point A (angle of elevation = 30°):
tan(30°)=ha
We know that tan(30°)=1√3, so:
1√3=ha⟹h=a√3(Equation 1)
From point B (angle of elevation = 60°):
tan(60°)=hb
We know that tan(60°)=√3, so:
√3=hb⟹h=b√3(Equation 2)
Step 4: Equate the two expressions for height
From Equation 1 and Equation 2, we have:
a√3=b√3
Step 5: Solve for a in terms of b
Multiplying both sides by √3:
a=3b
Step 6: Substitute back to find height
Now substitute a=3b into either Equation 1 or Equation 2. We will use Equation 2:
h=b√3
Substituting a:
h=3b√3=b√3
Step 7: Final expression for height
We can express h in terms of a or b. Using b=a3:
h=a3√3
Conclusion
The height of the tower h can be expressed as:
h=√ab
We have a tower and two points A and B on the ground from which the angles of elevation to the top of the tower are given as 30° and 60°, respectively. Point A is farther away from the tower than point B.
Let:
- h = height of the tower
- a = distance from point A to the foot of the tower
- b = distance from point B to the foot of the tower
From point A (angle of elevation = 30°):
tan(30°)=ha
We know that tan(30°)=1√3, so:
1√3=ha⟹h=a√3(Equation 1)
tan(60°)=hb
We know that tan(60°)=√3, so:
√3=hb⟹h=b√3(Equation 2)
From Equation 1 and Equation 2, we have:
a√3=b√3
Multiplying both sides by √3:
a=3b
Now substitute a=3b into either Equation 1 or Equation 2. We will use Equation 2:
h=b√3
Substituting a:
h=3b√3=b√3
We can express h in terms of a or b. Using b=a3:
h=a3√3
The height of the tower h can be expressed as:
h=√ab
Topper's Solved these Questions
- HEIGHT AND DISTANCEBook:ARIHANT SSCChapter:HEIGHT AND DISTANCEExercise:Multi Concept QUESTIONS
Explore 2 Videos
- HCF AND LCMBook:ARIHANT SSCChapter:HCF AND LCMExercise:Exercise Higher Skill Level Questions
Explore 18 Videos
- INDICES AND SURDSBook:ARIHANT SSCChapter:INDICES AND SURDSExercise:HIGHER SKILL LEVEL QUESTIONS
Explore 17 Videos
Similar Questions
If the angles of elevation of a tower from two points distant a and b (a>b) from its foot and in the same straight line with it are 30o and 60o , then the height of the tower is √a+b (b) √ab (c) √a−b (d) √ab
View Solution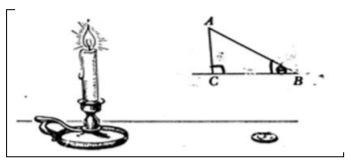
If the angles of elevation of the top of the candle from two coins distant ‘a’ cm and ‘b’ cm (a>b) from its base and in the same straight line from it are 30∘ and 60∘, then find the height of the candle.
View Solution
Knowledge Check
If the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
A√abB√abC√a+bD√a−bThe angle of elevation of a tower from a distance 100 m from its foot is 30∘ .Height of the tower is :
A100√3mB50√3mC200√3 mD100√3mThe angles of elevation of the top of a tower at two points, which are at distances a and b from the foot in the same horizontal line and on the same side of the tower, are complementary. The height of the tower is
AabB√abC√a/bD√b/a
If the angles of elevation of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is ab (b) √ab (c) ab (d) √ab
View SolutionThe angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60∘and30∘ respectively . Find the height of the tower .
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View SolutionThe angle of elevation of a tower from a distance 200 m from its foot is 30∘, Height of the tower is
View Solution
