If the orbital velocity of a planet is given by v=GaMbRc then
a=12,b=12,c=−12
a=12,b=−12,c=12
a=12,b=−12,c=−12
a=13,b=13,c=−13
The correct Answer is:A
The orbital velocity of a planet is given by
v=√GMR=G1/2M1/2R−1/2
Comparing this with v=GaMbRc we get
a=12,b=12 and c=−12
Topper's Solved these Questions
- GRAVITATION BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -2
20 Videos
- ELECTROSTATICSBOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP
20 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
Similar Questions
If orbital velocity of a planet is given by v=GaMbRc, then what is the value of 2a+b−3c3b? [Where G= gravitational constant, M = mass of planet, R = Radius of orbit]
View SolutionThe orbital velocity v of a satellite may depend on its mass m , the distane r from the centre of the earth and acceleration due to gravity g . Obtain an expression for its orbital velocity .
View Solution
Knowledge Check
If orbit velocity of planet is given by v=GaMbRc, then
Aa=13,b=13,c=−13Ba=13,b=12,c=−12Ca=12,b=−12,c=12Da=12,b=−12,c=−12The orbital velocity of the planet will be minimum at :
 AABBCCDD
AABBCCDDThe orbital velocity of the planet will be minimum at :
 AABBCCDD
AABBCCDD
A planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionThe velocity fo a body is expressed as V=GaMbRc where G is gravitational constant. M is mass, R is radius. The values of exponents a,b and c are:
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it i at the farthest distanec from the sun is
View SolutionThe orbital velocity of a planet revolving close to earth's surface is
View SolutionThe orbital velocity of a satellite at point B with radius rB and n. The radius of a point A is rA. If the orbit is increased in radial distance so that rA becomes .12rA find the orbital velocity at (1.2rA):
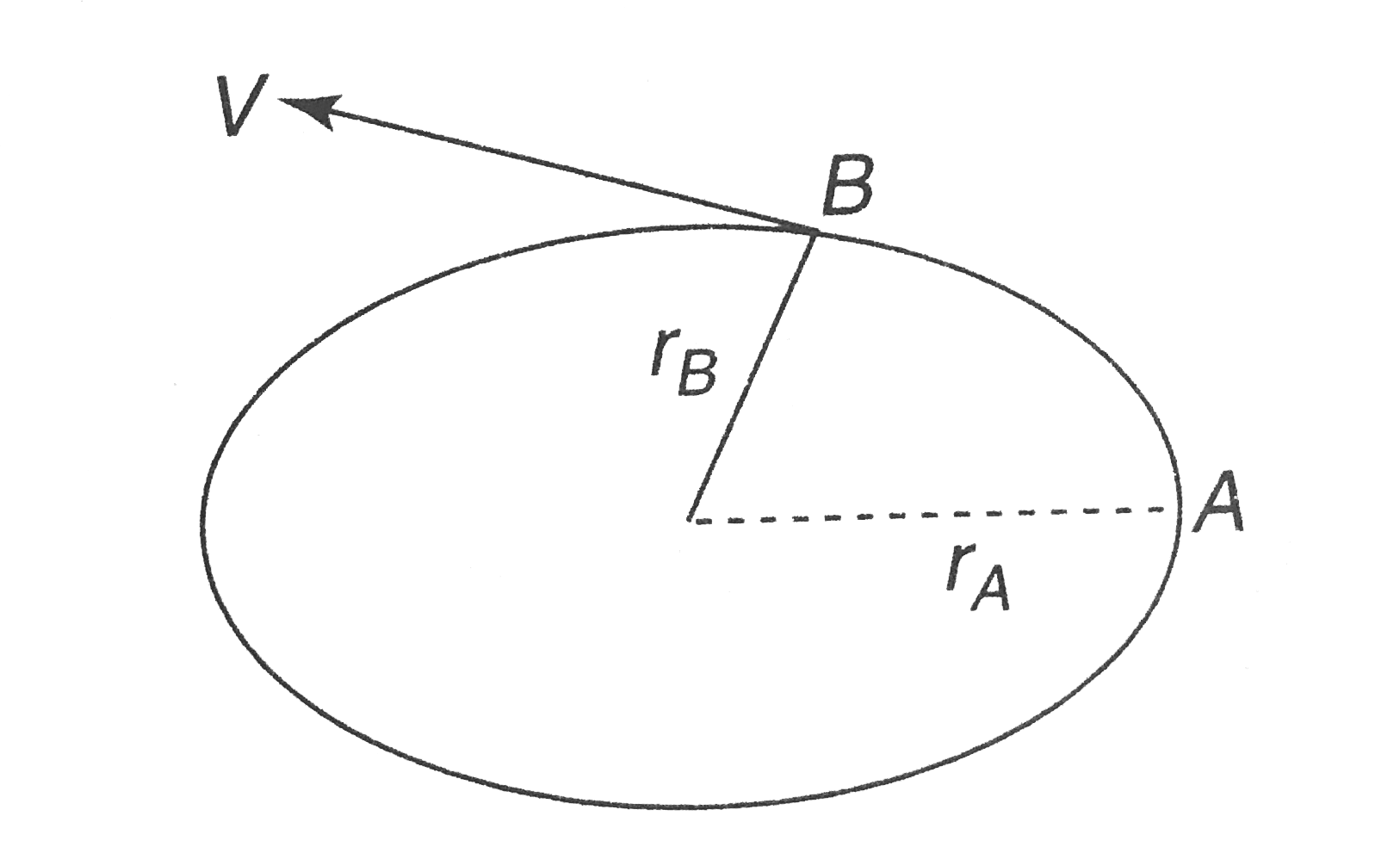
View Solution
