A thin non conducting disc of radius R is rotating clockwise (see figu

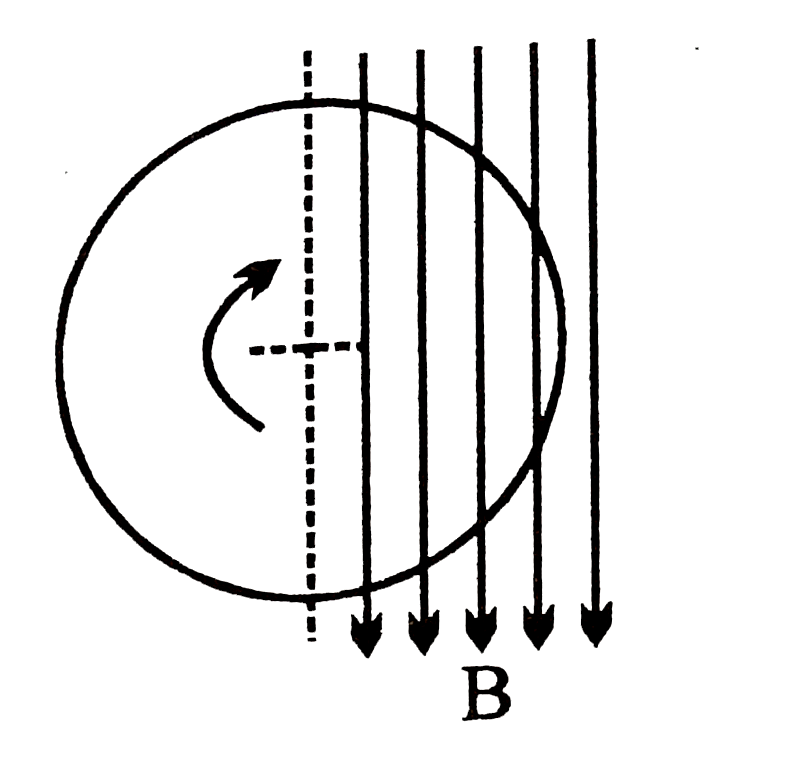A non conducting disc of radius $R$ , charge $q$ is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity $ω$ charge $q$ is uniformly distributed over its surface. The magnetic moment of the disc is
A $\frac{1}{4} q ω R^{2}$
B $\frac{1}{2} q ω R$
C $q ω R$
D $\frac{1}{2} q ω R^{2}$
A non-conducting disk of radius $R$ is rotating about its own axis with constant angular velocity $ω$ in a perpendicular uniform magnetic field $B$ as shown in figure. The emf induced between centre and rim of disk is

A $\frac{B ω R^{2}}{2}$
B $B ω R^{2}$
CZero
D $\frac{B ω R^{2}}{3}$
A nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity $ω$ . The magnt moment of this disc is .
A $\frac{1}{4} q ω R^{2}$
B $\frac{1}{2} q ω R$
C $q ω R$
D $\frac{1}{2} q ω R^{2}$

The correct Answer is:A