A variable frequency 230 V alternating voltage source is connected across a series combination of and
(i) Calculate the angular frequency fo the source which drives the circuit in resonance.
(ii) Obtain r.m.s. the impedance of the circuit and amplitude of current at resonance frequency
(iii) Obtain r.m.s. potential drop across the three elements of the circuit at resonating frequency.
(iv) How do you explain the observation that the algerbraic sum of voltages across the three elements obtained is greater than the supplied voltage.
To solve the given problem step by step, we will address each part of the question sequentially.
Given Data:
- Inductance, L=5.0H
- Capacitance, C=80μF=80×10−6F
- Resistance, R=40Ω
- Voltage, V=230V
(i) Calculate the angular frequency of the source which drives the circuit in resonance.
At resonance in an RLC circuit, the inductive reactance XL equals the capacitive reactance XC. The formula for angular frequency ω at resonance is given by:
ω=1√LC
Substituting the values:
ω=1√5.0×80×10−6
Calculating LC:
LC=5.0×80×10−6=4.0×10−4
Now, calculating √LC:
√LC=√4.0×10−4=0.02
Thus,
ω=10.02=50rad/s
(ii) Obtain r.m.s. impedance of the circuit and amplitude of current at resonance frequency.
At resonance, the impedance Z is equal to the resistance R:
Z=R=40Ω
The r.m.s. current Irms can be calculated using Ohm's law:
Irms=VrmsZ
Substituting the values:
Irms=23040=5.75A
(iii) Obtain r.m.s. potential drop across the three elements of the circuit at resonating frequency.
1. Voltage across the resistor VR:
VR=Irms×R=5.75×40=230V
2. Voltage across the inductor VL:
VL=Irms×XL=Irms×ωL
Where XL=ωL=50×5=250Ω
VL=5.75×250=1437.5V
3. Voltage across the capacitor VC:
VC=Irms×XC=Irms×1ωC
Where XC=1ωC=150×80×10−6=250Ω
VC=5.75×250=1437.5V
(iv) Explanation of the observation that the algebraic sum of voltages across the three elements is greater than the supplied voltage.
The voltages across the inductor and capacitor are out of phase by 180 degrees. Therefore, they can be represented as:
VL+VC=1437.5−1437.5=0
The total voltage across the circuit is:
Vtotal=VR+(VL−VC)=230+0=230V
The algebraic sum of the voltages across the inductor and capacitor does not contribute to the total voltage because they cancel each other out. Thus, the observed phenomenon is due to the phase difference between the voltages across the inductor and capacitor.
- Inductance, L=5.0H
- Capacitance, C=80μF=80×10−6F
- Resistance, R=40Ω
- Voltage, V=230V
VR=Irms×R=5.75×40=230V
VL=Irms×XL=Irms×ωL
Where XL=ωL=50×5=250Ω
VL=5.75×250=1437.5V
VC=Irms×XC=Irms×1ωC
Where XC=1ωC=150×80×10−6=250Ω
VC=5.75×250=1437.5V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:JEE Mains Ad..(Multiple Choice Question)
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Multiple Choice Questions
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Value Based Questions
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:II Focus multiple choice question
Explore 5 Videos
Similar Questions
Fig 14.18 shows a series LCR circuit connected to a variable frequency 200 V source:
L=4.0H,C=100μF and R=40Ω.
(i) Calculate the resonant frequency of the circuit.
(ii) Obtain the impedance of the circuit and the amplitude of the current at resonating frequency.
(iii) Determine r.m.s. potential drop across L.

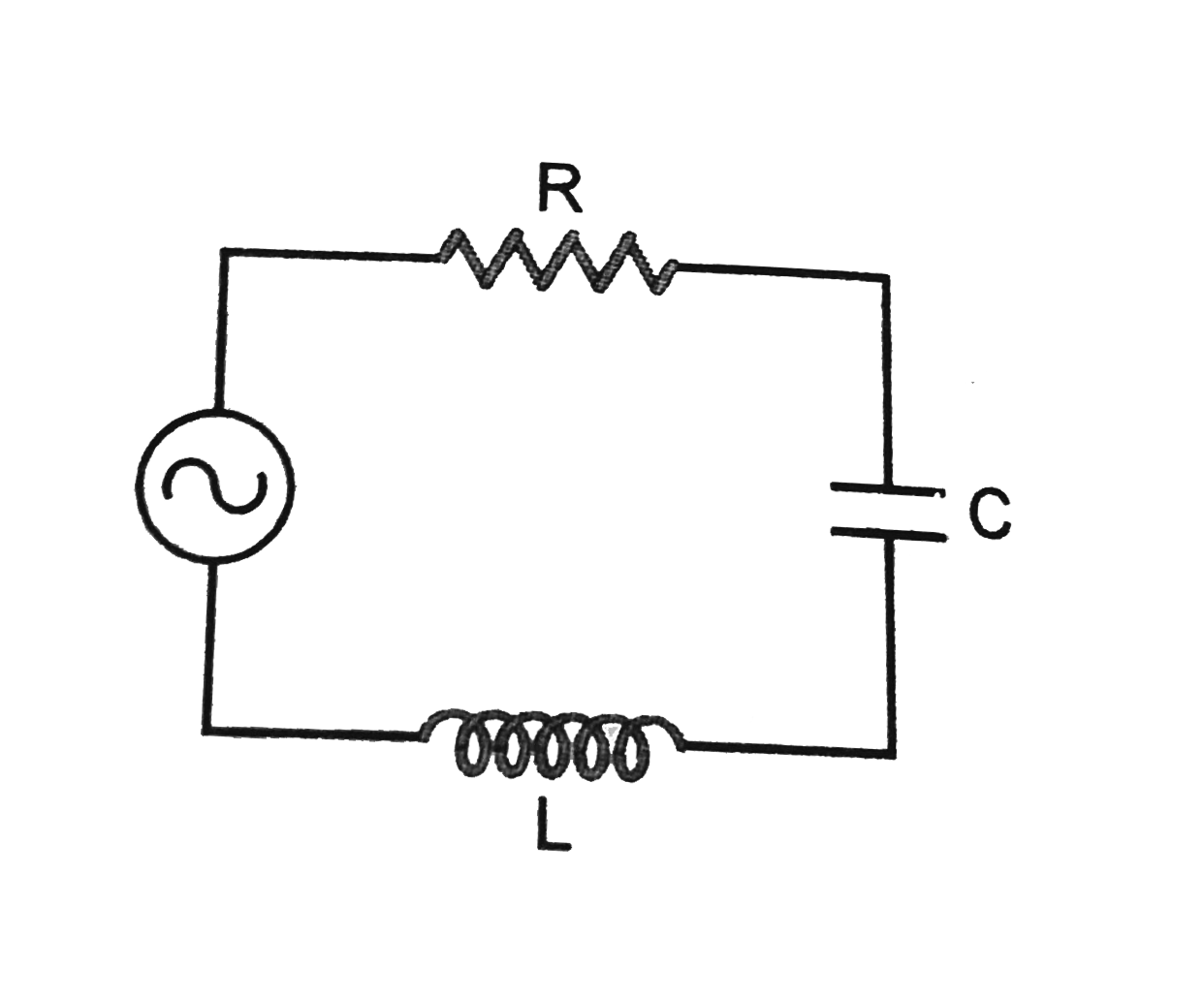
View SolutionA series LCR circuit connected to a variable frequency 230 V source has L = 5.0 H, C=80μF, R=40Ω, Fig.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and amplitude of current at at resonating frequency.
(c ) Determine the r.m.s. potential drops acorss the three elements the circuits. Show that the potential drop acorss the LC combination is zero at the resonating frequecny.
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.

View SolutionA 200 V varialbe frequency a.c. source is connected to a series combination the angular C=80μF and R=40Ω. Calculate the angular frequency of the soucre to get maximum current in the cicuit, the current amplitude at resonance and power dissipated in the circuit.
View SolutionA series LCR circuit with L=4.0h,C=100μF and R=60Ω is connected to a varialbe frequency 240 V source. Calcalate
(i) angular frequency of the source which drives the circuit in resonace,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductro at resonance.
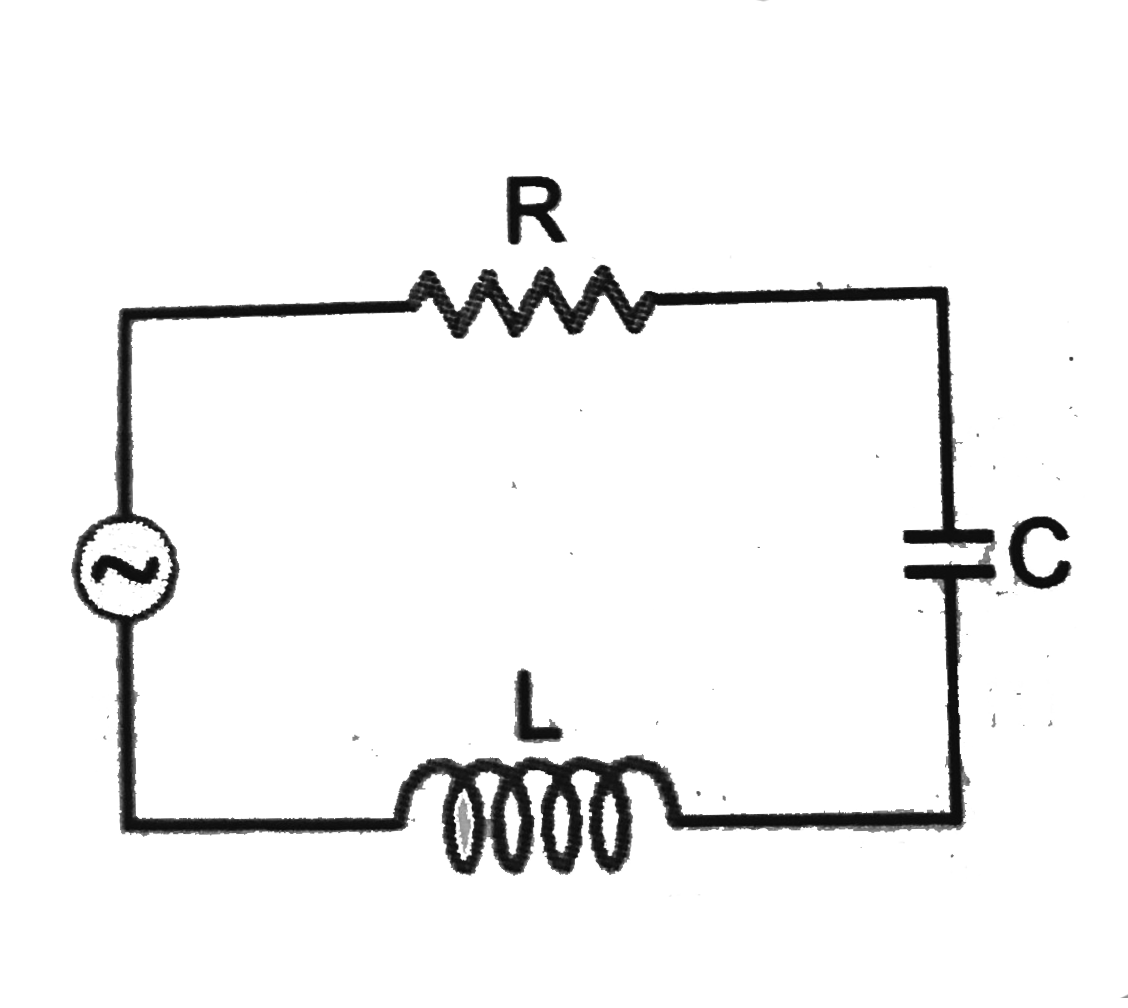
View SolutionFig. shows series LCR circuit with L=5.0H,C=80μF,R=40Ω connected to a variable frequency 240 V source. Calculate
(i) the angular freuquency of the source which drives the circuit at resonance.
(ii) Current at the resonanting frequency.
(iii) the rms pot. drop across the capacitor at resonance.
View SolutionAn AC source of rms voltage 220 V and variable frequency is connected across a series combination of 5 H inductance 80μF capacitance and 40Ω resistance . Calculate frequency which can drive the circuit to resonance. What will be the impedance of the circuit for this frequency and peak current ?
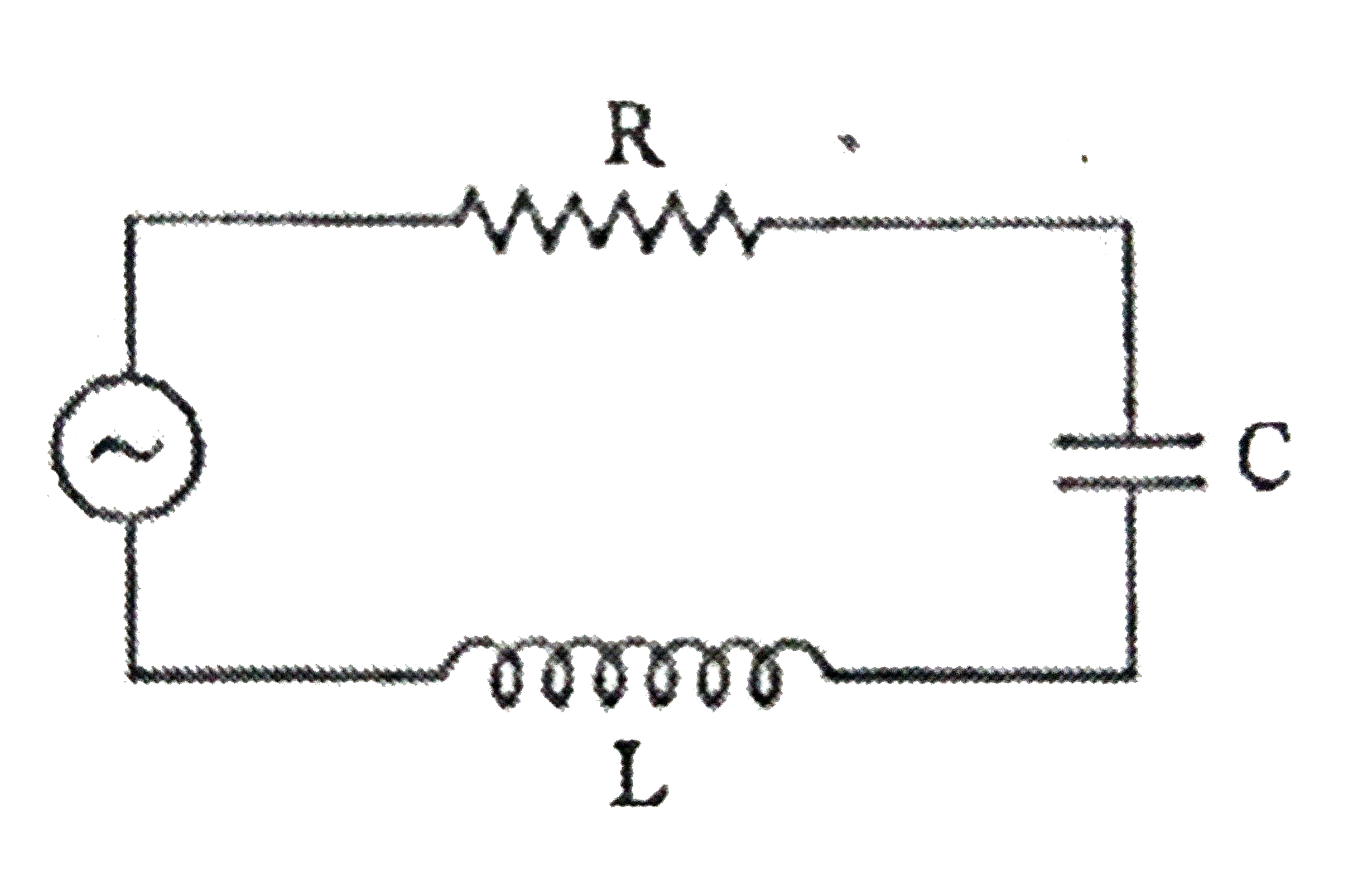
View SolutionThe figure shows a series LCR circuit with L=10.0H2,C=40μF,R=60Ω connected to a variable frequency 240 V source. Calculate
(i) The angular frequency of the source which drives the circuit at resonance.
(ii) The current at the resonating frequency.
(iii) The rms potential drop across the capacitor at resonance.
View SolutionA series LER circuit with C=80μF, L = 5.0 H and R=40Ω is connected to a variable frequency 240 V a.c. source Calculate
(i) angular frequency of the source which drives the circuit in resonanace.
(ii) current at the resonating frequency.
(iii) rms pot. drop across the capacitor.
View SolutionA series LCR circuit with L=80mH,C=50μF and R=60ohm is connected to a variable frequency 220 V source. Determine (i) the source frequency which drives the circuitin resonance (iii) the quality factor Q of the circuit.
View Solution

