The approximate formula expressing the formula of mutual inductance of two coaxial loops of the same redius $a$ when their centers are separated by a distance $l$ with $l > > a$ is

A

$\frac{1}{2} \frac{μ_{0} p a^{4}}{l^{3}}$

B

$\frac{1}{2} \frac{μ_{0} a^{4}}{l^{2}}$

C

$\frac{μ_{0}}{4 π} \frac{π a^{4}}{l^{2}}$

D

$\frac{μ_{0}}{π} \frac{a^{4}}{l^{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $I$ =current in once loop. This magnetic flux at the centre of the other co-axial loop at a distance $l$ from the centre of the first loop is
$B = \frac{μ_{0}}{4 π} \frac{2 I . π a^{2}}{{((a^{2} + l^{2}))}^{3 / 2}})$
where $p_{m} = I . π a^{2}$
=magnetic moment of loop.
the flux through the other loop is
$ϕ_{12} = B π a^{2}$
$= \frac{μ_{0}}{4 π} . \frac{2 π a^{2} I}{{(a^{2} + l^{2})}^{3 / 2}} π a^{2}$
or $\frac{ϕ_{12}}{I} = \frac{μ_{0}}{4 π} . \frac{2 π^{2} a^{4}}{2 {(a^{2 + l^{2}})}^{3 / 2}}$
$= \frac{ϕ_{0} π a^{4}}{2 {(a^{2} + l^{2})}^{3 / 2}}$
:. $μ_{12 = M_{12} I}$
:. $M_{12} = \frac{ϕ_{12}}{I} = \frac{1}{2} \frac{μ_{0} π a^{4}}{l^{3}}$
:. $a < < 1$ .

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the mutual inductance of a two-loop system as shown with centre separation l

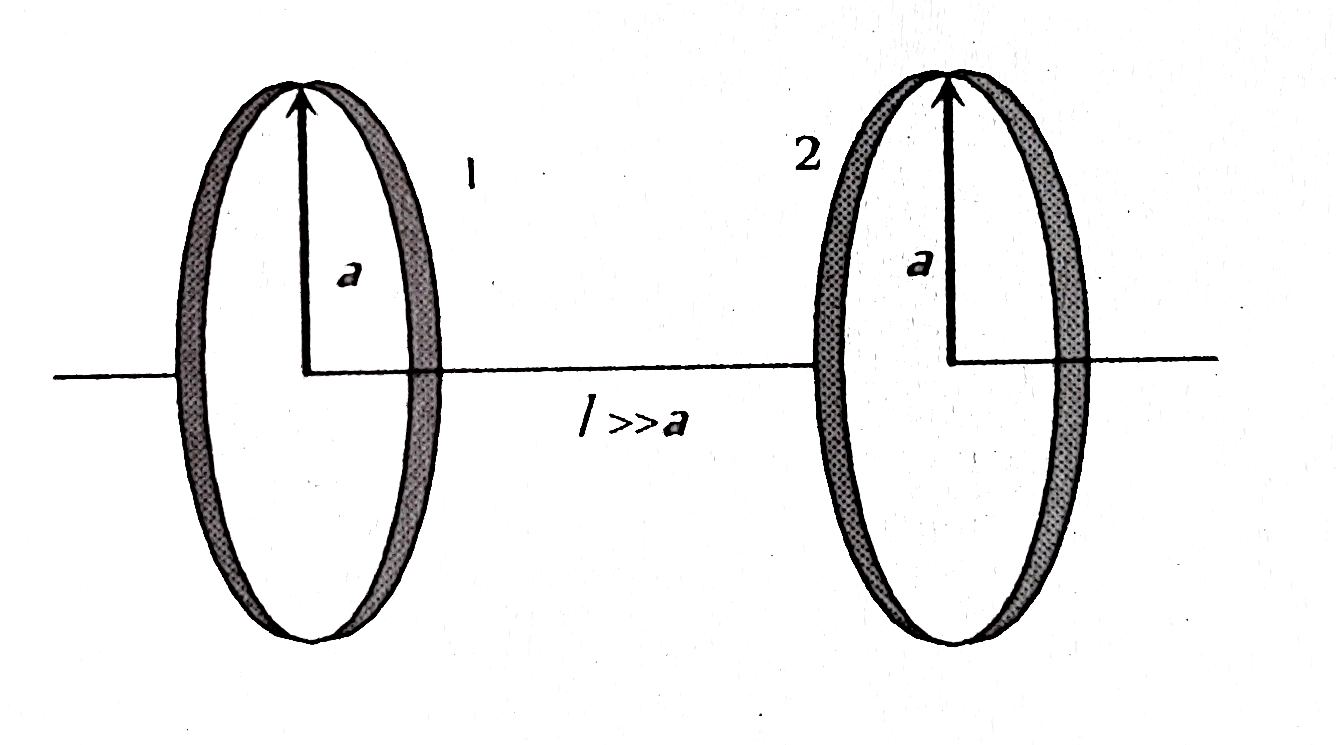A $\frac{μ_{0} π a^{4}}{8 l^{3}}$
B $\frac{μ_{0} π a^{4}}{4 l^{3}}$
C $\frac{μ_{0} π a^{4}}{6 l^{3}}$
D $\frac{μ_{0} π a^{4}}{2 l^{3}}$
Question 2 - Select One
Mutual inductance of two coils depends on their self inductance $L_{1}$ and $L_{2}$ as :
A $M_{12} = L_{1} / L_{2}$
B $M_{12} = L_{2} / L_{1}$
C $M_{12} = \sqrt{L_{1} L_{2}}$
D $M_{12} = \sqrt{L_{1} / L_{2}}$
Question 3 - Select One
What is the mutual inductance of a two-loop system as shown with centre separation $l$ ?

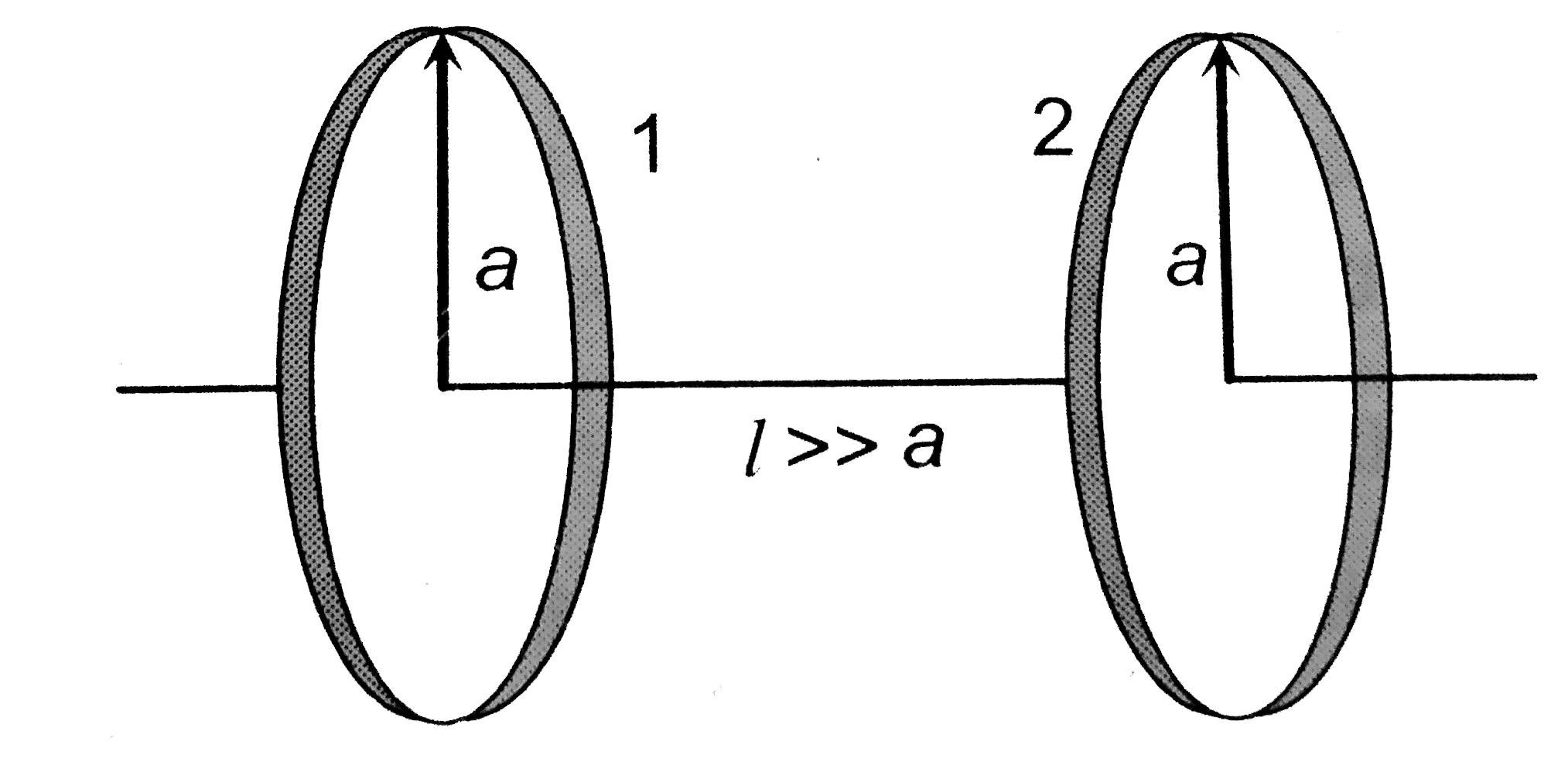A $\frac{μ_{0} π a^{4}}{8 l^{3}}$
B $\frac{μ_{0} π a^{4}}{4 l^{3}}$
C $\frac{μ_{0} π a^{4}}{6 l^{3}}$
D $\frac{μ_{0} π a^{4}}{(2 l^{3})}$

A2Z-ELECTROMAGNETIC INDUCTION-Problems On Mixed Concepts

Home
Ask Doubt
Profile