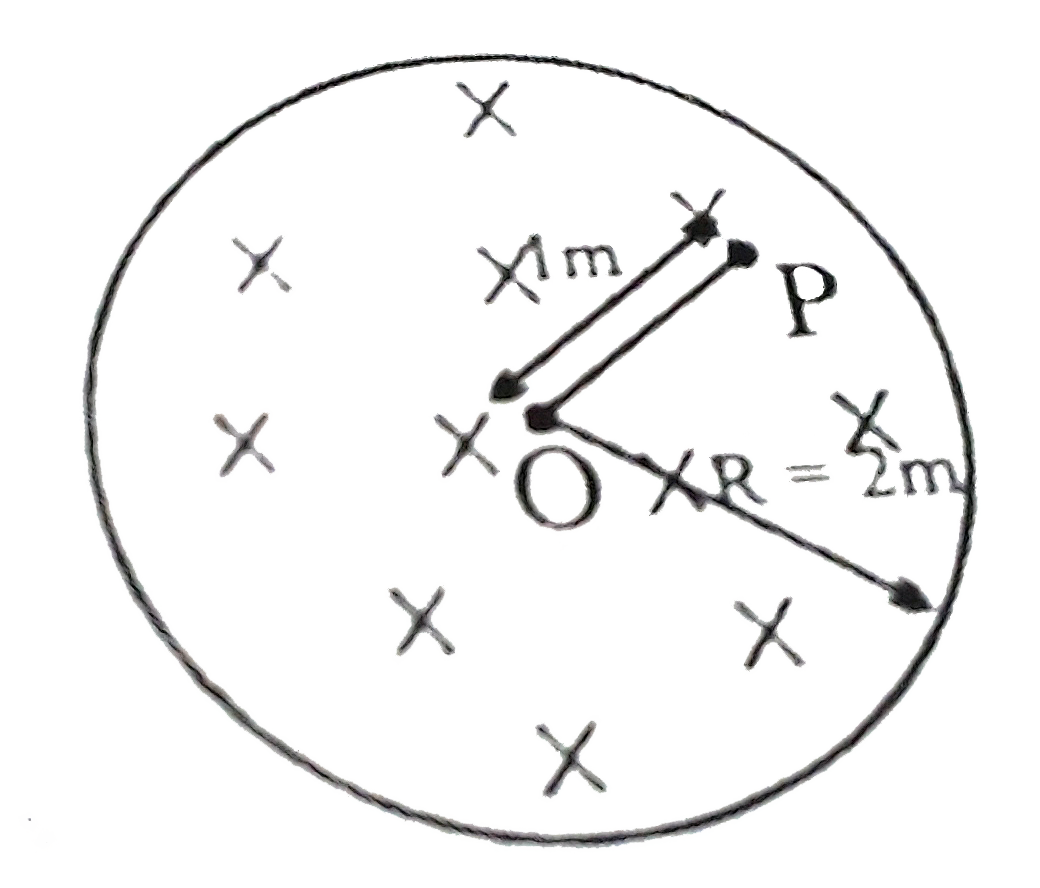
A uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

is zero
decreases as r increases
increase as r increases
none of the above
The correct Answer is:B
Constant a concentric circle of radius r. The induced electric field (E) at any point on the circle is equal to that at P. For this circle
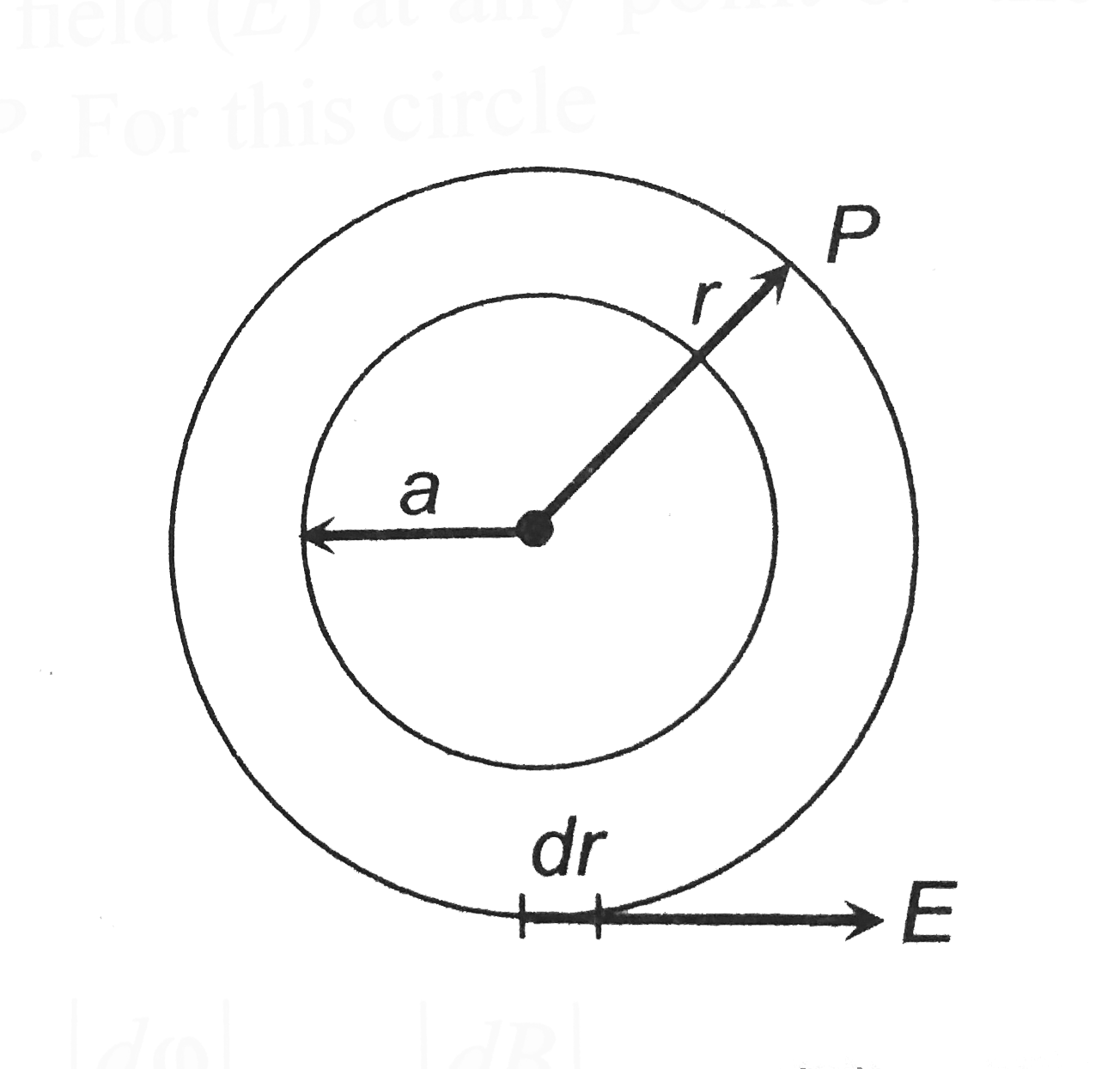
∮→E.→dl=∣∣∣dφdt∣∣∣=A∣∣∣dBdt∣∣∣
or E×(2πr)=πa2∣∣∣dBdt∣∣∣
⇒E=a22r∣∣∣dBdt∣∣∣⇒E∝1r
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section B - Assertion Reasoning
31 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - AIPMTNEET Questions
27 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Applications Of Emi
58 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
A uniform magnetic field exists in a circular region of radius R centrad at O. The field is perpendicular to the plane of paper and is strength varies with time as B=B0t. Find the induced electric field at a distance r from the centre for (i)r<R, (ii) r>R. Also, plot a graph between |E| and r for both the cases.
View SolutionA uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.

View Solution
Knowledge Check
A uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
 Ais zeroBproportional to rCproportional to 1/rDproportional 1/r2
Ais zeroBproportional to rCproportional to 1/rDproportional 1/r2A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 Ais zeroBdecreases as 1rCIncreases as rDdecreases as 1r2
Ais zeroBdecreases as 1rCIncreases as rDdecreases as 1r2A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 Ais zeroBDecreases as 1rCIncreases as rDDecreases as 1r2
Ais zeroBDecreases as 1rCIncreases as rDDecreases as 1r2
A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
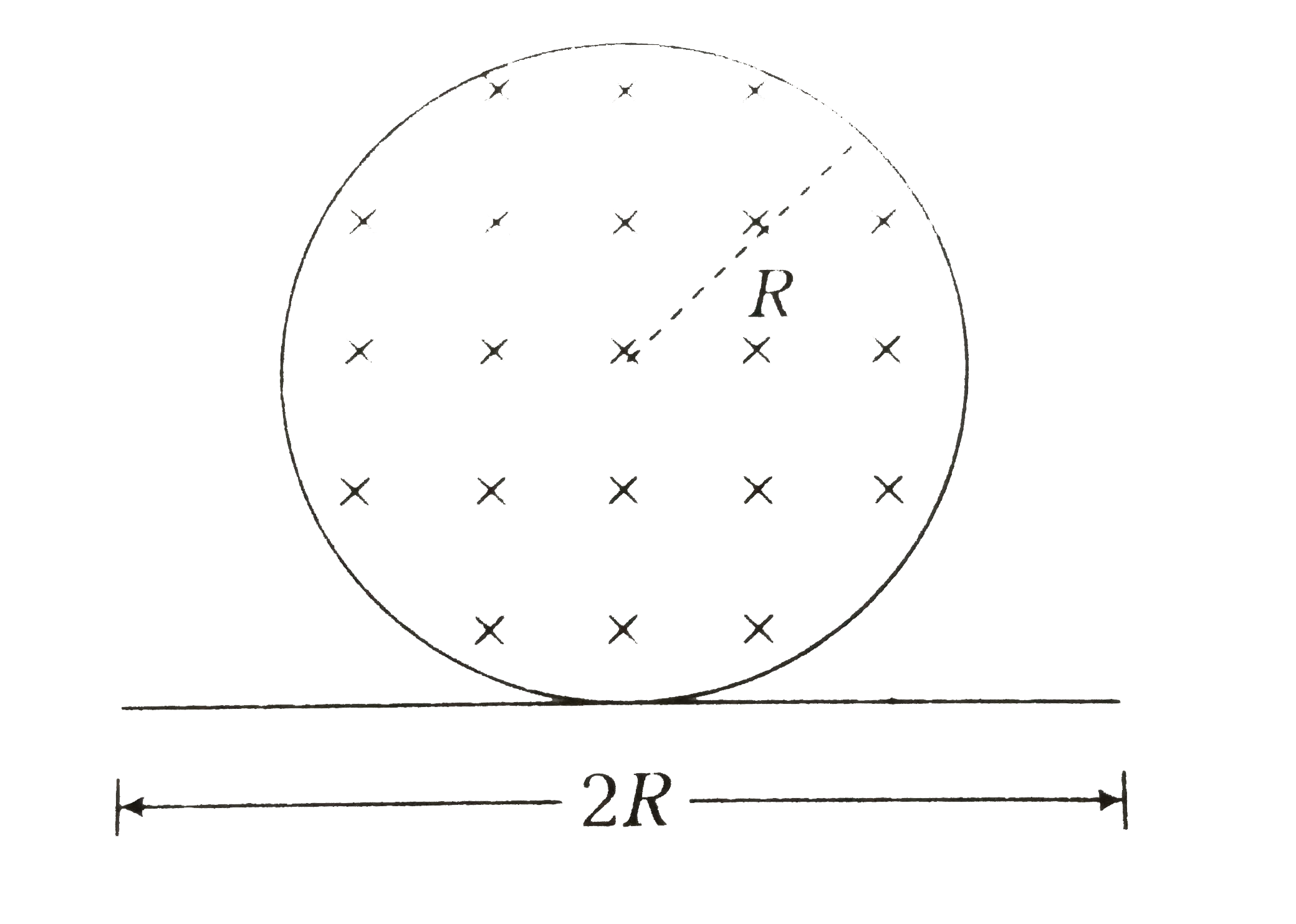
The magnitude of induced emf across the rod is
View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.

The magnitude of induced emf across the rod is
View SolutionThe magnetic field in a certain cylindrical region is changing with time according to the law B=[16−4t2] Tesla . The magnitude of induced electric field at point P at time t= time =2 sec , is
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem is
View Solution
