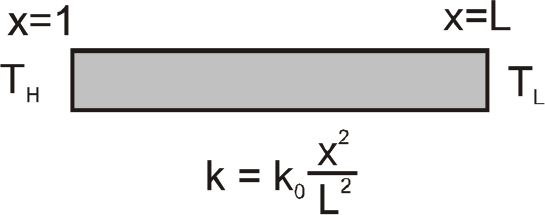
A rod of uniform cross-section but non-uniform thermal conductivity which vary as $k = k_{0} \frac{x^{2}}{L^{2}} (1 \leq x \leq L)$ (as shown in figure) is kept between fixed temperature difference for a long time. Select the correct options(s)

A

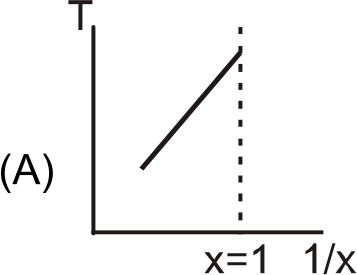
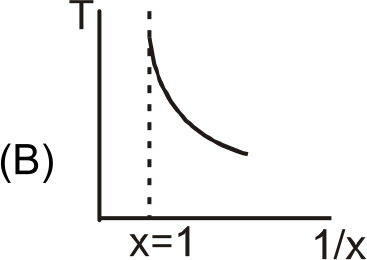
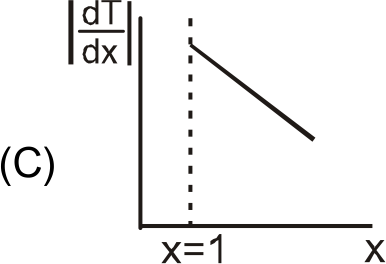
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

$i = \frac{k_{0} x^{2}}{L^{2}} A \frac{d T}{d x} \Rightarrow \int_{T_{H}}^{T} d T = - \frac{i L^{2}}{k_{0} A} \int_{1}^{x} \frac{d x}{x^{2}}$
$T - T_{H} = \frac{i L^{2}}{k_{0} A} {[\frac{1}{x}]}_{1}^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two identical rods with different thermal conductivities $k_{1} & k_{2}$ and different temperatures are first placed along length and then along area, then the ratio of rates of heat flow in both cases is
A $\frac{4 k_{1} k_{2}}{{(k_{1} + k_{2})}_{1}^{2}}$
Bnone
C $(\frac{k_{1} + k_{2}}{k_{1} - k_{2}})$
D $\frac{k_{1} k_{2}}{{(k_{1} + k_{2})}_{1}^{2}}$
Question 2 - Select One
Two bars of same length and same cross-sectional area but of different thermal conductivites $K_{1}$ and $K_{2}$ are joined end to end as shown in the figure. One end of the compound bar it is at temperature $T_{1}$ and the opposite end at temperature $T_{2}$ (where $T_{1} > T_{2}$ ). The temperature of the junction is

A $\frac{K_{1} T_{1} + K_{2} T_{2}}{K_{1} + K_{2}}$
B $\frac{K_{1} T_{2} + K_{2} T_{1}}{K_{1} + K_{2}}$
C $\frac{K_{1} (T_{1} + T_{2})}{K_{1} + K_{2}}$
D $K_{2} \frac{T_{1} + T_{2}}{K_{1}}$
Question 3 - Select One

Two ends of a rod of uniform cross sectional area are kept at temperature $3 T_{0}$ and $T_{0}$ as shown. Thermal conductivity of rod varies as $k = α T$ , (where $α$ is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
A $\sqrt{7} T_{0}$
B $\sqrt{5} T_{0}$
C $2 T_{0}$
D $\sqrt{3} T_{0}$

RESONANCE-REVISION DPP-All Questions

Home
Ask Doubt
Profile