Let the wavelength at which the the spectral emissive power of a black body (at a temperature T) is maximum, be denoted by λmax as the temperature of the body is increased by 1K, λmax decreases by 1 percent. The temperature T of the black body is
100 K
200 K
400 K
288 K
λmT=const.
lnλm=lnT=C
dλmλm+dTT=0 ∴dλmλm=dTT
Now dλmλm=−1%=−1100 (-ve sign indicates decreases)
dT=1 (given)
∴T=100K
Topper's Solved these Questions
Similar Questions
Knowledge Check
If λm denotes the wavelength at which the radiative emission from a black body at a temperature TK is maximum, then
Aλm∝T4Bλm is independent of TCλm∝TDλm∝T−1The spectral emissive power of a black body at a temperature of 6000K is maximum at λm=5000Å. If the temperature is increased by 10%, then the decrease in λm will be -
A2.5%B5.0%C7.5%D10%The maximum spectral emissive power at black body temperature 5000 K is obtained at λm=6000Å. If the temperature is increased by 10%, then decrease in λm will be
A0.15B0.1C0.05D0.03
Emissive power of an ideal black body at 127∘C is E. the temperature at which it increases to 102% is
View SolutionThe shows a radiant energy spectrum graph for a black body at at temperature T
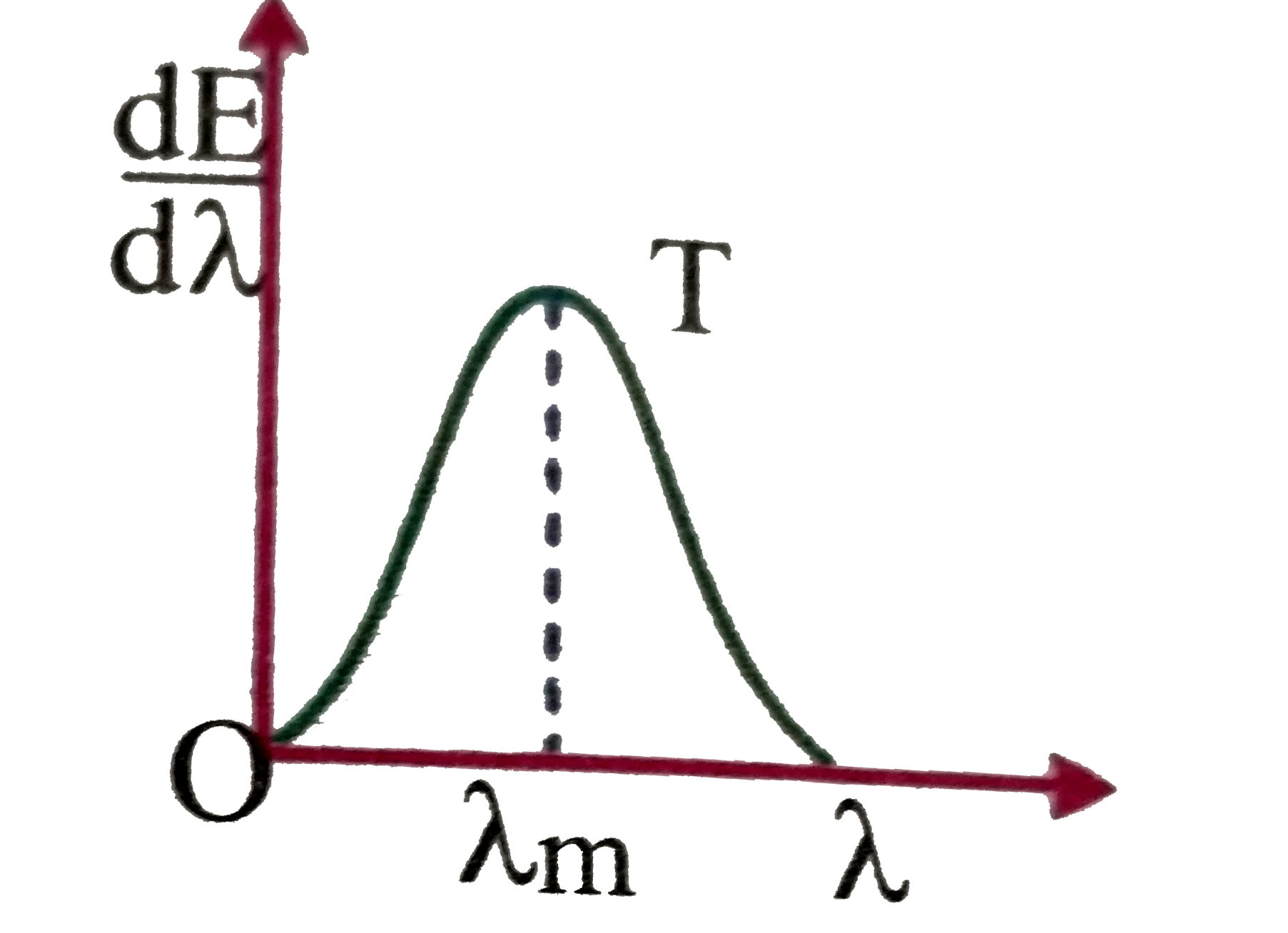
If the temperature of the body is raised to a higher temperature T then choose the correct statement (s).
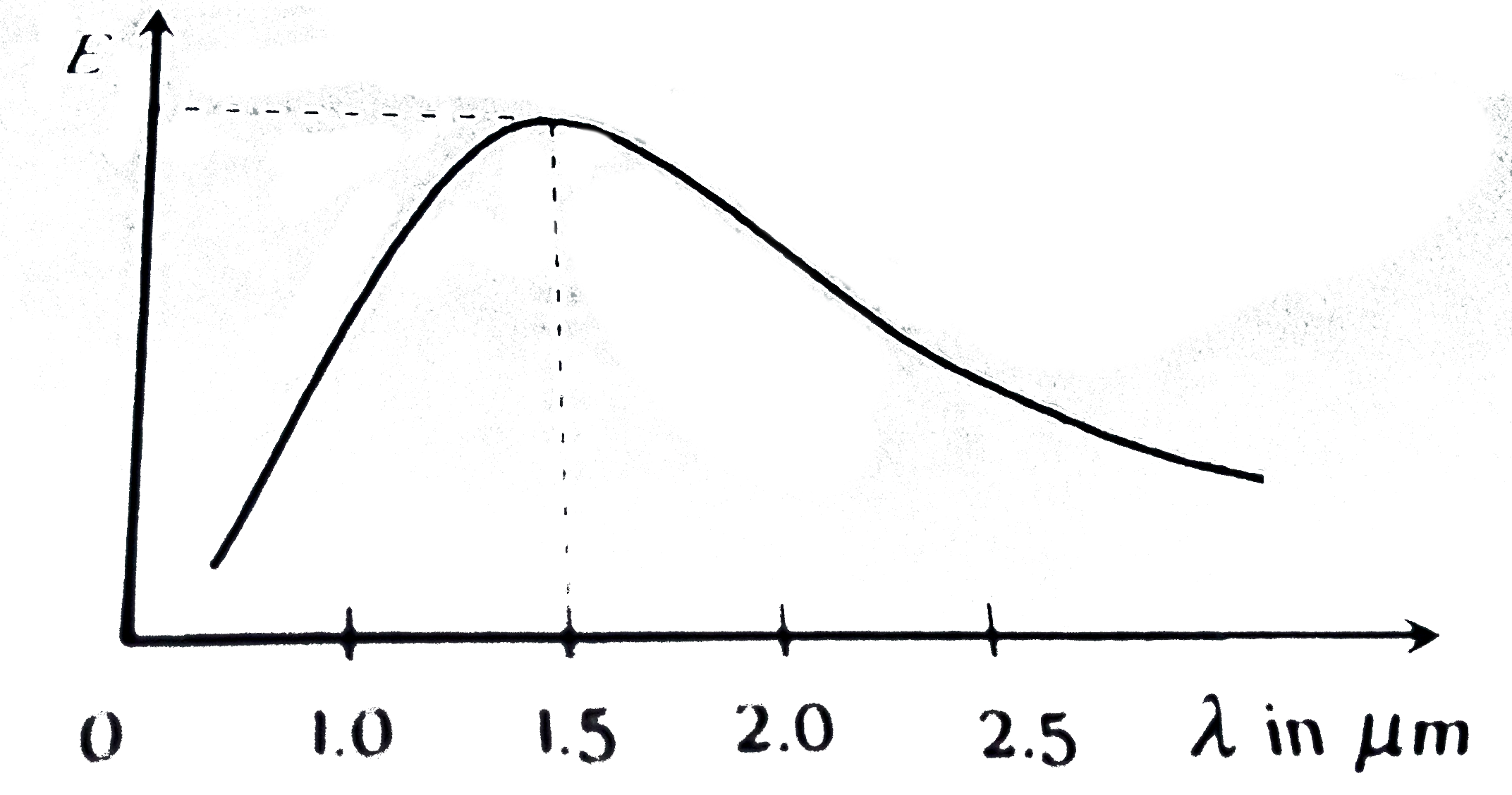
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
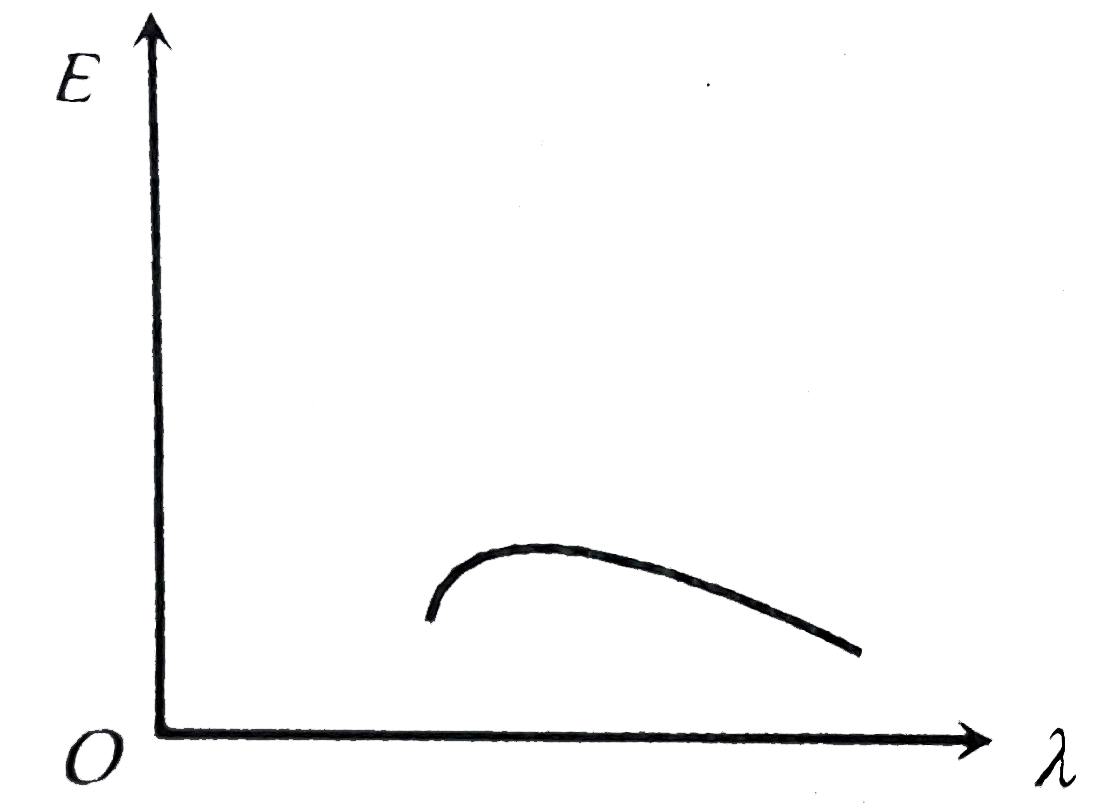
View SolutionThe energy distribution E with the wavelength (λ) for the black body radiation at temperature Kelvin T is shown in the figure. As the temperature is increased the maxima will
View SolutionThe temperature of a black body is increased by 50% , then the percentage of increases of radiation is approximetaly
View Solution

