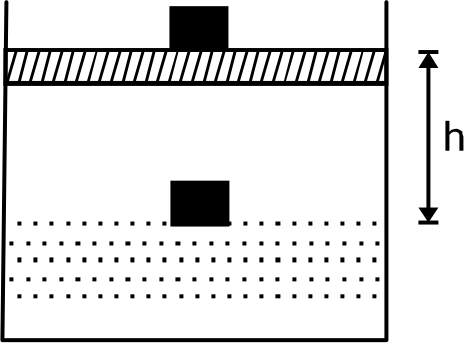
One mole of an ideal gas is contained in a perfectly insulating cylinder. Initially adiabatic piston of unit are and unit mass is in equilibrium. Now a block of same mass is kept gently on piston as shown in figure. (Take λ=1.5,g=10m/s2 and neglect friction and assume change in temperature in whole gas is simultaneous)

Maximum pressure of gas during its motion:
20√2(5−√3)3/2N/m2
20√2(3+√5)1/2N/m2
20√2(3+√5)1/2N/m2
20√2(3−√5)3/2N/m2
By energy conservation.
2mgh=42RΔT
ΔT=10hR …..(i)
Initially, mgA(A.l)=RT1 …(ii)
and finally, PmaxA(l−h)=RT2 …..(iii)
(iii)-(ii)
Pm(1−h)−10=10h …..(iv)
By equation of adiabatic process PV= constant
mgA(Al)γ=Pmax{A(l−h)}γ
10=Pm(1−h)γ
Put this Pm in equation (iv)
10(1−h)1−γ−10=10h
(1−h)1−γ−1=h
(1−h)1−γ=(h+1)
1√1−h=(1+h)⇒1(1−h)=(1+h)2
h(h2+h−1)=0
h=√5−12m
and Pn=10(1−√5−12)3/2=20√2(3−√5)3/2N/m2
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
View SolutionWhen p−n junction diode is forward biased then
View SolutionA smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P_(0) . Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
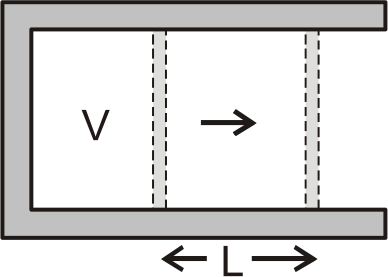
After the piston has moved by distance S. Its velocity is:
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
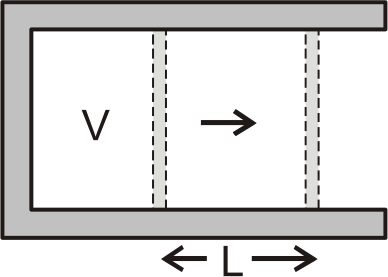
For the temperature of the gas to drop to one half of its original value. the piston will have to move by a distance:
View SolutionOne mole of an ideal gas is contained in a perfectly insulating cylinder. Initially adiabatic piston of unit are and unit mass is in equilibrium. Now a block of same mass is kept gently on piston as shown in figure. (Take λ=1.5,g=10m/s2 and neglect friction and assume change in temperature in whole gas is simultaneous)

Depth upto which (piston+block) will move before coming to rest again is :
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m ) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P_(0) and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and P_(i) be the pressure of ideal gas in initial state. Pick the correct choice:
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T_(0) The cylinder B contain identical gas at same temperature T_(0) but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V_(0) . The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T_(0) reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V_(0)/2 Then (here gamma for gas =1.5) The mass of gas in cylinder B
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas=1.5)
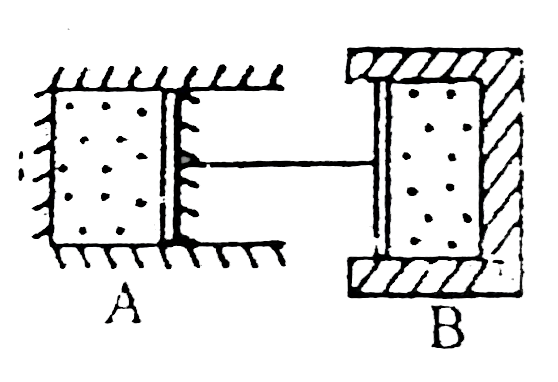
The change in internal energy of gas in cylinder A
View SolutionTwo cylinder A and B having piston conneted by massless rod (as shown in figure). The cross-sectional area two cylinders are same & equal to 'S'.The cylinder A contains m gm of an ideal gas at Pressure P & temperature T0 The cylinder B contain identical gas at same temperature T0 but has different mass. The piston is held at the state in the position so that volume of gas in cylinder A & cylinder B are same and is equal to V0. The walls & piston of cylinder A are thermally insulated, whereas cylinder B is maintained at temperature T0 reservoir. The whole system is in vacuum. Now the piston is slowly released and it moves towards left & machanical equilibrium is reached at the state when the volume of gas in cylinder A becomes V02 Then (here gamma for gas =1.5)

If work done by gas in cylinder B is WB & work done by gas in cylinder A is WA then
View SolutionAn ideal gas is enclosed in a thermally insulated container. Container is covered by an insulating piston which is connected with spring. Small displacement is given to piston as shown in figure. Which of the following statements is correct? Neglect friction everywhere.
View SolutionA cylinder with two ends is equipped with a moving piston. The gas on one side of the piston has a mass M and the other side has a mass of 2m of the same gas. If the piston is in equilibrium state, how much volume of the cylinder will be surrounded by the greater mass of gas while the temperature is the same in the whole cylinder?
View SolutionA smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P0. Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.

View SolutionTwo identical containers A and B with frictionless pistons contains the same ideal gas at the same temperature and the same volume V. The mass of the gas In A is mA and that in B is mB. The gas in each cylinder is now allowed to expand isothermally to the same final volume 2V. The changes in the pressure in A and B are found to be ΔP and 1.5ΔP respectively then:
View SolutionAn ideal gas is enclosed in a thermally insulated container. Container is covered by an insulating piston which is connected with spring. Small displacement is given to piston as shown in figure. Which of the following statements is correct? Neglect friction everywhere.
View Solution

