Question

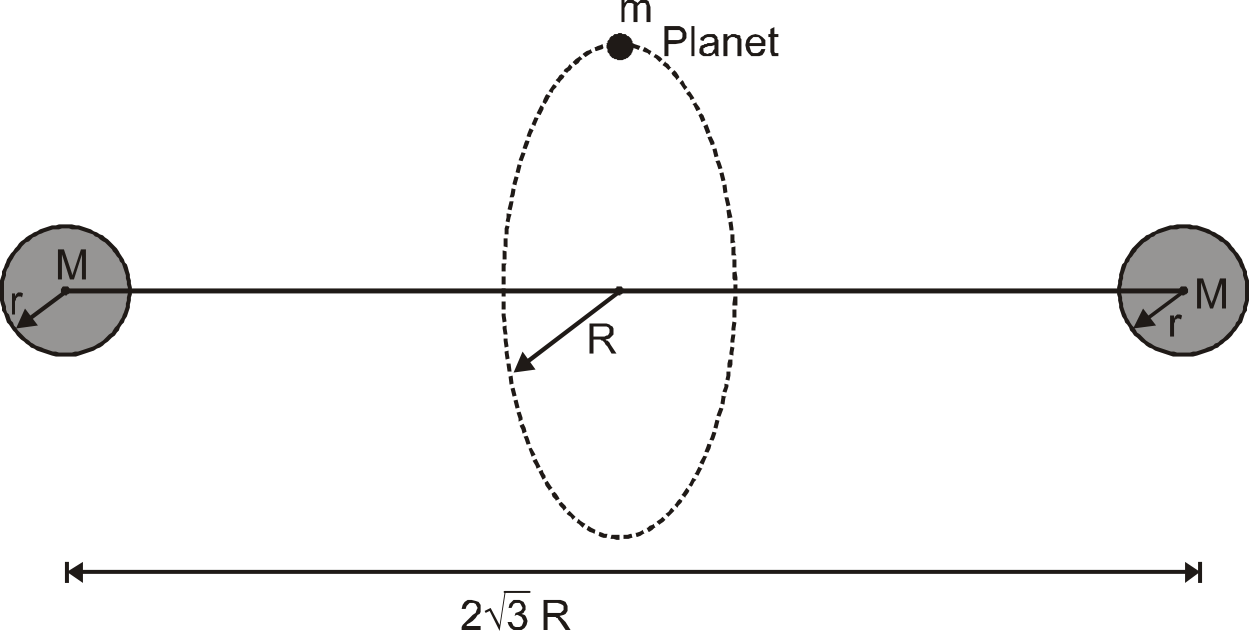
Consider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of $2\sqrt{3}R$ (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.

Options

A. `(4pi^(3//2))/(sqrt(GM))`
B. `(2piR^(3//2))/(sqrt(GM))`
C. `(piR^(3//2))/(sqrt(GM))`
D. `(3piR^(3//2))/(sqrt(GM))`

Explanation

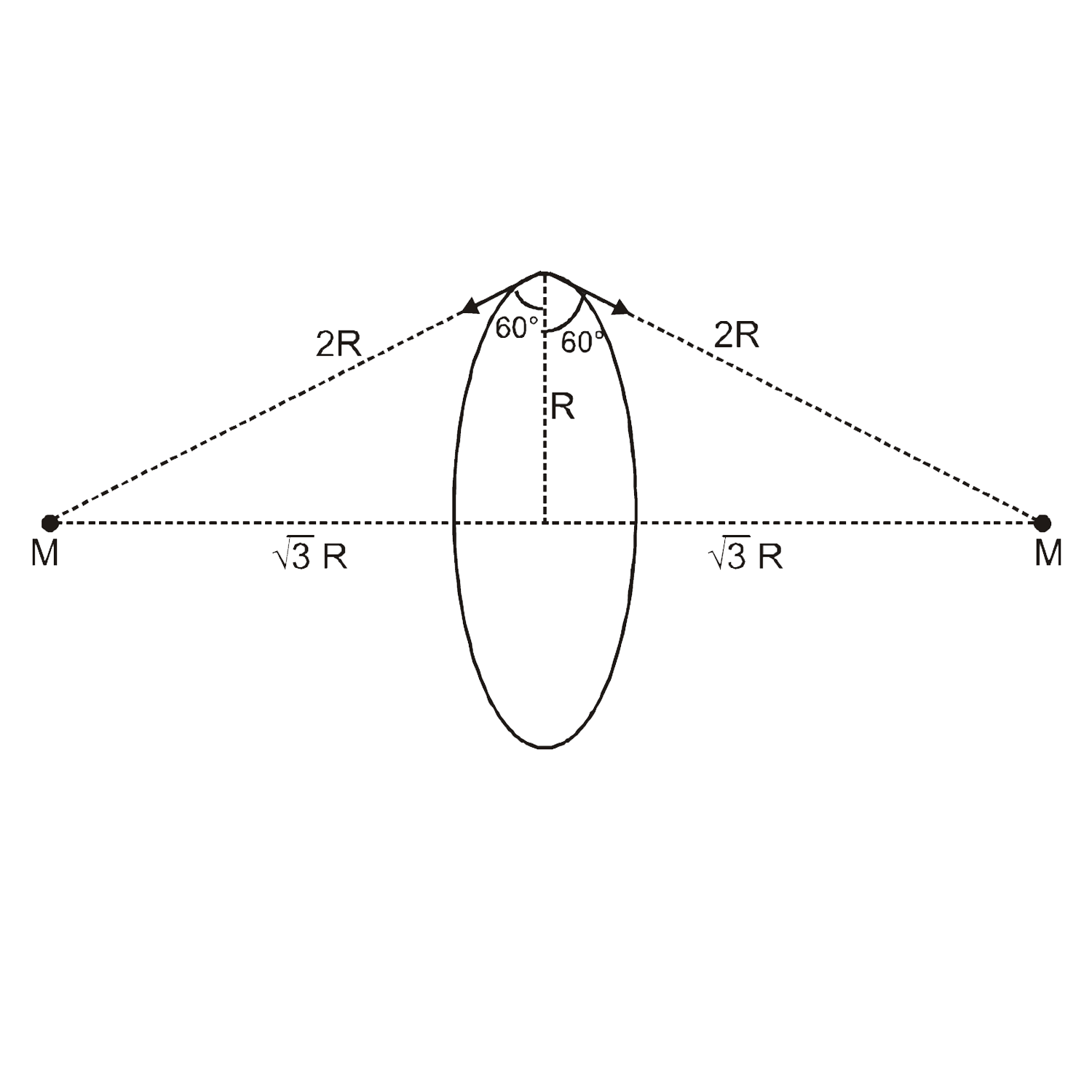
`F_("net")=2((GMm)/(4R^(2)))cos60^(@)=(GMm)/(4R^(2))`
`F_("net")=(GMm)/(4R^(2))=(mv^(2))/(R)impliesv=sqrt((GM)/(4R))=(1)/(2)sqrt((GM)/(R))`
`T=(2piR)/(v)=(4piR^(3//2))/(sqrt(GM))`
Average force on planet half revolution
`F_(avg)=(2mv)/(T//2)=(4mv)/(T)=((4mv)/(2piR))/(v)=(2mv^(2))/(piR)=(GMm)/(2piR^(2))`