Consider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of $2 \sqrt{3} R$ (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.

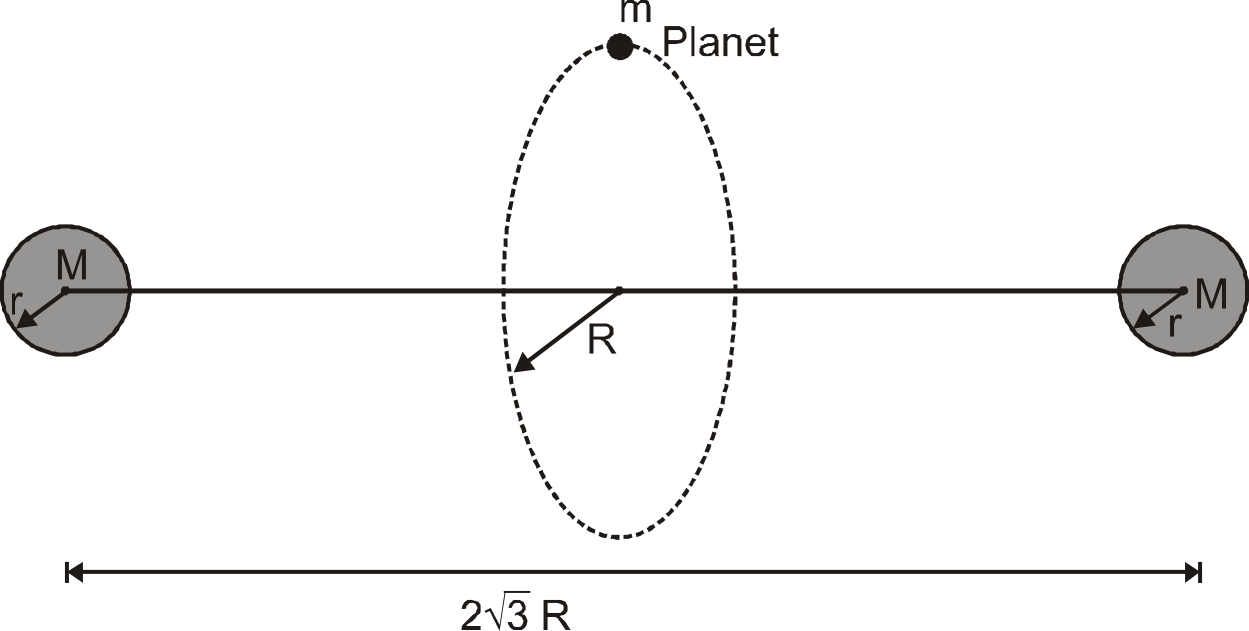
Q. Speed of the plane is

$\sqrt{\frac{G M}{8 R}}$

$\sqrt{\frac{G M}{4 R}}$

$\sqrt{\frac{G M}{2 R}}$

$\sqrt{\frac{G M}{3 R}}$

Video Solution

Text Solution

Verified by Experts

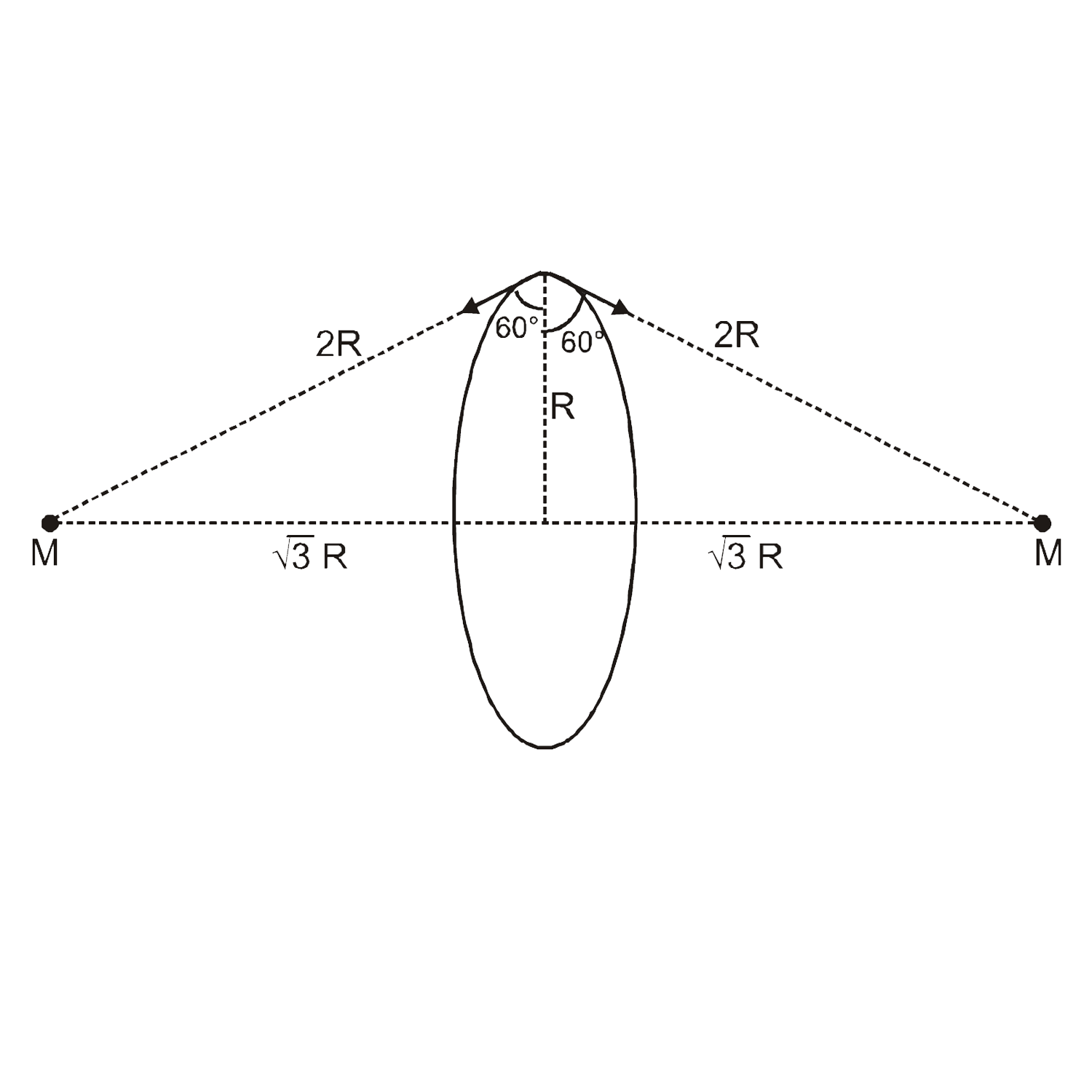
$F_{net} = 2 (\frac{G M m}{4 R^{2}}) {cos 60}^{\circ} = \frac{G M m}{4 R^{2}}$
$F_{net} = \frac{G M m}{4 R^{2}} = \frac{m v^{2}}{R} \Rightarrow v = \sqrt{\frac{G M}{4 R}} = \frac{1}{2} \sqrt{\frac{G M}{R}}$
$T = \frac{2 π R}{v} = \frac{4 π R^{3 / 2}}{\sqrt{G M}}$
Average force on planet half revolution
$F_{a v g} = \frac{2 m v}{T / 2} = \frac{4 m v}{T} = \frac{\frac{4 m v}{2 π R}}{v} = \frac{2 m v^{2}}{π R} = \frac{G M m}{2 π R^{2}}$

Updated on:21/07/2023

Consider a hypothetical solar system, which has two identical massive suns each of mass M and radius r, seperated by a seperation of $2 \sqrt{3} R$ (centre to centre). (R gtgtgtr). These suns are always at rest. There is only one planet in this solar system having mass m. This planet is revolving in circular orbit of radius R such that centre of the orbit lies at the mid point of the line joining the centres of the sun and plane of the orbit is perpendicular to the line joining the centres of the sun. Whole situation is shown in the figure.

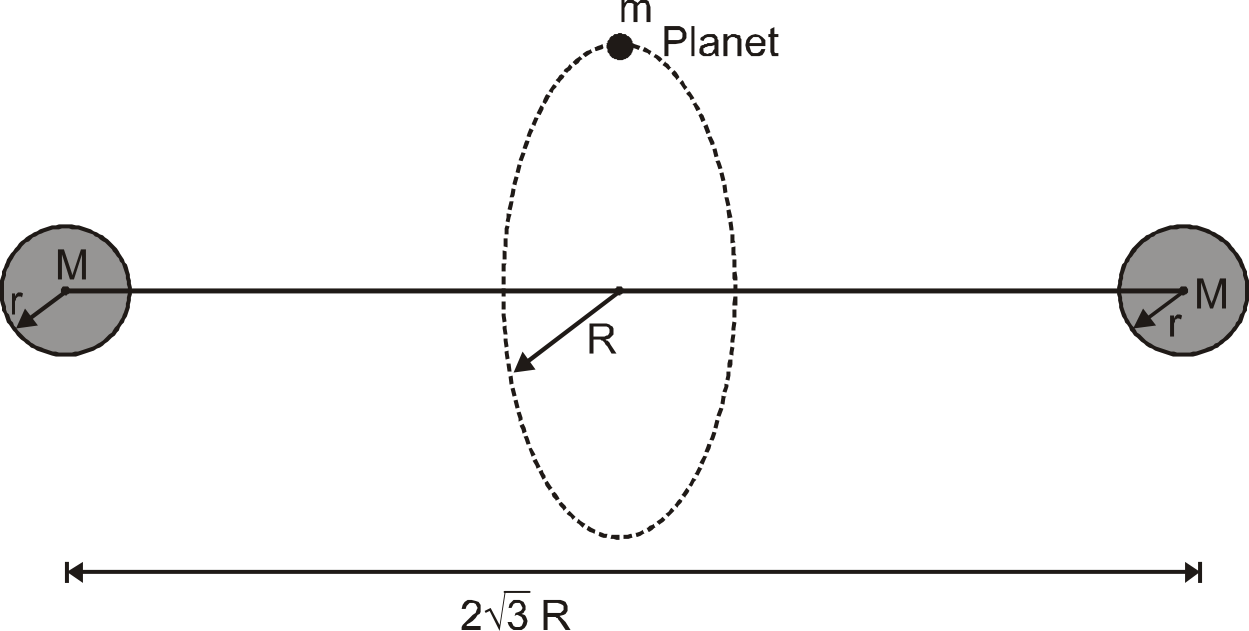
Q. Average force on the planet in half revolution is
A $\frac{G M m}{4 π R^{2}}$
B $\frac{G M m}{4 R^{2}}$
C $\frac{G M m}{2 π R^{2}}$
D $\frac{G M m}{8 R^{2}}$
If a planet of mass $m$ is revolving around the sun in a circular orbit of radius $r$ with time period, $T$ then mass of the sun is
A $4 π^{2} r^{3} / G T$
B $4 π^{2} r^{3} / G T^{2}$
C $4 π^{2} r / G T$
D $4 π^{2} r^{3} / G^{2} T^{2}$
A planet is revolving around a star in a circular orbit of radius R with a period T. If the gravitational force between the planet and the star is proportional to $R^{- 3 / 2}$ , then
A $T^{2} \propto R^{5 / 2}$
B $T^{2} \propto R^{- 7 / 2}$
C $T^{2} \propto R^{3 / 2}$
D $T^{2} \propto R^{4}$