Three particles A,B and C situated at vertices of an equilateral triangle, all moving with same constant speed such that A always move towards B,B always towards C and C always towards A. Initial seperation between each of the particle is a. O is the centroid of the triangle. Distance covered by particle A when it completes one revolution around O is
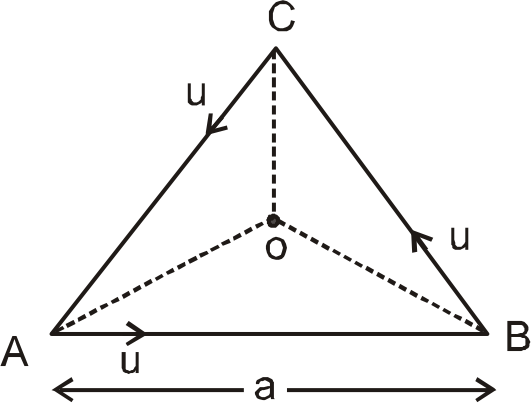
2a(1−e−2√3π)
2a3(1−e−2√3π)
a(1+e−2√3π)
2a3(1−e−√3π)
The correct Answer is:B
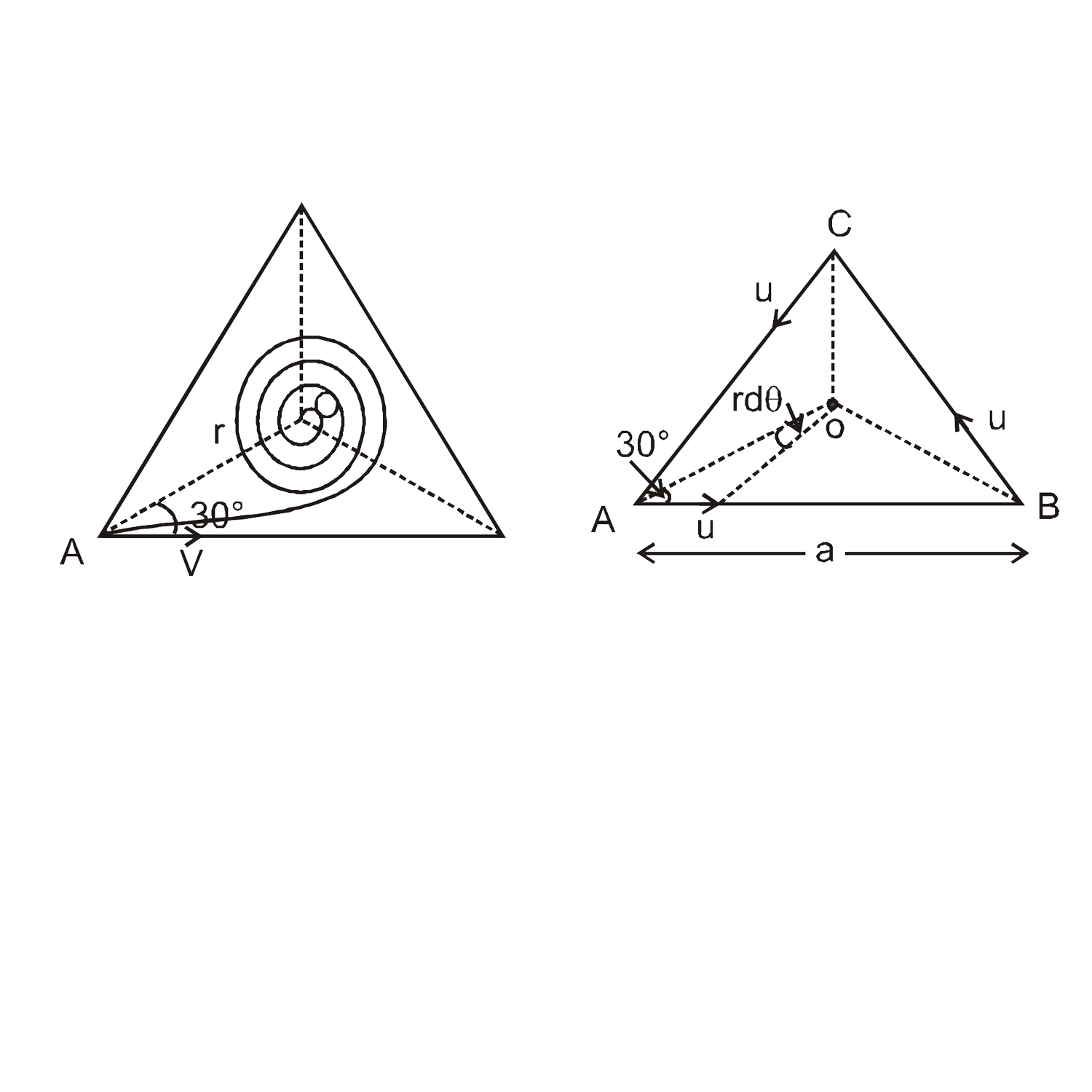
drdt=−vcos30∘=−√32V
rdthηdt=vsin30∘=√2
1rdrdthη=−√3
r∫r0drr=−√3θ∫0⇒r=r0e−√30
When A completes are revolution θ=2π
Time taken t=r0(1−e−2√3π)√3v/2
Distance travelled D=vt=2r0√3(1−e−2√3π)
D=2a3(1−e−2√3π)
Topper's Solved these Questions
Similar Questions
Three boys A,B and C are situated at the vertices of an equilateral triangle of side d at t=0. Each of the boys moves with constant speed v. A always moves towards C and C towards A, At what time and where they meet each other?
View SolutionThree particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
View Solution
Knowledge Check
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
At=dvBt=3d2vCt=2d3vDt=0Three particles A,B and C and situated at the vertices of an equilateral triangle ABC of side of length l at time t=0,Each of the particles move with constant speed u. A always has its velocity along AB,B along BC and C along CA.
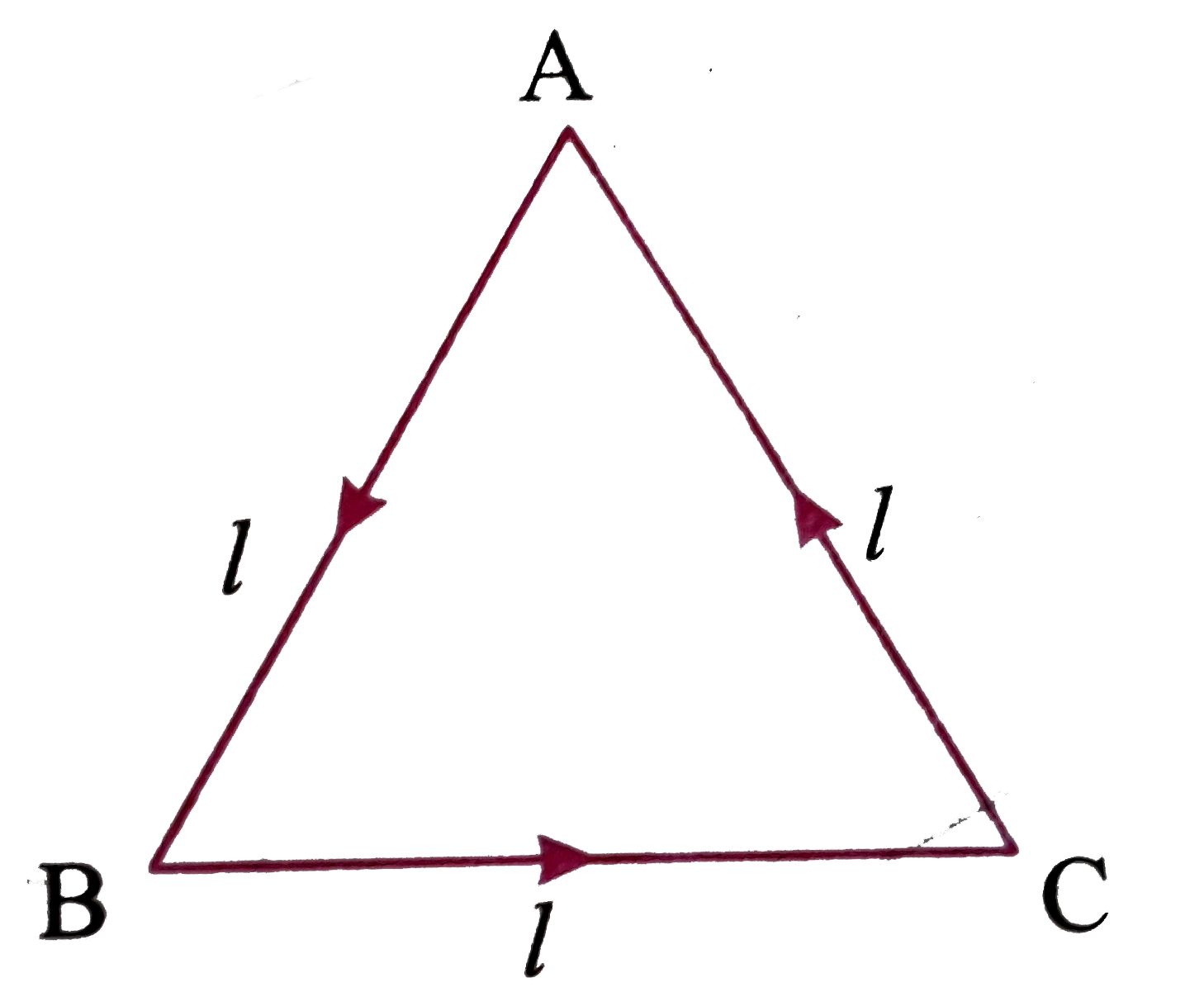AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2Three particles A(50g),B(100g) and C(150g) are placed at vertices of an equilateral triangle as shown in figure. Then the coordinates of center of mass of system is :
_2019_CBT8_E01_014_Q01.png)
A(712√34)cmB(√34,712)cmC(716√38)cmD(√38,716)cm
Three particle A, B and C situated at the vertices of an equilateral triangle starts moving simultaneously at a constant speed "v" in the direction of adjacent particle, which falls ahead in the anti-clockwise direction. If "a" be the side of the triangle, then find the time when they meet
View SolutionThree insects A,B and C are situated at the vertices of an equillateral triangle of side 1. the insect A heads towards B,B towards C,C towards A with constant speeds v such that they always remain at the vertices of an equilateral triangle. Find the (a) time of their meeting (b) equation of path traced by one insect relative to the other.
View SolutionThree particles are located at the corners of an equilateral triangle of side a=√3m. The particles start moving with a constant speed v=2ms such that the particle initially at A always heads towards the particle initially at B. and the particle at B heads for the particle at C and the particle at C heads for the particle-at A. The magnitude of initial acceleration (in ms2 ) of the particle at ⋅C is
View SolutionEight particles A,B,C,D,E,F,G and H are originally located at the vertices of regular octagon of side length l.At time t=0 second all of them begin to move with constant speed v such that A moves towards B, B moves towards C And so on.They will meet after a time interval of
View SolutionThree identical particles are located at the vertices of an equilateral triangle. Each particle moves along a meridian with equal speed towards the centroid and collides inelastically.
View Solution