Three particle A, B and C situated at the vertices of an equilateral triangle starts moving simultaneously at a constant speed "v" in the direction of adjacent particle, which falls ahead in the anti-clockwise direction. If "a" be the side of the triangle, then find the time when they meet

Video Solution

Text Solution

Verified by Experts

Here, particle "A" follows "B", "B" follows "C" and "C" follows "A". The direction of motion of each particle keeps changing as motion of each particle is always directed towards other particle. The situa- tion after a time "t" is shown in the figure with a possible outline of path followed by the particles before they meet

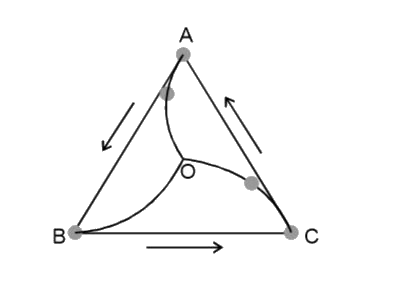
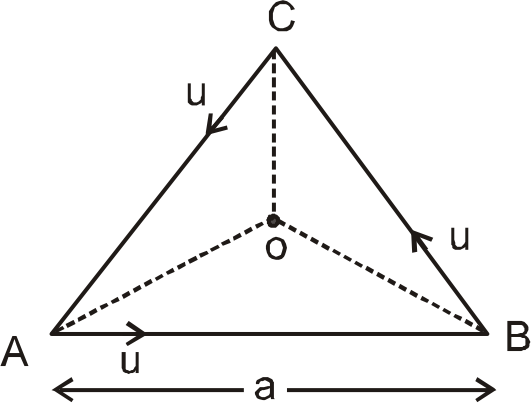
This problem appears to be complex as the path of motion is difficult to be defined. But, it has a simple solution in component analysis. Let us consider the pair "A" and "B". The initial component of velocities in the direction of line joining the initial position of the two particles is "v" and "vcos $θ$ " as shown in the figure here :

The component velocities are directed towards eachother. Now, considering the linear (one dimensional) motion in the direction of AB, the relative velocity of "A" with respect to "B" is :
$v_{A B} = v_{A} - v_{B}$
$v_{A} B = v - (- v cos θ) = v + cos θ$
In equilteral triangle , $θ = 60^{\circ}$
$V_{A B} = v + {cos 60}^{\circ} = v + \frac{v}{2} = \frac{3 v}{2}$
The time taken to cover the displacement "a" i.e. the side of the triangle
$t = \frac{2 a}{3 v}$

Updated on:21/07/2023