Three particles of masses 0.2kg,0.3kg and 0.4kg are situated at the vertices A,B and C of a right angled traingle ABC with ∠A=90∘,AB=2cm along X-axis and BC=2.5cm. Find the distance of centre of mass from A.
To find the distance of the center of mass from point A in the given problem, we will follow these steps:
Step 1: Define the coordinates of the points
We have a right-angled triangle ABC with:
- Mass m1=0.2kg at point A (0, 0)
- Mass m2=0.3kg at point B (0, 2) (since AB = 2 cm along the Y-axis)
- Mass m3=0.4kg at point C (1.5, 2) (we will find the x-coordinate of C using the Pythagorean theorem)
Step 2: Find the coordinates of point C
Using the Pythagorean theorem:
BC2=AB2+AC2
Given BC=2.5cm and AB=2cm:
(2.5)2=(2)2+AC2
6.25=4+AC2
AC2=6.25−4=2.25
AC=√2.25=1.5cm
Thus, the coordinates of point C are (1.5, 2).
Step 3: Calculate the center of mass
The formula for the center of mass Rcm of a system of particles is given by:
Rcm=m1R1+m2R2+m3R3m1+m2+m3
Where R1,R2,R3 are the position vectors of the masses.
Substituting the values:
- R1=(0,0)
- R2=(0,2)
- R3=(1.5,2)
We calculate:
Rcm=0.2(0,0)+0.3(0,2)+0.4(1.5,2)0.2+0.3+0.4
Calculating the numerator:
=(0,0)+(0,0.6)+(0.6,0.8)0.9
=(0.6,1.4)0.9
=(0.6667,1.5556) or (23,149)
Step 4: Find the distance from A
The distance d from point A (0, 0) to the center of mass is given by:
d=√x2+y2
Substituting the coordinates of the center of mass:
d=√(23)2+(149)2
Calculating:
=√49+19681
Finding a common denominator:
=√3681+19681=√23281=√2329
Final Answer
The distance of the center of mass from point A is:
d=√2329≈2.4 cm
We have a right-angled triangle ABC with:
- Mass m1=0.2kg at point A (0, 0)
- Mass m2=0.3kg at point B (0, 2) (since AB = 2 cm along the Y-axis)
- Mass m3=0.4kg at point C (1.5, 2) (we will find the x-coordinate of C using the Pythagorean theorem)
Using the Pythagorean theorem:
BC2=AB2+AC2
Given BC=2.5cm and AB=2cm:
(2.5)2=(2)2+AC2
6.25=4+AC2
AC2=6.25−4=2.25
AC=√2.25=1.5cm
Thus, the coordinates of point C are (1.5, 2).
The formula for the center of mass Rcm of a system of particles is given by:
Rcm=m1R1+m2R2+m3R3m1+m2+m3
Where R1,R2,R3 are the position vectors of the masses.
- R1=(0,0)
- R2=(0,2)
- R3=(1.5,2)
Rcm=0.2(0,0)+0.3(0,2)+0.4(1.5,2)0.2+0.3+0.4
Calculating the numerator:
=(0,0)+(0,0.6)+(0.6,0.8)0.9
=(0.6,1.4)0.9
=(0.6667,1.5556) or (23,149)
The distance d from point A (0, 0) to the center of mass is given by:
d=√x2+y2
Substituting the coordinates of the center of mass:
d=√(23)2+(149)2
Calculating:
=√49+19681
Finding a common denominator:
=√3681+19681=√23281=√2329
The distance of the center of mass from point A is:
d=√2329≈2.4 cm
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE A
2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES
62 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Three particles of masses 0.2kg,0.3kg and 0.4kg are situated at the vertices A,B and C of a right angled traingle ABC with ∠A=90∘,AB=2cm along X-axis and BC=2.5cm. Find the distance of centre of mass from A.
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
View Solution
Knowledge Check
Three particles of masses 1kg,32kg,and2kg are located at the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
A(5a9,2a3√3)B(2a33,5a9)C(5a9,2a√3)D(2a√3,5a9)Three particles of masses 1 kg, 2 kg and 3 kg are situated at the corners of an equilateral triangle of side b in the x-y plane with mass 1 kg at the origin and 2 kg on the x-axis. The coordinates of the centre of mass are
A(7b12,3√3b12)B(3√3b12,7b12)C(b12,3√3b12)D(7b12,√3b12)
In a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
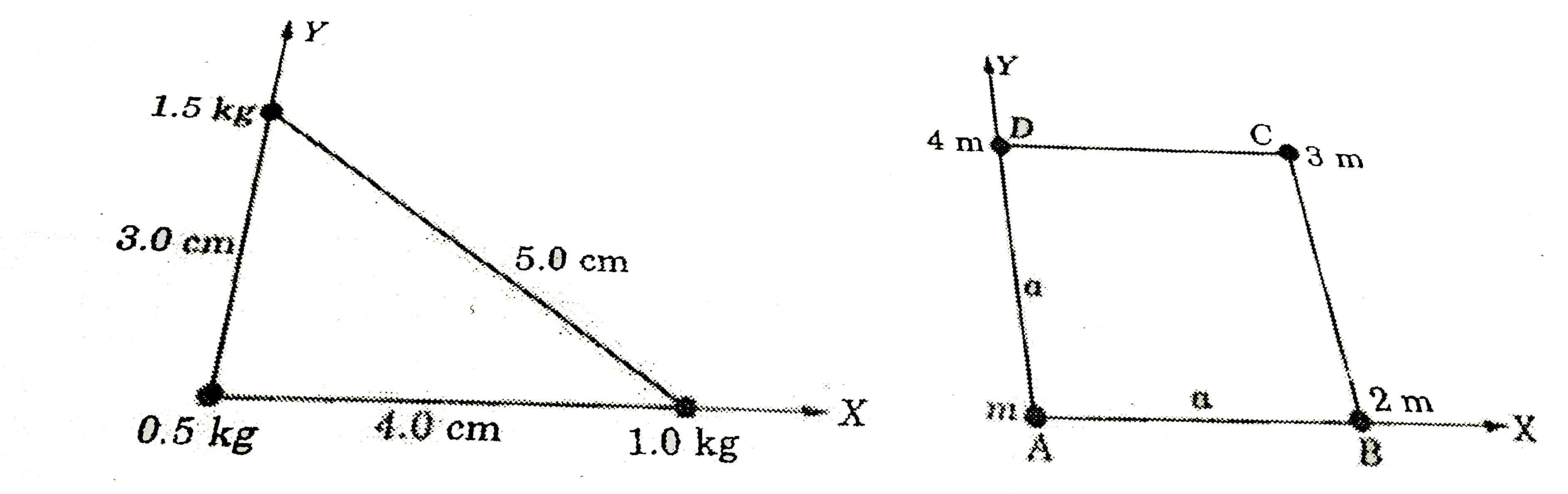
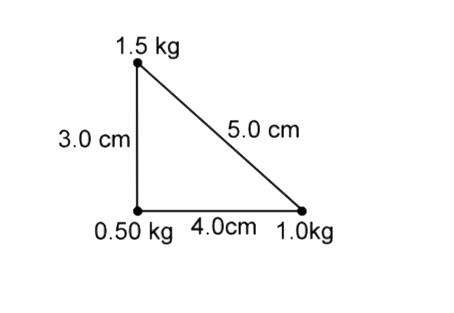
View SolutionThree particles of masses 0.5 kg, 1.0 kg and 1.5 kg are placed at the three corners of a right angled triangle of sides 3.0 cm, 4.0 cm and 5.0 cm as shown in figure. Locate the centre of mass of the system.
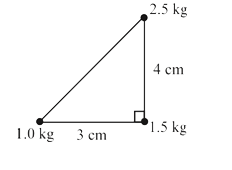
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
View SolutionThree particles of msses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre ofmass of the system.
View SolutionFour particles of mass 2 kg, 3kg, 4 kg and 8 kg are situated at the comers of a square of side length 2 m. The centre of mass may be given as
View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View Solution