A mass of 3kg descending vertically downwards supports a mass of 2kg by means of a light string passing over a pulley At the end of 5s the stringbreaks How much high from now the 2kg mass will go (g=9.8m/2).
9.8m
19.6m
2.45m
4.9m
The correct Answer is:d
Acceleration of the system before the string
breaks a=net pulling forcetotal mass=3g−2g(3+2)=g5
After 5s, velocity of the system,
υ=at=g5×5=gm/s
Required height h=υ22g=g×g2g=g2
=9.82=4.9m .
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Integer Type Questions
Explore 7 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Problems for practice
Explore 112 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
Two masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
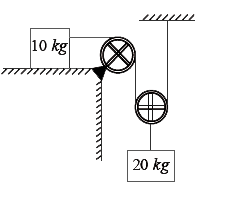
View SolutionTwo bodies of masses 4kg and 3kg respectively are connected by a light string passing over a smooth frictionless pulley Calculate the acceleration of the masses and tension in the string .
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A188 NB2=368 NC288 ND168 N
A188 NB2=368 NC288 ND168 NTwo bodies of mass 3kg and 4kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2Two bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
A4.9m/s2B2.45m/s2C1.4m/s2D9.5m/s2
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View SolutionTwo bodies of mass 5 kg and 7 kg are suspended at the ends of massless string passing over frictionless pulley. The acceleration of the system.
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionTwo masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is

View Solution

