A body m1 of mass 10 kg is placed on a smooth horizontal table It is connected to a string which passes over a frictionless pulley and carries at the other end , a body m2 of mass 5 kg What acceleration will be produced in the bodies when the nail fixed on the table is removed ? what will be the tension in the string during the motion of the bodies ? What when the bodies stop ? (g= 9.8 N ? kg ) .
To solve the problem step by step, we will analyze the forces acting on both masses and apply Newton's second law of motion.
Step 1: Identify the system and forces acting on each mass
- Mass m1=10kg is on a smooth horizontal table.
- Mass m2=5kg is hanging vertically.
- When the nail is removed, m2 will accelerate downward due to gravity, and m1 will accelerate horizontally.
Step 2: Write the equations of motion for both masses
For mass m2:
- The forces acting on m2 are:
- Weight W2=m2g=5×9.8=49N (downward)
- Tension T in the string (upward)
Using Newton's second law:
m2g−T=m2a(1)
Substituting the values:
49−T=5a(1)
For mass m1:
- The only horizontal force acting on m1 is the tension T.
Using Newton's second law:
T=m1a(2)
Substituting the values:
T=10a(2)
Step 3: Solve the equations simultaneously
Now we have two equations:
1. 49−T=5a
2. T=10a
Substituting equation (2) into equation (1):
49−10a=5a
Combining like terms:
49=15a
Solving for a:
a=4915≈3.27m/s2
Step 4: Find the tension in the string during motion
Now, substitute a back into equation (2) to find T:
T=10a=10×4915=49015≈32.67N
Step 5: Determine the tension when the bodies stop
When the bodies stop, the acceleration is 0, and the tension will equal the weight of m2:
T=m2g=5×9.8=49N
Summary of Results
- The acceleration of the bodies when the nail is removed is approximately 3.27m/s2.
- The tension in the string during the motion of the bodies is approximately 32.67N.
- The tension in the string when the bodies stop is 49N.
- Mass m1=10kg is on a smooth horizontal table.
- Mass m2=5kg is hanging vertically.
- When the nail is removed, m2 will accelerate downward due to gravity, and m1 will accelerate horizontally.
For mass m2:
- The forces acting on m2 are:
- Weight W2=m2g=5×9.8=49N (downward)
- Tension T in the string (upward)
m2g−T=m2a(1)
Substituting the values:
49−T=5a(1)
- The only horizontal force acting on m1 is the tension T.
Using Newton's second law:
T=m1a(2)
Substituting the values:
T=10a(2)
Now we have two equations:
1. 49−T=5a
2. T=10a
49−10a=5a
Combining like terms:
49=15a
Solving for a:
a=4915≈3.27m/s2
Now, substitute a back into equation (2) to find T:
T=10a=10×4915=49015≈32.67N
When the bodies stop, the acceleration is 0, and the tension will equal the weight of m2:
T=m2g=5×9.8=49N
- The acceleration of the bodies when the nail is removed is approximately 3.27m/s2.
- The tension in the string during the motion of the bodies is approximately 32.67N.
- The tension in the string when the bodies stop is 49N.
Topper's Solved these Questions
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:conceptual problmes
Explore 45 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Very short answer questions
Explore 73 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:1 NCERT Comprehension
Explore 4 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
Similar Questions
A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View SolutionA mass m rests on a horizontal table. It is attached to a light inextensible string which passes over a smooth pulley and carries a mass m at the other end. If the mass m is raised vertically through a distance h and is then dropped, what is the speed with which the mass 2m begins to rise?

View Solution
Knowledge Check
A body of mass 10 kg is placed on the horizontal smooth table (see given figure). A string is tied with it which passes over a frictionless pulley. The other end of the string is tied with a body of mass 5 kg. When the bodies move, the acceleration produced in them, is
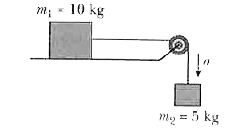 A9.8 m/s2B4.8 m/s2C4.25 m/s2D3.27 m/s2
A9.8 m/s2B4.8 m/s2C4.25 m/s2D3.27 m/s2A block A of mass 7 kg is placed on a frictionless table. A thread tied to it passes over a frictionless pulley and carries a body B of mass 3 kg at the other end. The acceleration of the system is (given g=10ms−2)
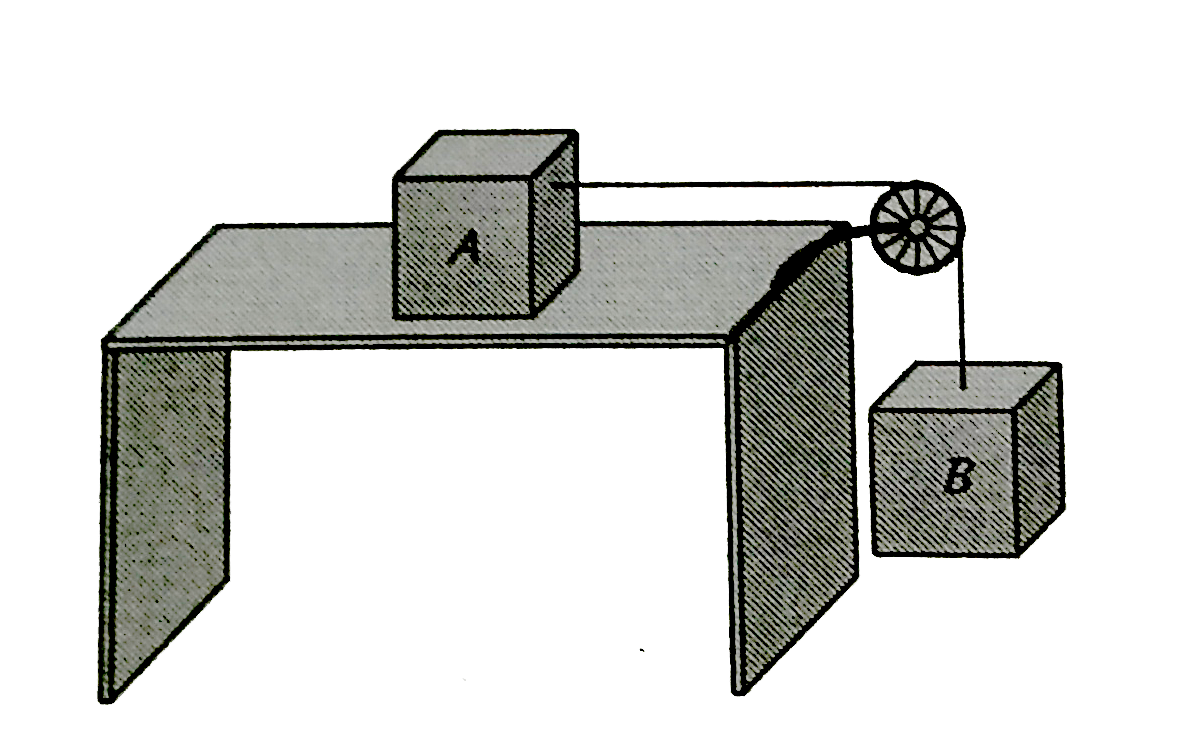 A100ms−2B3ms−2C10ms−2D30ms−2
A100ms−2B3ms−2C10ms−2D30ms−2A block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pully at the edge of the table and from its other end another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is H. When the block A is sliding on the table, the tension in the string is
View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
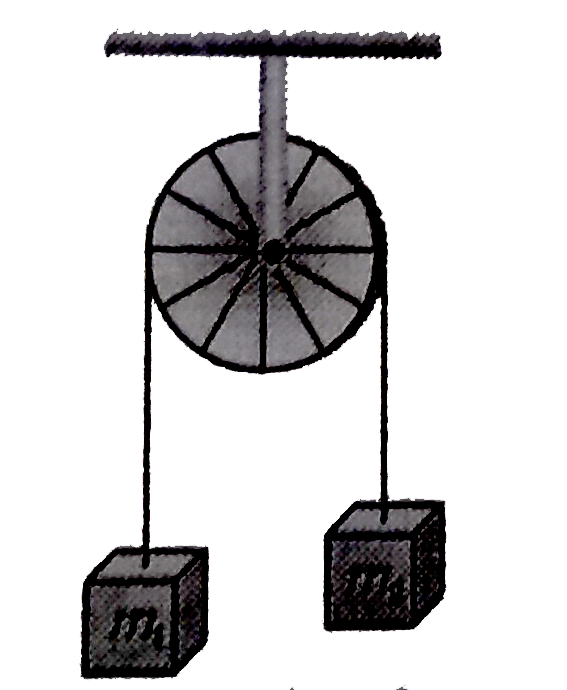
View SolutionTwo masses of 8kg and 4kg are connected by a string as shown in figure over a frictionless pulley.The acceleration of the system is

View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
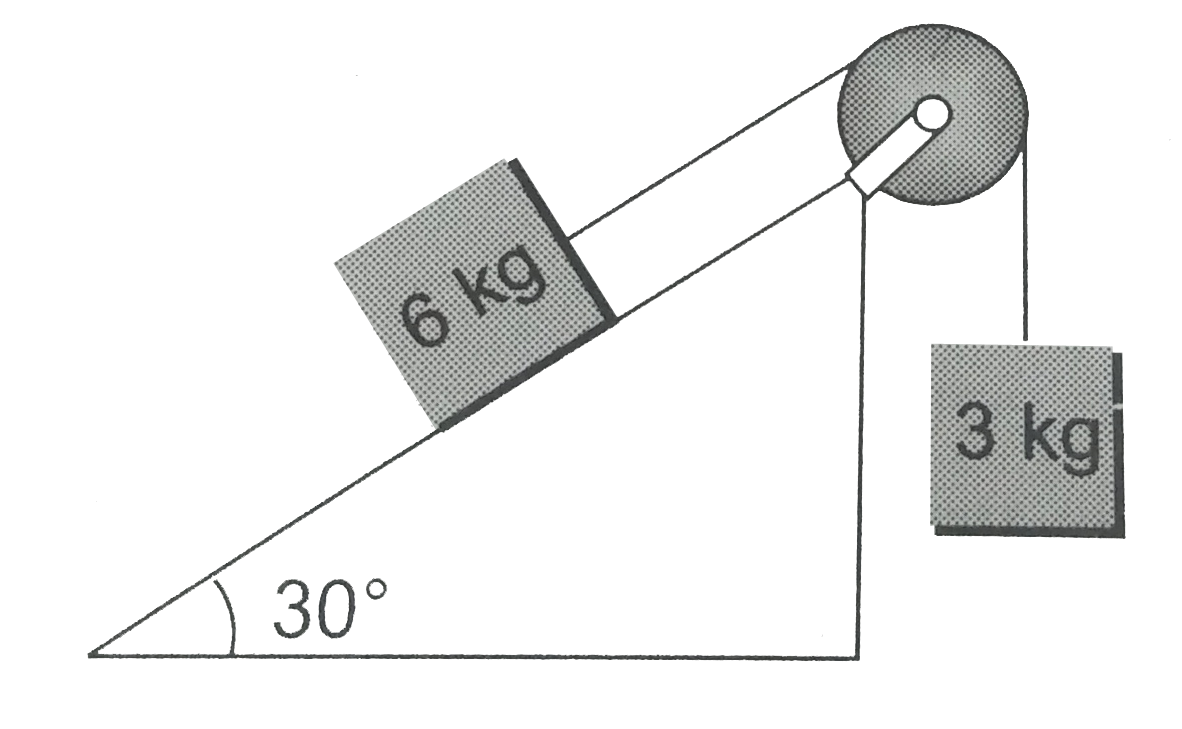
View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View Solution

