A mass m rests on a horizontal table. It is attached to a light inextensible string which passes over a smooth pulley and carries a mass m at the other end. If the mass m is raised vertically through a distance h and is then dropped, what is the speed with which the mass 2m begins to rise?

Velocity of the mass m just before string becomes tight.

v=√2gh ……….i
Using impulse = change in momentum
For mass 2m
J=2mv1……….ii
For mass m
mv−J=mv1 ………..iii
Solving eqn i , ii and iii we get v=√2gh3
Topper's Solved these Questions
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Solved Examples
Explore 13 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICSChapter:CENTRE OF MASSExercise:Exercise 1.1
Explore 20 Videos
- CALORIMETRYBook:CENGAGE PHYSICSChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
Similar Questions
Two particle A and B, of mass 3mand2m respectively, are attached to the ends of a light inextensible string which passes over a smooth fixed pulley of negligible mass. After the system is released and A falls through a distance L, it hits a horizontal inelastic table so that its speed is immediately reduced to zero. Assume that B never hits the table or the pulley. Find
(a) the time for which A is resting on the table after the first collision and before it is jerked off,
(b) the difference between the total kinetic energy of the system immediately before A first hits the table and total kinetic energy immediately after A starts moving upwards for the first time. Explain the loss in kinetic energy.

View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution
Knowledge Check
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gA block of mass m1 lies on a smooth horizontal table and is connected to another freely hanging block of mass m2 by a light inextensible string passing over a smooth fixed pulley situated at the edge of the table. Initially the system is at rest with m1 a distance d from the pulley. Then the time taken for m1 to reach the pulley is.
 Am2gm1+m2B√2d(m1+m2)m2gC√2m2d(m1+m2)gDNone of thess
Am2gm1+m2B√2d(m1+m2)m2gC√2m2d(m1+m2)gDNone of thessA smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
 AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
A block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
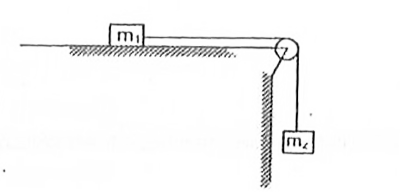
View SolutionA block of mass M is placed on a horizontal surface. It is tied with an inextensible string that passes through ideal pulleys. A mass m is connected to the pulley as shown. For what value of m, the block M will accelerate towards the fixed pulley ?
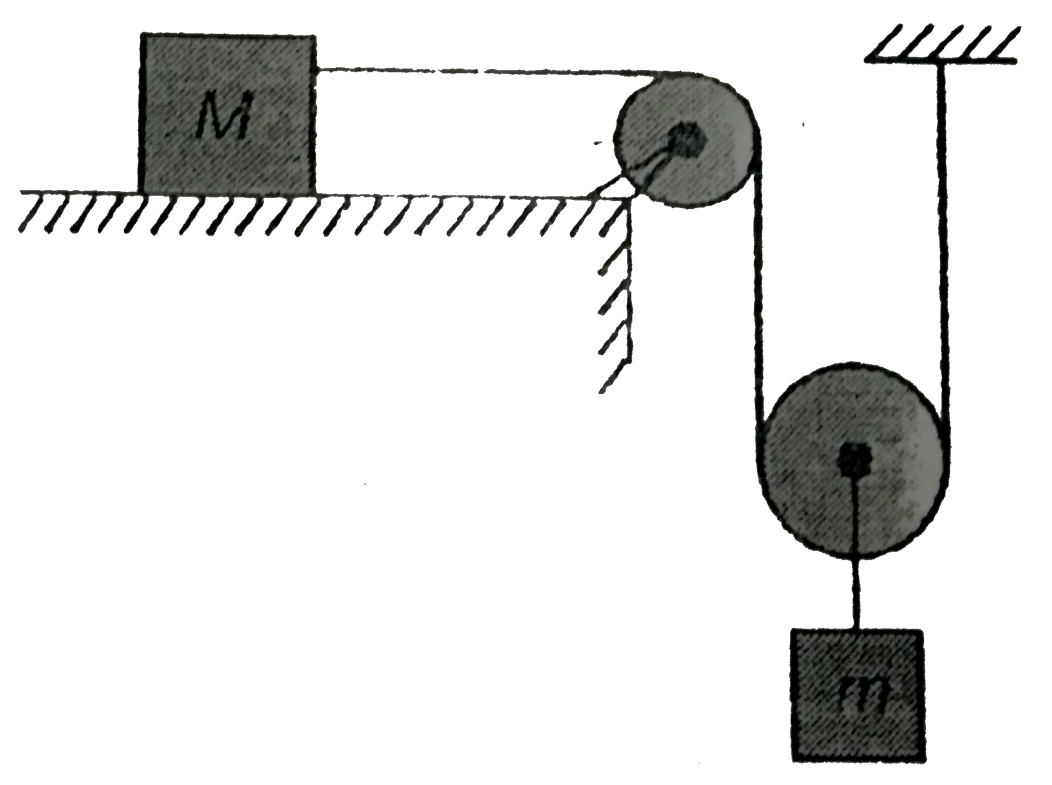
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
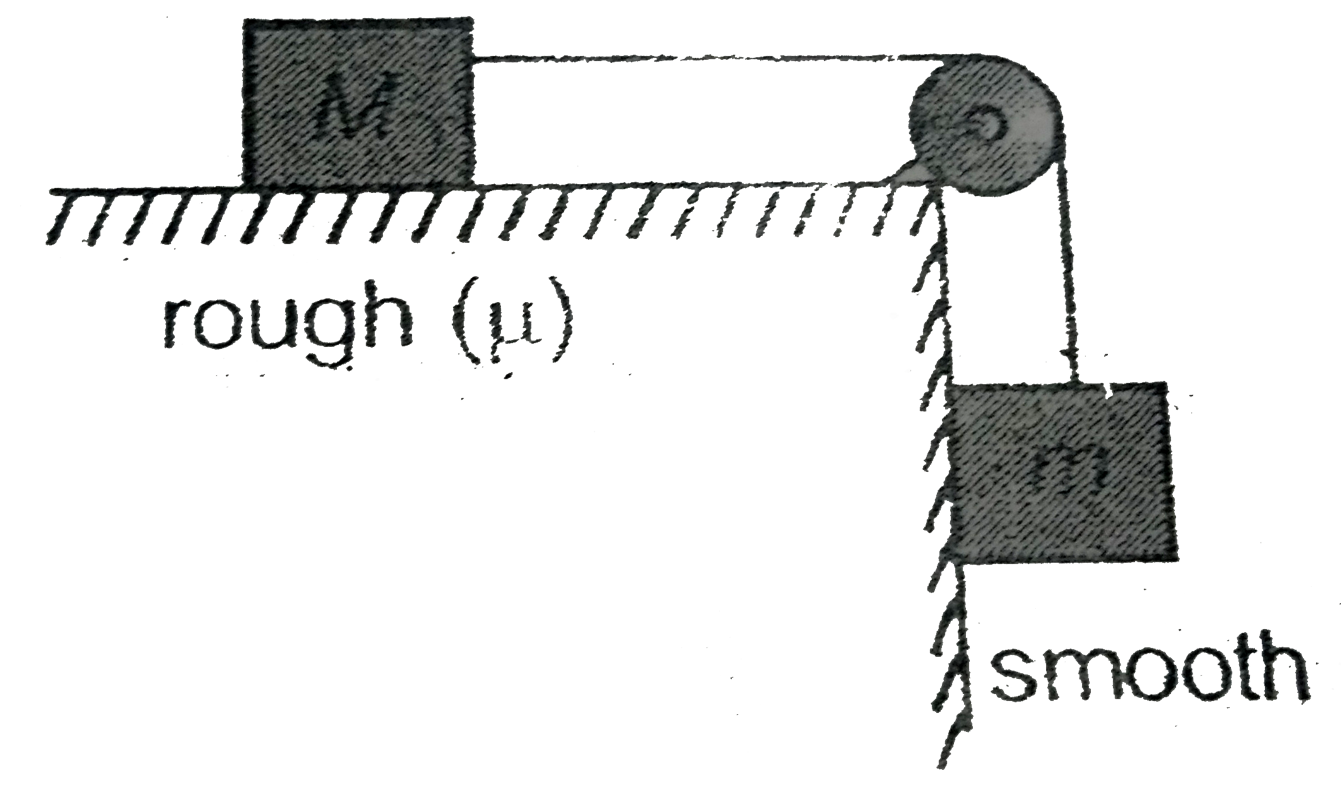
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionA block of mass 2 m hangs by an inextensible light string that passes over a smooth pulley. Another mass m hangs from the other end of the string and is connected to a vertical massless spring. The system is stationary. Just after the string is cut, the accelerations of m and 2m, respectively, are -

View Solution

