Question

The length of a seconds hand in watch is $1cm.$ The change in velocity of its tip in $15s$ is

Options

A. zero
B. ` pi //(30 sqrt 2)`
C. ` pi // 30`
D. ` 2 pi // ( 30 sqrt 2 )`

Answer

D

Explanation

The angle described at the centre by the length of seconds hand of a watch in ` 15 seconds = 90^@` ltBrgt ` = pi //2 ` radians Tig. 2 (CF) . 65 .
.
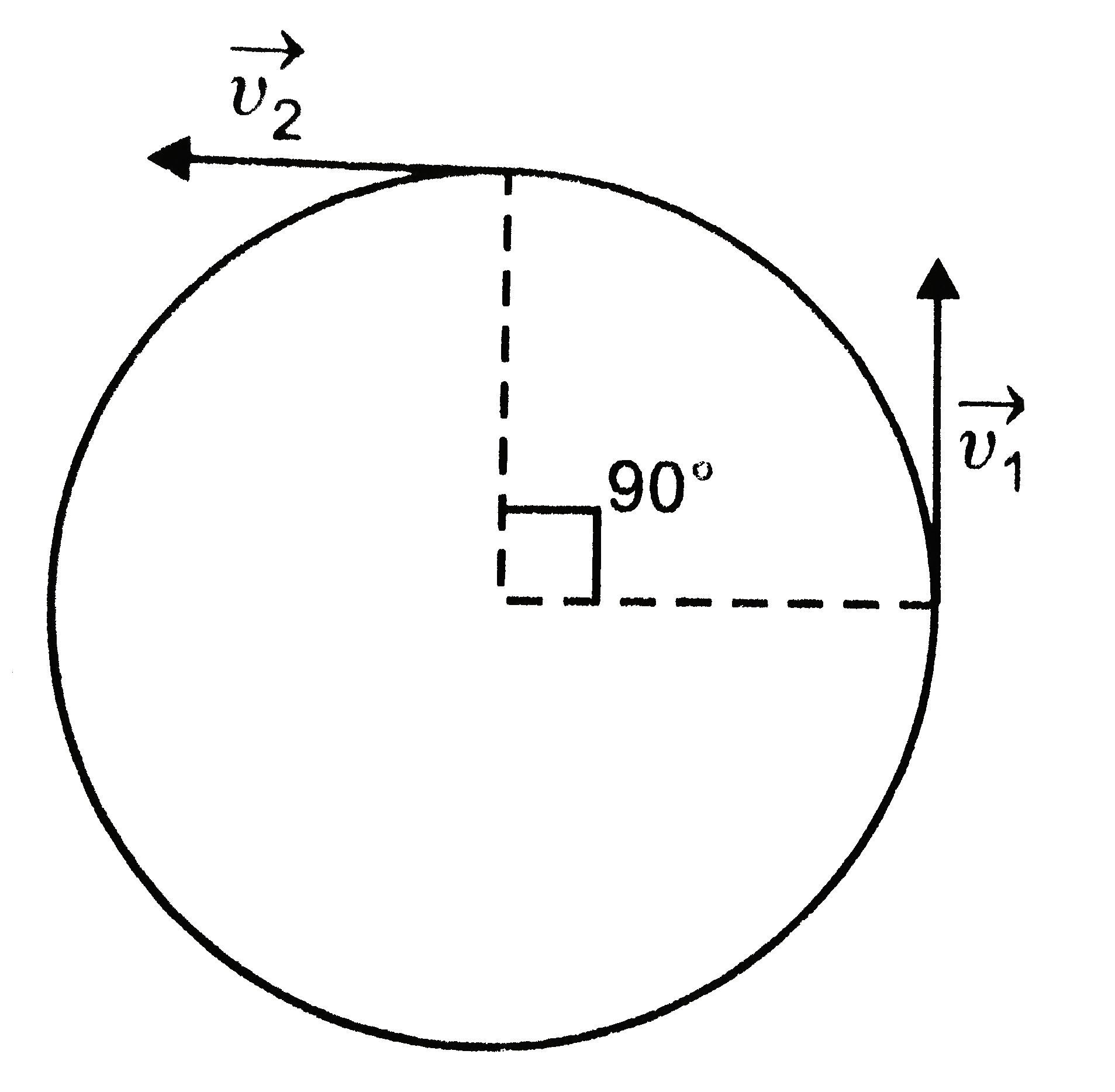Lenear speed , ` v = r omega = r theta //t` ltBrgt Magnitude of change in velocity in ` 15 sec
` | Delta vec v| = | vec -2 - vec v_1 | = sqrt( v_^2^1 + v_1^2)` ltBrgt ` = sqrt ( v^2 +v^2 ) = sqrt 2 v = sqrt 2 (pi)/(30) = (2pi)/(30) = 92 pi) /(30 sqrt 2) cm //s` .