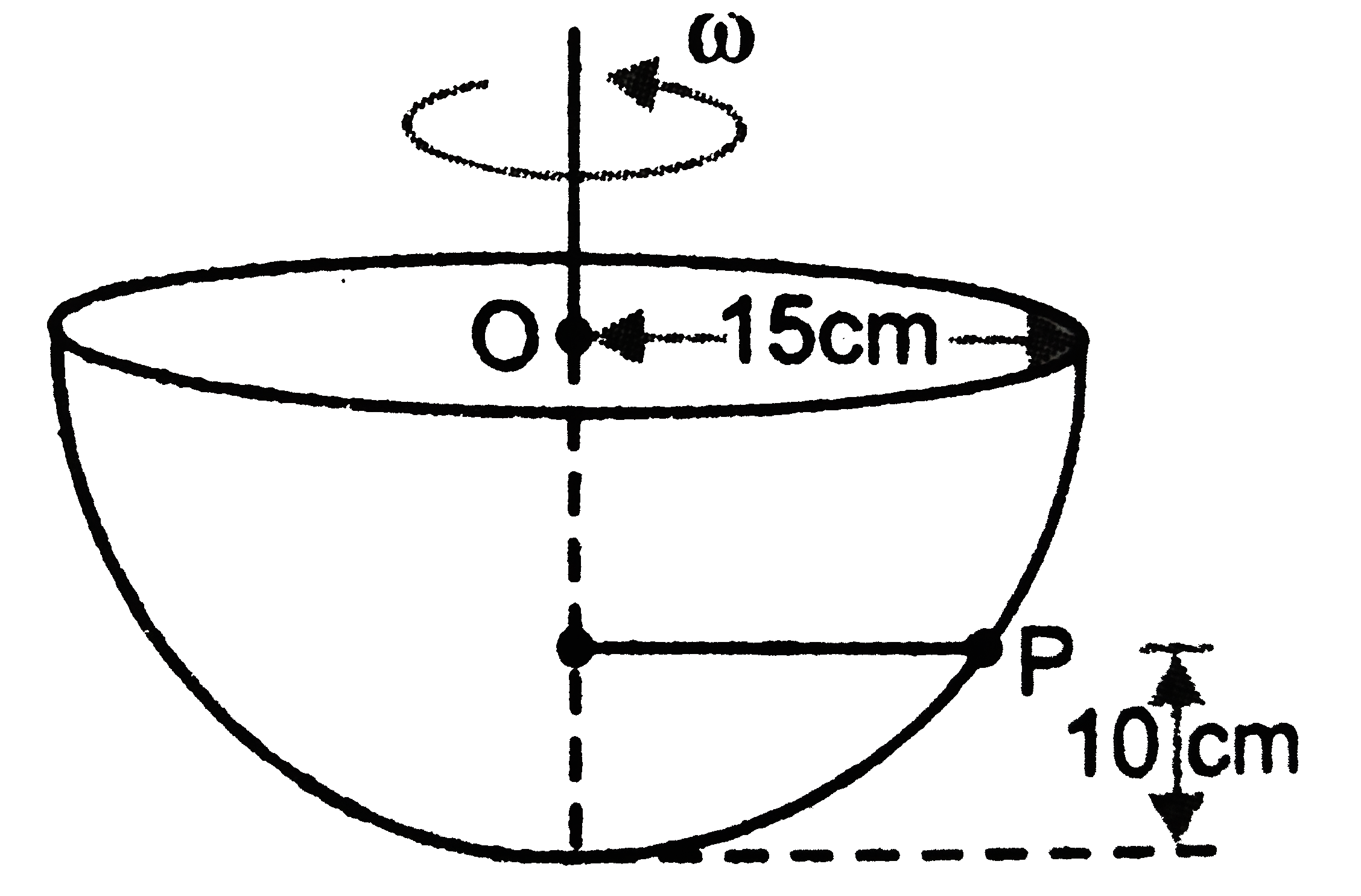
A smooth hemispherical bowl 30cm diameter potates with a constatn angular velocity ω, about its vertical axis of symmetry. A particle at (P) of weighing 5kg, is onserved to remantn at rest telative to the bowal at a height 10cm above teh base, Fig. 1 (CF) . 34. The magnitude fo speed of rotation of the bowl is
 .
.
15rad/s
23rad/s
14rad/s
16rad/s
The correct Answer is:C
LetR be the force exerted by the bowl in the particle. It will be as a reactional force (R ). Various forces acting on particle at (P) will be (i) weight
Mg (downwards ) (ii) R (Normal reaction ) along (PO).
 .
.
Resolving (R ) into tis two rectangular components we have Rsinθ acts vertically wpards and Rcosthea acts horizontally along PQ As horizontal component Rcosθ will proved required centripetal force.
∴ R cos theta = ma_c<br>[ac→centripηla≤ration]
Rcosθmrω2 or ω=√Rcosθmr
cosθ=θrOP=r0.15
[:. R sin theta = mg
R = (mg)/(sin theta)= (mg)/(OQ//OP) = ( 5 xx 9.8)/(0.05 //0 15/
(R = 15 xx 9.8 N)]
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 NCERT multiple Choice
Explore 10 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 NCERT Integer type
Explore 4 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 NCERT multiple
Explore 15 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
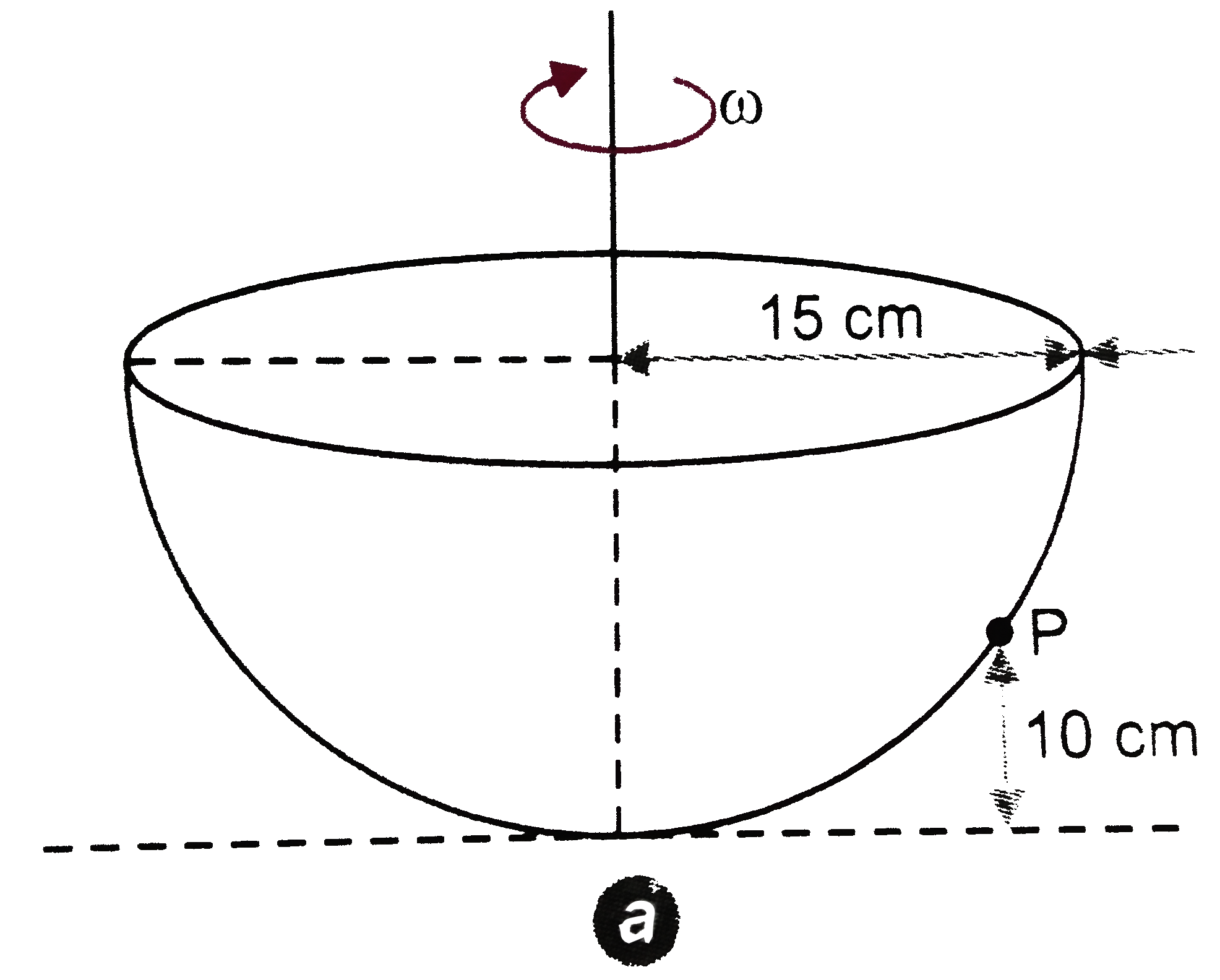
A smooth hemispherical bowl 30cm diameter, rotates with a constant angular velocity ω, about its vertical axis of symmetry Fig. 2 (APC) . 2 (a) . A particle at (P) of weighing 5kg is observed to remain at rest relative to the bowl at a height 10cm above the base. Find the magnitude of the force exerted by the bowl on the particle and speed of rotation of the bowl.
 .
.
View SolutionA rough horizontal plate rotates with a constant angular velocity w about its vertical axis. A particle of mass m lies on the plate at a distance 5a4 from the axes. If the coefficient of friction is 13 and the particle remains at rest relative to the plane, show that w≤√4g15a. The particle is now connected to axis by a horizontal elastic string, of natural length a and modulus 3 mg. If the particle remains at rest relative to the plate and at a distance 5a4, show that the greatest possible angular velocity is √1315.ga and find the least possible velocity.
View Solution
Knowledge Check
A uniform solid cone of mass m, base radius ‘R’ and height 2R, has a smooth groove along its slant height as shown in figure. The cone is rotating with angular speed ω, about the axis of symmetry. If a particle of mass ‘m’ is released from apex of cone, to slide along the groove, then angular speed of cone when particle reaches to the base of cone is
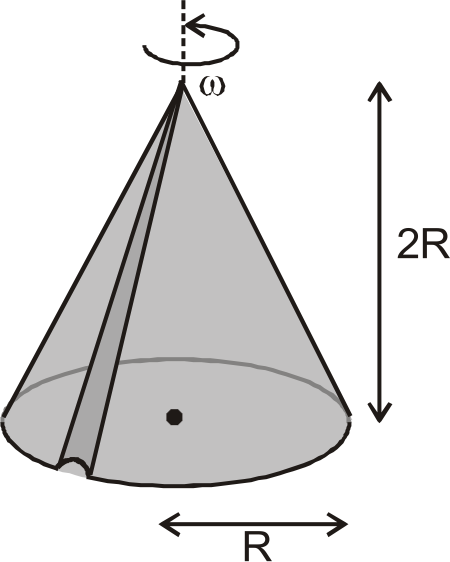 A3ω13B4ω13C5ω13D9ω13
A3ω13B4ω13C5ω13D9ω13A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
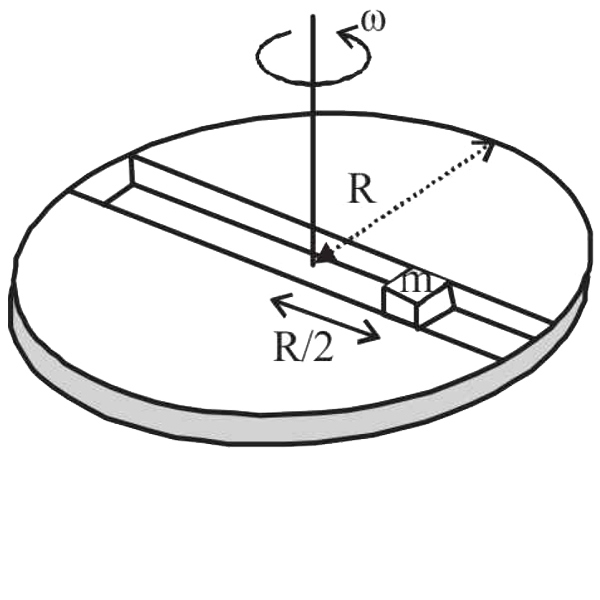
The distance r of the block at time isA(a) R4(eωt+e−ωt)B(b) R2cosωtC(c) R4(e2ωt+e−2ωt)D(d) R2cos2ωtA frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of non=inertial frame of reference. The relationship between the force →Frot experienced by a particle of mass m moving on the rotating disc and the force →F∈ experienced by the particle in an inertial frame of reference is
→Frot=→Fin+2m(→vrot×→ω)+m(→ω×→r)×→ω.
where →vrot is the velocity of the particle in the rotating frame of reference and →r is the position vector of the particle with respect to the centre of the disc.
Now consider a smooth slot along a diameter fo a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis (→ω=ωˆk). A small block of mass m is gently placed in the slot at →r(R/2)ˆi at t=0 and is constrained to move only along the slot.
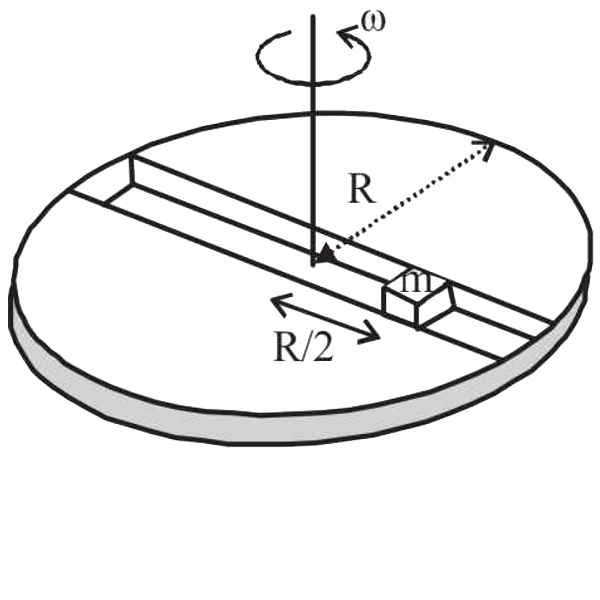
The net reaction of the disc on the block isA(a) 12mω2R(e2ωt−e−2ωt)ˆj+mgˆkB(b) 12mω2R(eωt−e−ωt)ˆj+mgˆkC(c) −mω2Rcosωtˆj−mgˆkD(d) mω2Rsinωˆj−mgˆk
A small body of mass m=0.30kg starts sliding down from the top of a smooth sphere of radius R=1.00m. The sphere rotates with a constant angular velocity ω=6.0rad/s about a vertical axis passing through its centre. Find the centrifugal force of inertia and the Coriolis force at the moment when the body breaks off the surface of the sphere in the reference frame fixed to the sphere.
View SolutionA horizontal disc rotates with a constant angular velocity ω=6.0rad/s about a vertical axis passing through its centre. A diameter of the disc with a velocity v′=50cm/s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r=30cm from the rotation axis.
View SolutionA horizontal smooth rod AB rotates with a constant angular velocity ω=2.00rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m=0.50g moves along the rod from the point A with the initial velocity v0=1.00m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to rotating rod) at the moment when the sleeve is located at the distance r=50cm from the rotation axis.
View SolutionA particle is placed inside a hemispherical bowl which rotates about its vertical axis with constant angular speed ω. It is just prevented from sliding down when the line joining it to the centre of the hemisphere is 45∘ with the vertical. The radius of the bowl is 10√2m. The coefficient of friction between the particle and the bowl is 0.5 and g=10ms−2. Find the magnitude of ω.
View SolutionA hemispherical bowl of radius R is rotating about its own axis (which is vertical) with an angular velocity ω . A particle on the frictionless inner surface of the bowl is also rotating with the same ω . The particle is a height h from the bottom of the bowl.
(i) Obtain the relation between h and ω _________
(ii) Find minimum value of ω needed, in order to have a non-zero value of h _____________ .
View Solution

