A skier starts from rest at the top of a ski slope and skis downhill. Find the skier's speed after her elevation decreases by 10m, assuming no work is done by friction or air resistance.
Change in PE of the skier when her elevation decreases by 10m,i.e.,Ep=mgh Since no work is done against friction or air resistance, Ep is converted into the kinetic energy
(12μψlon2) of the skier, i.e., Ep=12mυ2ormgh=12mυ2
or υ=√2gh=√2(9.8)(10)=14m/s (as h = 10m)
Topper's Solved these Questions
- WORK AND ENERGYBOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Continuous Assessment I oral testing
10 Videos
- WORK AND ENERGYBOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - II Quiz Testing
5 Videos
- WORK AND ENERGYBOOK - PRADEEPCHAPTER - WORK AND ENERGYEXERCISE - Continuous Assessment
24 Videos
- SOUNDBOOK - PRADEEPCHAPTER - SOUNDEXERCISE - Model Test (sec - B)
12 Videos
Similar Questions
A trolley car starts from rest at the top of a hill as shown in figure -3.9 and moves down the curved track. Determine its speed as it reaches the bottom. Assume that the work done by frictional forces is negligible.
View SolutionA skier starts from the top of a hill with speed 5m/s and slides down the hill of vertical height 60 m as shown. Neglect friction. Find his speed at the bottom.

View Solution
Knowledge Check
A skier leaves the top of a slope with an initial speed of 5.0 m/s. Her speed at the bottom of the slope is 13 m/s. What is the height of the slope ?
A1.1mB4.6mC6.4mD7.3mA skier starts from rest at point A and slides donw the hill without turning or breaking. The friction coefficient is μ When he stops at point B, his horizontal displacement is S. whalt is the height difference between points A and B?
(The velocity of the skier is small so that the additional pressure on the snow due to the curvature can vbe neglected. Neglect also the friction of air and the dependence of μ on the velocity of the skier)Ah=μSBh=μSCh=2μSDh=μS2A 25 kg crate starting from rest at the top slides down a plane that makes an angle of 30∘ with the horizontal . Whe it reaches the bottom of the 10 m long slide , its velocity is 8 m/s . The work done by the fore of friction is closest to a value of :
A17×102JB8.5×102JC6.5×102JD4.5×102J
A body of mass m starts from rest down a plane of length l at an angle θ with the horizontal. (a) find the body's speed at the bottom (b) How far will it slide horizontally on a similar surface after reaching the bottom of the incline. The coefficient of friction between the body and the plane is μ.
View SolutionOn a level road, a scooterist applies brakes to slow down from a speed of 10 m/s to 5 m/s. If the mass of the scooterist and the scooter be 150 kg, calculate the work done by the brakes. (Neglect air resistance and friction)
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
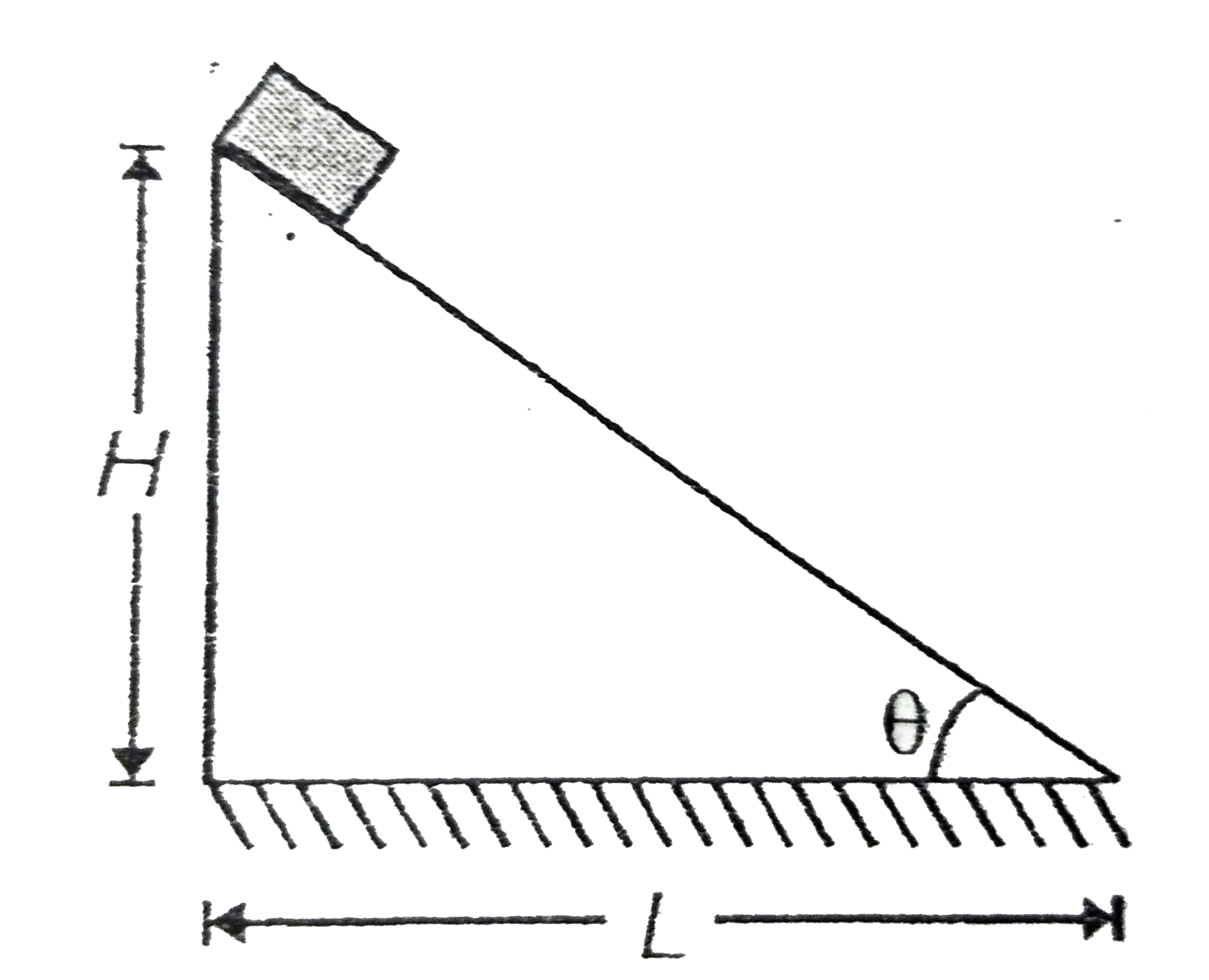
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10ms at the bottom of the inclined then work done by the friction force on the block will be
View Solution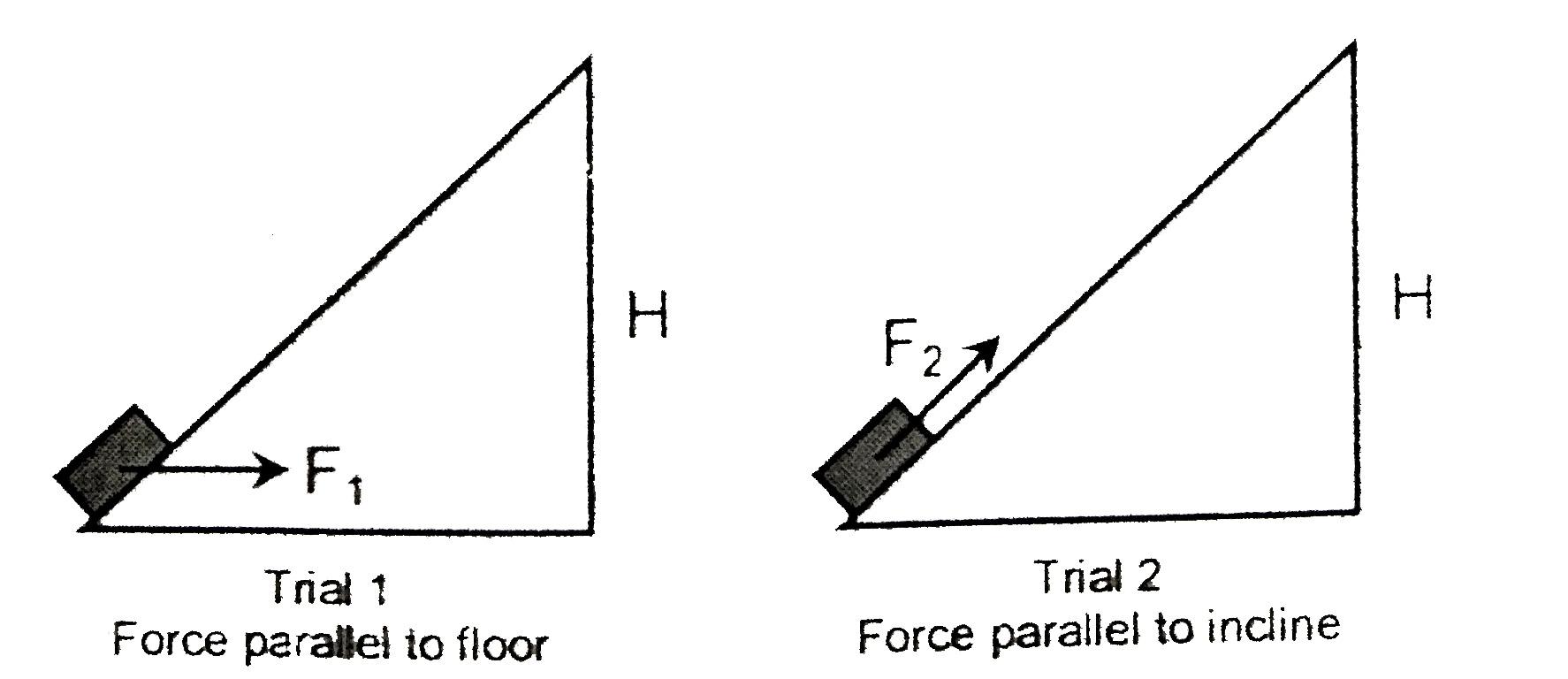
An object of mass M starts from rest at the bottom of a fixed incline of height H. A person decides to push the object up the incline in one of two ways with an applied force shown in the diagram. In each of the trials, the object reaches the top of the incline with speed V. How would the work done by the person on the block compare for the two trials? Assume the same constant non-zero coefficient of kinetic friction between the incline and the object for both trials.
View Solution
