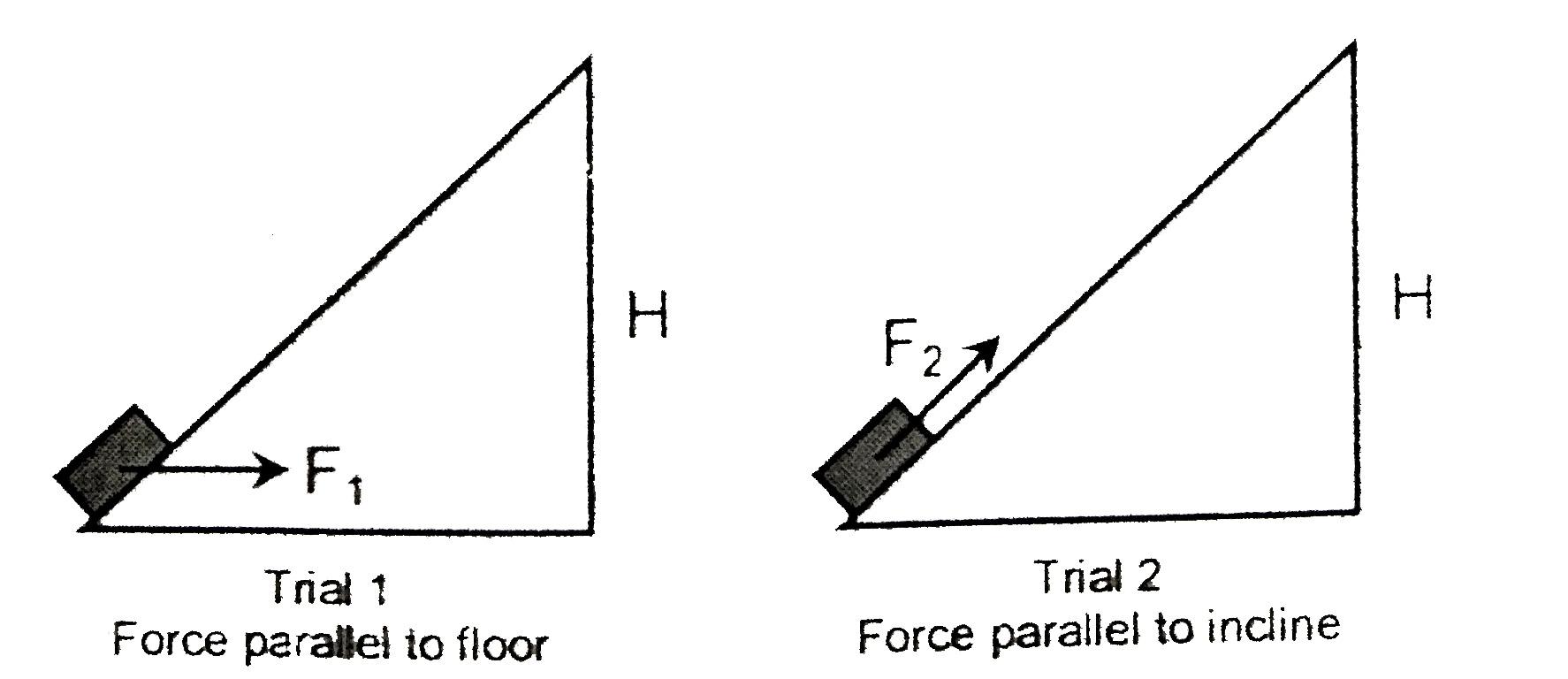
An object of mass M starts from rest at the bottom of a fixed incline of height H. A person decides to push the object up the incline in one of two ways with an applied force shown in the diagram. In each of the trials, the object reaches the top of the incline with speed V. How would the work done by the person on the block compare for the two trials? Assume the same constant non-zero coefficient of kinetic friction between the incline and the object for both trials.
More work would be done in trial 1
More work would be done in trial 2
It is impossible to determine for which trial there would be more work done without knowing the value of the speed V.
It is impossible to determine for which trial there would be more work done without knowing the value of the coefficient of kinetic friction.
The correct Answer is:A
Using work energy theorem, we get ∑W1=∑W2
[Wg+Wfriction]1=[Wg+Wfriction]2
Since |f1|>|f2|⇒[Wext]1>[Wext]2
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
If the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10ms at the bottom of the inclined then work done by the friction force on the block will be
View Solution
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
Am0BmCm2Dm−1A solid sphere starts from rest at the top of an incline of height h and length l, and moves down. The force of friction between the sphere and the incline is F. This is insufficient to prevent slipping. The kinetic energy of the sphere at the bottom of the incline is W.
AThe work done against the force of friction is Fl.BThe heat produced is Fl.CW=mgh-FlDW>(mgh-Fl)
A block of mass m is released from the top of fixed inclined smooth plane. if theta is the angle of inclination then vertical accelertion of block is
View Solution
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.
View SolutionA solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by
View SolutionAn object of mass m is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
View SolutionAn object in projected up the inclined at the angle shown in the figure with an initial velocity of 30ms−1.The distance x up the incline at with the object lands is

View Solution