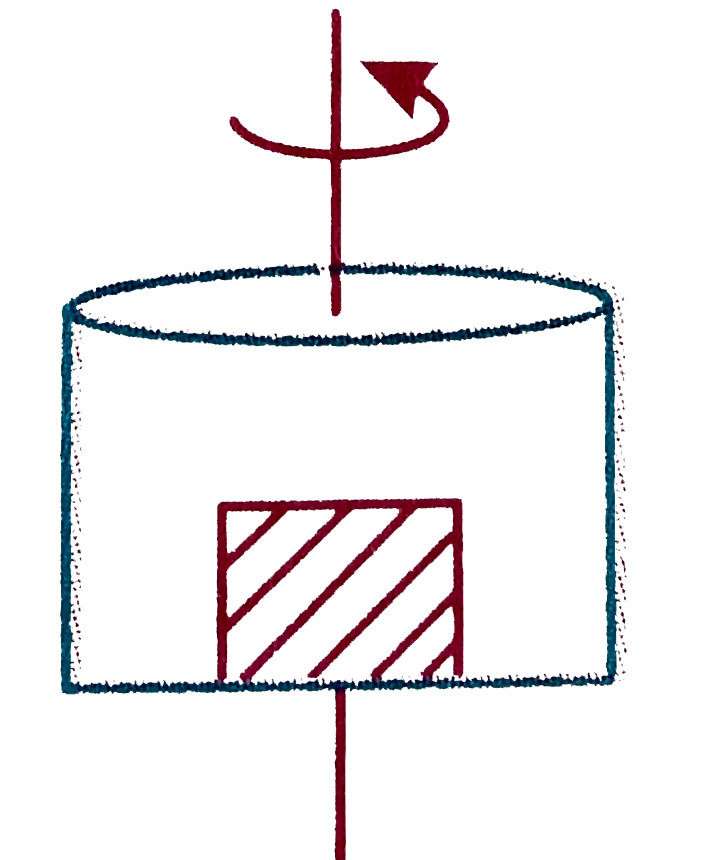
A horizontal platform is rotating with uniform angular velcity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass m is dropped at the centre and is allowed to spread out and finally fall. The angular velocity during this period :
decrease continuously
decreases initially and increases again
remains unaltered
increases continuously
The correct Answer is:B
From law of conservation of angular momentum if no external torque is acting upon a body rotating about an axis, then the angular momentum of the body remains constant that is
J=Iω= constant
Hence, if I decreases , ω increases and vice-versa. Hence liquid is dropped, mass increases hence I increases (I=mr2). So, ω decreases, but as soon as the liquid starts falling ω increases again.
Topper's Solved these Questions
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - General Kinematics
30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - A2ZCHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Chapter Test
29 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
Similar Questions
A horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View Solution
Knowledge Check
A horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -
 A√32ωRBωR2CωRDωR√2
A√32ωRBωR2CωRDωR√2A uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
Aω06Bω05C4ω05D5ω06A smoothh disc is rotating with uniform angular speed ω about a fixed vertical axis passing through its centre and normal to its plane as shown. A small block of mass m is gently placed at the periphery of the disc. Then (pickup the correct alternative or alternatives)
 AIn comparision to ω the angular speed of the disc now increasesBin comparision to ω the angular speed of the disc now decreasesCin comparision to ω the angular speed of the disc now remains sameDthe block will move tangentially and fall of the disc.
AIn comparision to ω the angular speed of the disc now increasesBin comparision to ω the angular speed of the disc now decreasesCin comparision to ω the angular speed of the disc now remains sameDthe block will move tangentially and fall of the disc.
A uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionA particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View SolutionAn ice block is in a trough which is rotating about vertical axis passing through its centre. When ice melts completely, the angular velocity of the system
View SolutionA horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A rig having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View Solution
