A solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity vm/s. If is to climb the inclind surface then v should be :
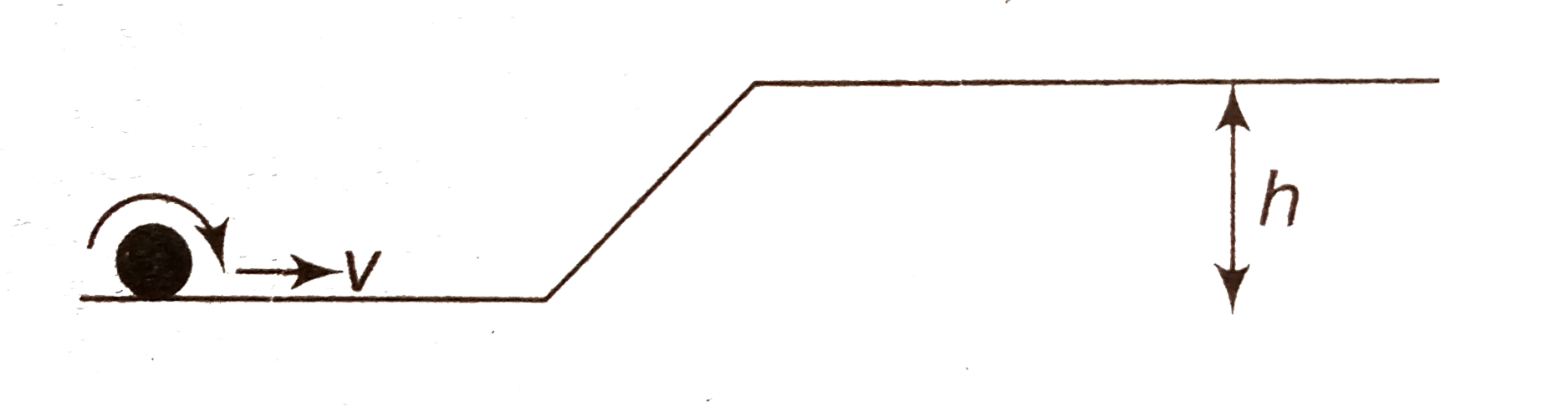
(1)≥√107gh
≥√2gh
2gh
107gh
The correct Answer is:A
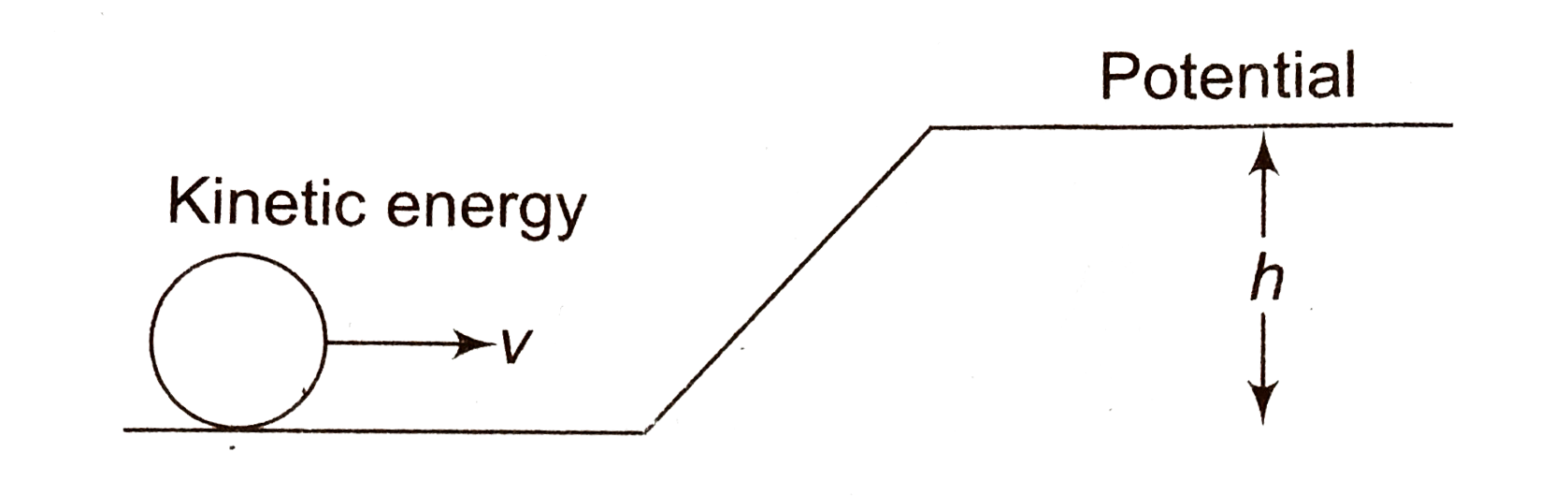
Kinetic energy is converted to potential energy.
From law of conservation of energy, energy can neither be created nor destroyed but it remains conserved. In the given case the sum of kinetic energy of rotation and translation is converted to potential energy.
Also moment of inertia of disc is
I=25Mr2
∴12mv2(Translationalkinetic energy)+12Iω2(Rotationalenergy)=mgh(Potentialenergy)
⇒12mv2+12(25MR2)v2R2=mgh
where v=Rω,ω=anga––rvelocity
⇒710mv2=mgh
⇒v=√107gh
Hence, to climb the inclined surface velocity should be greater than √107gh.
Topper's Solved these Questions
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:General Kinematics
Explore 30 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Chapter Test
Explore 29 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
A solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free and of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be
(Force constant of the spring = 36 N/m)A√14mB√2.8mC√14mD√0.7mA solid sphere is rolled on a rough surface and it is found that sphere stops after some time.
AFriction decreases the linear speedBTorque of friction tries to increase the angular speedCTorque of normal reaction tries to decrease the angular speedDNormal reaction decreases the linear speedTwo men A and B of masses 50kg and 20g respectively are at rest on a frictionless surface as shown in figure. If A pushes B with relative velocity 0.7m/s then find velocity of A just after the push.
_2019_CBT7_E01_018_Q01.png) A0.5m/sB1m/sC5m/sD4m/s
A0.5m/sB1m/sC5m/sD4m/s
A hollow sphere rolls without slipping the on the horizontal surface such that its translational velocity is v. Find that the maximum height attained by it on an inclined surface.

View SolutionA rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
View SolutionA sphere is moving on a smooth surface with linear speed v0 and angular velocity ω0. It finds a rough inclined surface and it starts climbing up:

View SolutionWhen a solid sphere is rolling along level surface the percentage of its total kinetic energy that is translational is
View SolutionA uniform solid sphere of radius r is rolling on a smooth horizontal surface with velocity v and angular velocity ω=(v=ωr). The sphere collides with a sharp edge on the wall as shown in figure. The coefficient of friction between the sphere and the edge μ=1/5. Just after the collision the angular velocity of the sphere becomes equal to zero. The linear velocity of the surface just after the collision is equal to

View Solution


