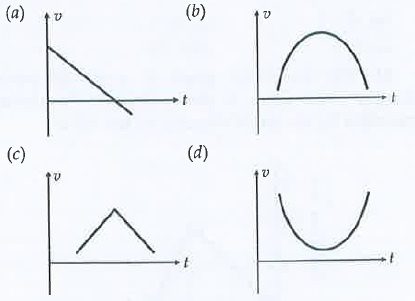
A particle is thrown above, then correct v−t graph will be
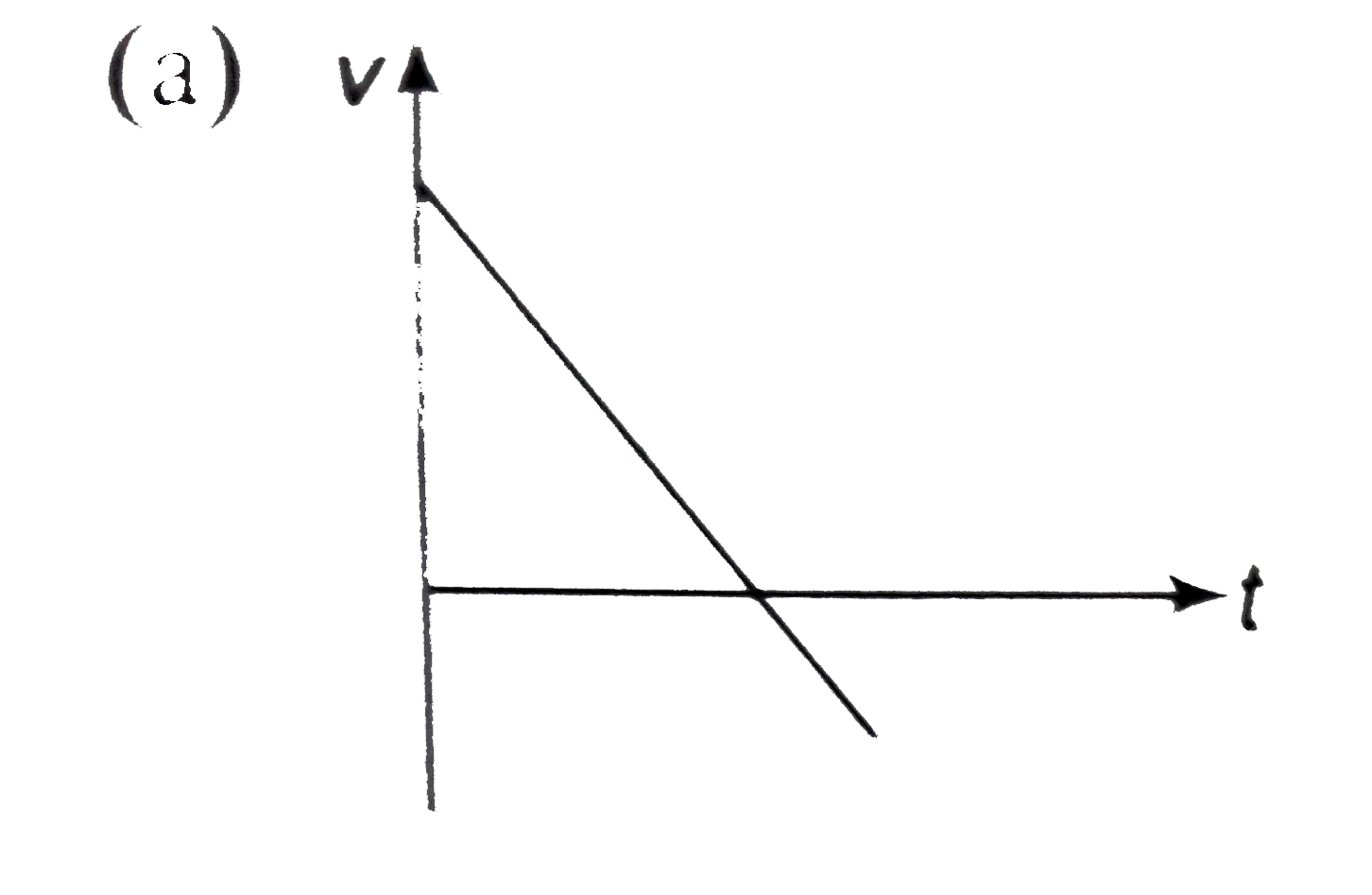


The correct Answer is:A
To solve the problem of determining the correct velocity-time (v-t) graph for a particle thrown upwards, we can follow these steps:
1. Understanding the Motion:
- When a particle is thrown upwards, it initially moves against the force of gravity. As it ascends, its velocity decreases until it reaches a maximum height where the velocity becomes zero.
2. Initial Conditions:
- Let’s denote the initial velocity of the particle as u (which is positive since it is thrown upwards).
- At t=0, the velocity v=u.
3. Velocity Decrease:
- As the particle rises, the acceleration due to gravity (g) acts downwards, causing the velocity to decrease.
- The relationship between initial velocity, final velocity, acceleration, and time can be described by the equation:
v=u−gt
- This equation indicates that the velocity decreases linearly with time until it reaches zero.
4. Maximum Height:
- At the maximum height, the velocity v becomes zero. This occurs at a certain time t=tmax, where:
0=u−gtmax⟹tmax=ug
5. Velocity After Maximum Height:
- After reaching the maximum height, the particle starts to fall back down. The velocity will now be negative (since it is moving in the opposite direction).
- The velocity as it falls can be described by:
v=0+gt(for t>tmax)
- This indicates that the velocity increases in magnitude but remains negative as the particle falls back down.
6. Graph Representation:
- The v-t graph will start at u (positive), decrease linearly to zero at tmax, and then continue to decrease (becoming negative) as the particle falls back down, increasing in magnitude.
7. Conclusion:
- The correct v-t graph will show a linear decrease from u to 0, followed by a linear increase in the negative direction (indicating increasing speed downwards).
Final Answer:
The correct v-t graph for a particle thrown upwards is represented by option A, which shows the described behavior.
- When a particle is thrown upwards, it initially moves against the force of gravity. As it ascends, its velocity decreases until it reaches a maximum height where the velocity becomes zero.
- Let’s denote the initial velocity of the particle as u (which is positive since it is thrown upwards).
- At t=0, the velocity v=u.
- As the particle rises, the acceleration due to gravity (g) acts downwards, causing the velocity to decrease.
- The relationship between initial velocity, final velocity, acceleration, and time can be described by the equation:
v=u−gt
- This equation indicates that the velocity decreases linearly with time until it reaches zero.
- At the maximum height, the velocity v becomes zero. This occurs at a certain time t=tmax, where:
0=u−gtmax⟹tmax=ug
- After reaching the maximum height, the particle starts to fall back down. The velocity will now be negative (since it is moving in the opposite direction).
- The velocity as it falls can be described by:
v=0+gt(for t>tmax)
- This indicates that the velocity increases in magnitude but remains negative as the particle falls back down.
- The v-t graph will start at u (positive), decrease linearly to zero at tmax, and then continue to decrease (becoming negative) as the particle falls back down, increasing in magnitude.
- The correct v-t graph will show a linear decrease from u to 0, followed by a linear increase in the negative direction (indicating increasing speed downwards).
The correct v-t graph for a particle thrown upwards is represented by option A, which shows the described behavior.
Topper's Solved these Questions
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:General Kinematics
Explore 30 Videos
- MOCK TESTBook:A2ZChapter:MOCK TESTExercise:Motion With Constant Acceleration
Explore 15 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:A2ZChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Chapter Test
Explore 29 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
A particle is thrown vertically upwards. The correct graph between its speed (v) and time (t) is given by (neglecting air resistance)
A B
B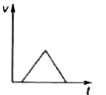 C
C D
D
A particle moves with constant acceleration a in the positive x-axis. At t=0 the particle is at origin is at rest , then correct graph between (velocity)2 and displacement is :
A B
B C
C D
D
The acceleration versus time graph of a particle is shown in the figure. The respective v−t graph of the particle is .
 .A
.A .B
.B .C
.C .D
.D .
.
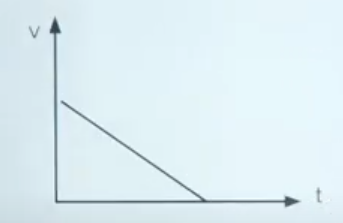
From given v-t graph identify correct a-t graph
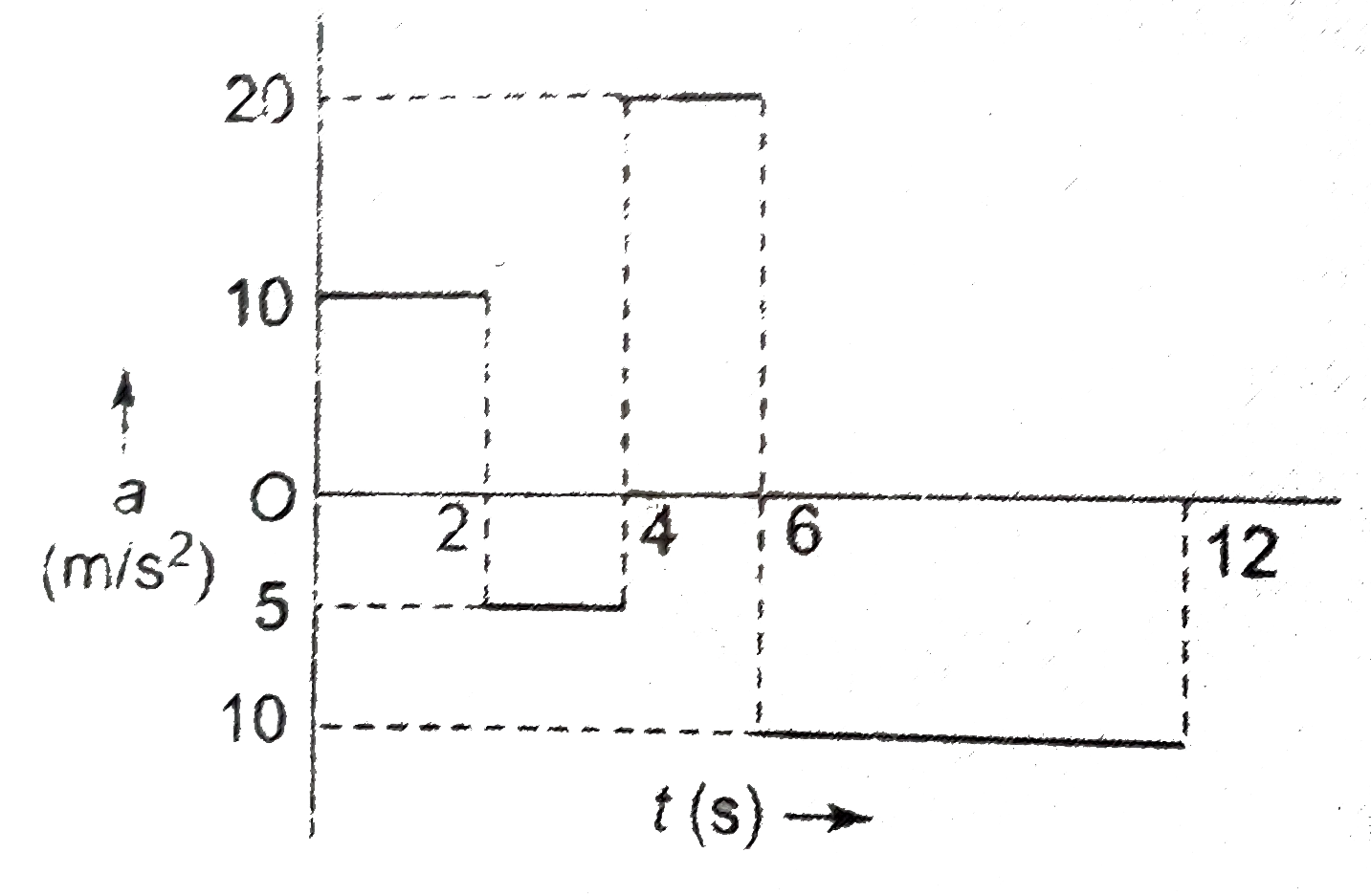
View SolutionA particle is moving along the x-axis. Consider it’s a-t graph. If initial velocity is 10 m//s, sketch the v-t graph and calculate the displacement in the time interval t=0 to 12 s.
View SolutionA particle obeys the following v - t graph as shown. The average velocity over 30 s is

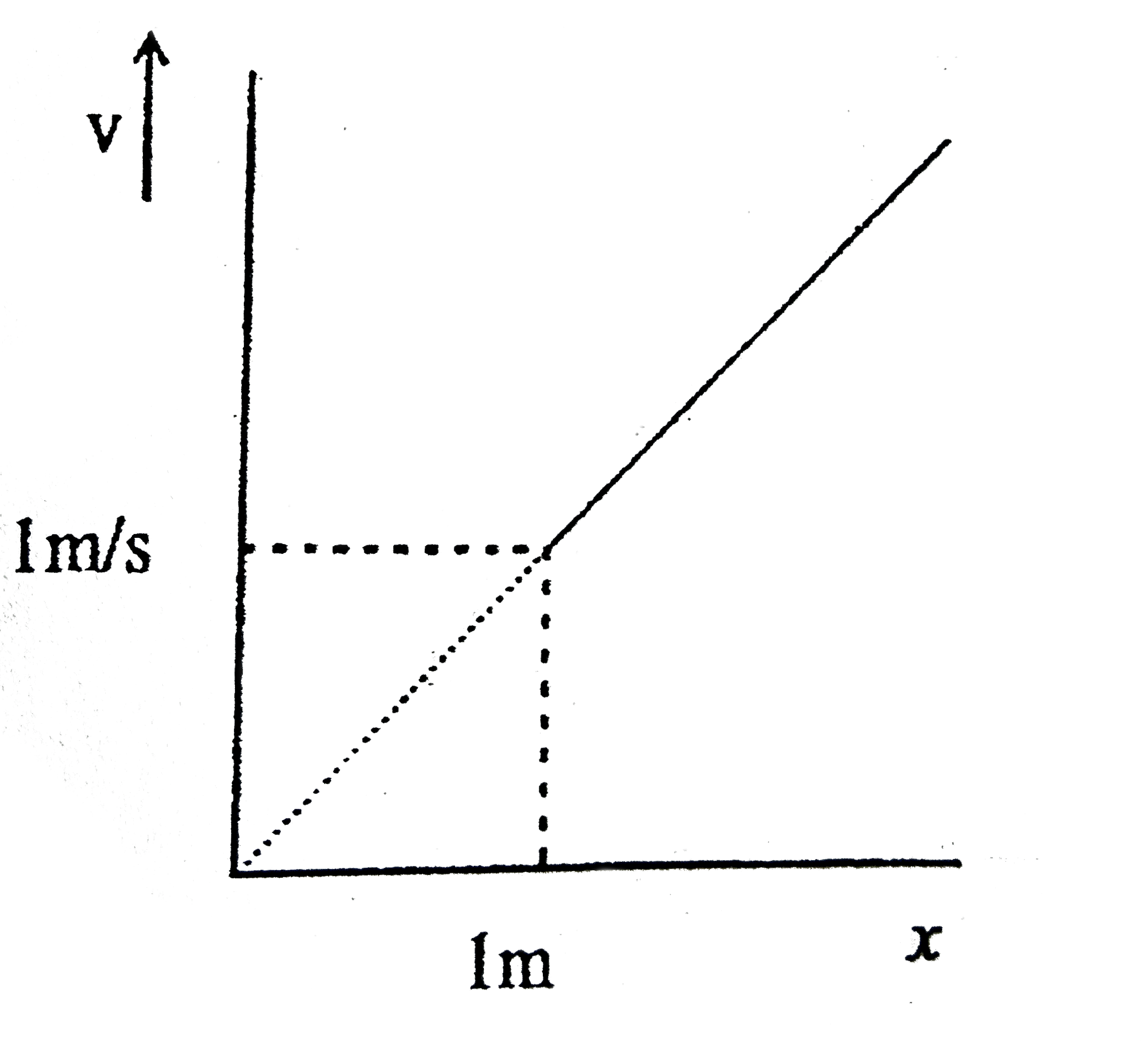
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
View SolutionA particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Which of the following graph may be correct for the motion of particle
View Solution