A U tube pf uniform born of cross sectional area A has been set up vertically with open ends facing up Now mgm of a liquid of density d is poured into it. The column of liquid in this tube will oscillation with a period T such that
T=2π√Mg
T=2π√MAgd
T=2π√MgdA
T=2π√M2Adg
The correct Answer is:D
To find the period of oscillation T of the liquid column in a U-tube, we can follow these steps:
Step 1: Understand the System
We have a U-tube of uniform cross-sectional area A with a liquid of density d poured into one side. When the liquid is displaced by a height y, it creates a restoring force due to the weight of the liquid column.
Step 2: Calculate the Force Acting on the Liquid
The weight of the liquid column that is causing the oscillation can be expressed as:
F=mg
where m is the mass of the liquid. The mass can be expressed in terms of density and volume:
m=d⋅V
The volume V of the liquid in the U-tube can be expressed as:
V=A⋅h
where h is the height of the liquid column.
Step 3: Determine the Displacement
When the liquid is displaced by a height y, the height of the liquid in one side of the U-tube decreases by y and increases by y in the other side. The effective height difference that contributes to the restoring force is 2y.
Step 4: Calculate the Restoring Force
The restoring force F due to the height difference can be calculated as:
F=Weight of the liquid column=Density×Volume×g=d⋅(A⋅2y)⋅g=2Adgy
Step 5: Relate Force to Acceleration
According to Newton's second law, the acceleration a can be expressed as:
F=m⋅a
where m is the mass of the liquid column. The mass m can be expressed as:
m=d⋅(A⋅h)
For small oscillations, we can assume that the total mass of the liquid in the U-tube is M.
Step 6: Write the Equation of Motion
The acceleration a can be expressed as:
a=FM=2AdgyM
This indicates that the acceleration is proportional to the displacement y, which is characteristic of simple harmonic motion (SHM).
Step 7: Determine the Time Period
The time period T of SHM is given by:
T=2π√mk
where k is the effective spring constant. In our case, we can relate it to the restoring force:
k=Fy=2AdgM
Thus, the time period can be expressed as:
T=2π√M2Adg
Final Expression
The final expression for the period of oscillation T is:
T=2π√M2Adg
We have a U-tube of uniform cross-sectional area A with a liquid of density d poured into one side. When the liquid is displaced by a height y, it creates a restoring force due to the weight of the liquid column.
The weight of the liquid column that is causing the oscillation can be expressed as:
F=mg
where m is the mass of the liquid. The mass can be expressed in terms of density and volume:
m=d⋅V
The volume V of the liquid in the U-tube can be expressed as:
V=A⋅h
where h is the height of the liquid column.
When the liquid is displaced by a height y, the height of the liquid in one side of the U-tube decreases by y and increases by y in the other side. The effective height difference that contributes to the restoring force is 2y.
The restoring force F due to the height difference can be calculated as:
F=Weight of the liquid column=Density×Volume×g=d⋅(A⋅2y)⋅g=2Adgy
According to Newton's second law, the acceleration a can be expressed as:
F=m⋅a
where m is the mass of the liquid column. The mass m can be expressed as:
m=d⋅(A⋅h)
For small oscillations, we can assume that the total mass of the liquid in the U-tube is M.
The acceleration a can be expressed as:
a=FM=2AdgyM
This indicates that the acceleration is proportional to the displacement y, which is characteristic of simple harmonic motion (SHM).
The time period T of SHM is given by:
T=2π√mk
where k is the effective spring constant. In our case, we can relate it to the restoring force:
k=Fy=2AdgM
Thus, the time period can be expressed as:
T=2π√M2Adg
The final expression for the period of oscillation T is:
T=2π√M2Adg
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Superposition Of Shm And Compound Pendulum
Explore 19 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Problems Based On Mixed Concepts
Explore 24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Spring Particle System
Explore 24 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Chapter Test
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
Similar Questions
A U-tube of uniform cross-sectional area and open to the atmosphere is partially filled with mercury. Water is then poured into both arms. If the equilibrium configuration of the tube is as shown in figure with h2=1.0cm, determine the value of h1
 .
.
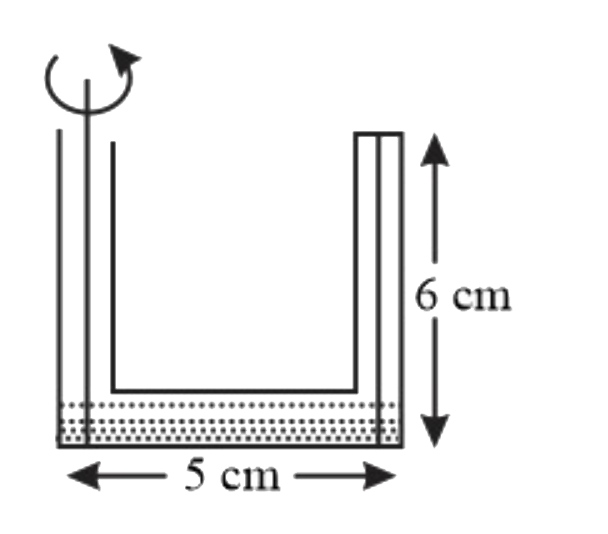
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View Solution
Knowledge Check
A V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillation of liquid.
 Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of these
Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of theseA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is
 AF=0BρAv2C2ρAv2D12ρAv2
AF=0BρAv2C2ρAv2D12ρAv2Fig, shows a U-tube of uniform cross-sectional area A accelerated with acceleration a as shown. If d is the seperation between the limbs. Then the difference in the levels of the liquid in the U−tube is
 AadgBgadCadgDad+g
AadgBgadCadgDad+g
Length of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View SolutionA test tube of length l and area of cross-section A has some iron fillings of mass M. The test tube floats normally in a liquid of density ρ with length x dipped in the liquid. A distribuing force makes the tube oscillate in the liquid. The time period of osciallation is given by (neglect the mass of the test tube)
View SolutionA U-tube having horizontal arm of length 20 cm, has uniform cross-sectional area=1cm2, It is filled with water of volume 60 cc. What volume of a liquid of density 4g/ should be poured from one side into the U-tube so that no water is left in the horizontal arm of the tube?
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
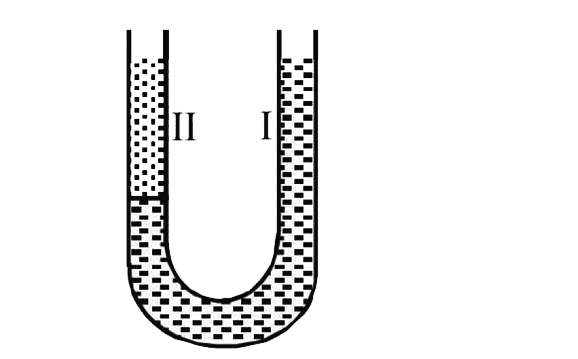
View SolutionA U-tube of uniform cross section (see figure) is partially filled with a liquid I. Another liquid II which does not mix with liquid I is poured into one side. It is found that the liquid levels of the two sides of the tube are the same, while the level of liquid I has risen by 2cm. If the specific gravity of liquid I is 1.1, the specific gravity of liquid II must be
View Solution

