A partical of mass m is projected with velocity u at an angle α with horizontal. During the period when the partical desconds from highest point to the position where
its velocity vector makes an angle α2 with horizontal. Wiork done by gravity force is
12μ2tan2α
12μ2cos2(α)2
12μ2cos2αtan2(α)2
12μ2cos2(α)2sin2α
The correct Answer is:D
Horizontal component of velocity i.e., ucosα remains unchanged. At highest point vertical component of velocity is zero . Let vy be the vertical component of velocity at the desired instant.
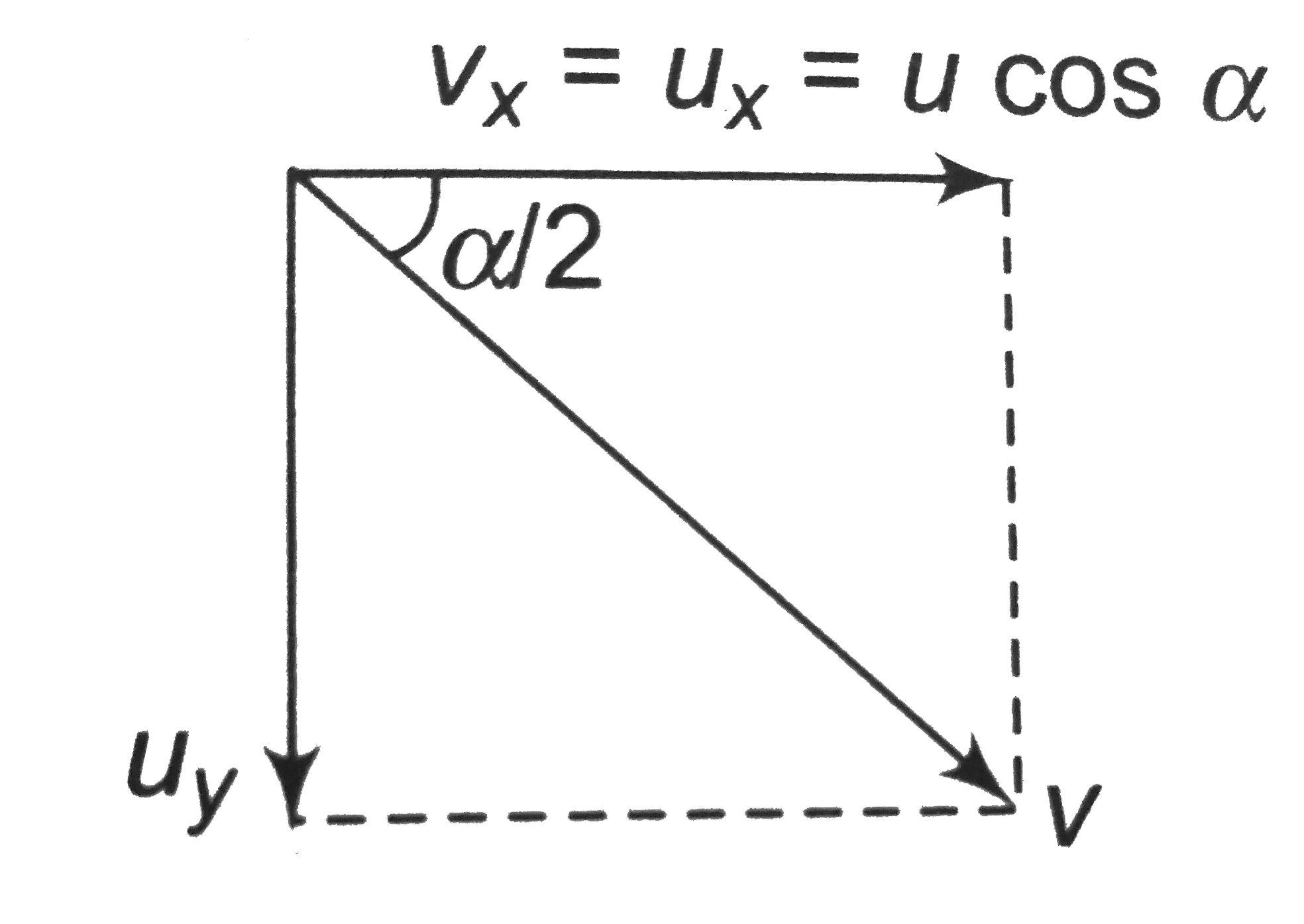
vyvx=tan.α2
vy=vxtan.α2=ucosαtan.α2
Now increase in kinetic energy = work done by gravity
∴ The desired work done W=12mv2y
=12μ2cos2αtan2.α2.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - NEET Questions
49 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
A particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
Amu3sin2θcosθ3gB3mu3sin2θcosθ3gCmu3sin2θcosθ2gD2mu3sinθcos2θ3gA particle of mass m is projected form ground with velocity u making angle θ with the vertical. The de Broglie wavelength of the particle at the highest point is
A∞BhmusinθChmucosθDhmuA particle is projected with initial velocity u making an angle α with the horizontal, its time of flight will be given by
A2usinαgB2u2sinαgCusinαgDu2sinαg
A particle is projected with velocity u at angle θ with horizontal. Find the time when velocity vector is perpendicular to initial velocity vector.
View SolutionA particle of mass m is projected with velocity v at an angle θ with the horizontal. Find its angular momentum about the point of projection when it is at the highest point of its trajectory.
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View SolutionA particle of mass 'm' is projected from ground with velocity u making angle θ with the vertical. The de-Broglie wave length of the particle at the highest point is:
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View Solution
