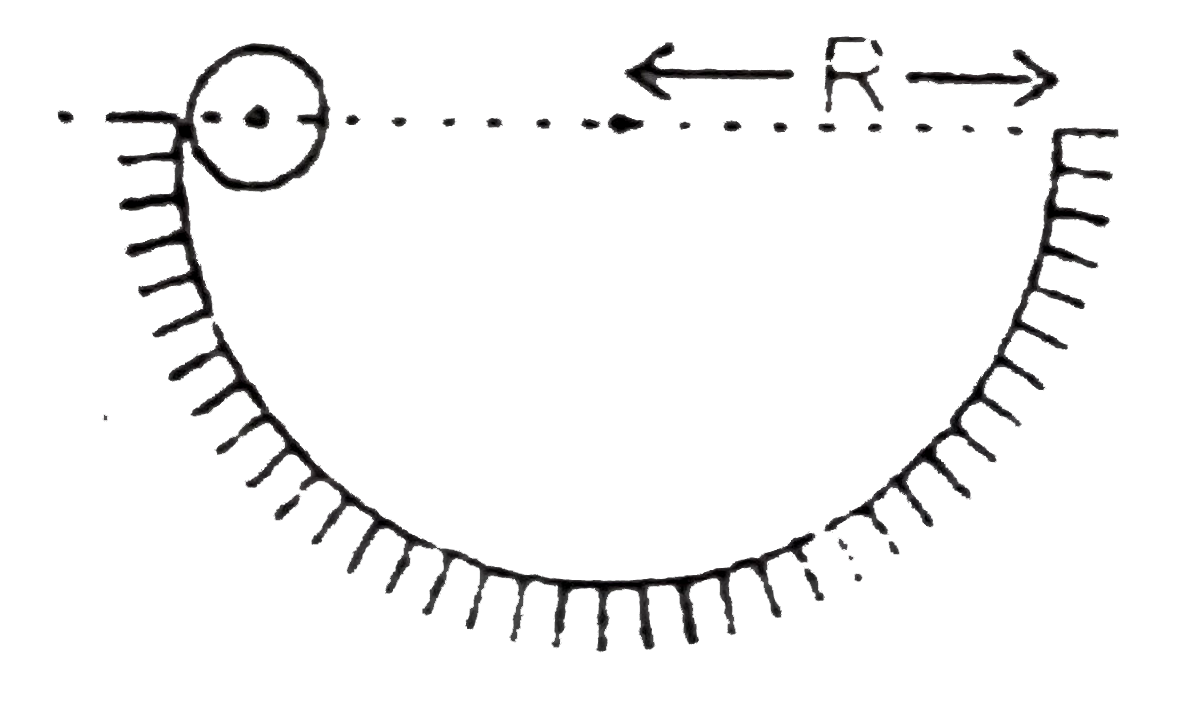
In the figure shown, there is a smooth tube of radius R, fixed in the vertical plane. A ball B of mass m is released from the top of the tube. B slides down due to gravity and compresses the spring is fixed and end A is free., Initially, line OA makes an angle 60∘ with OC and finally it makes an angle of 30∘ after compression. Find the spring constant of the spring.

12mg(2+√3)π2R
36mg(2+√3)π2R
18mgπ2R
None of these
The correct Answer is:D
By energy conservation
mgR(1+cos30∘)=12k(πR6)2
⇒k=36mg(2+√3)π2R
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - NEET Questions
49 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
In the figure shown there is a smooth tube of radius 'R' fixed in the vertical plane A ball 'B' of mass 'm'is released from the top of the tube B slides down due to gravity and compresses the spring the end 'C' of the spring is fixed and the end A is free Initially the line OA makes an angle of 60∘ with OC and finally it makes an angle of 30∘ after compression find the spring constant of the spring
 A12mg(2+√3)π2RB36mg(2+√3)π2RC18mgπ2RDnone of these
A12mg(2+√3)π2RB36mg(2+√3)π2RC18mgπ2RDnone of theseIn the figure shown, a small ball of mass 'm' can move witgout sliding in a fixed semicircular track of radius R in vertical planet. It is released from the top. The resultant force on the ball at the lowest of the track is
 A10mg7B17mg7C3mg7Dzero
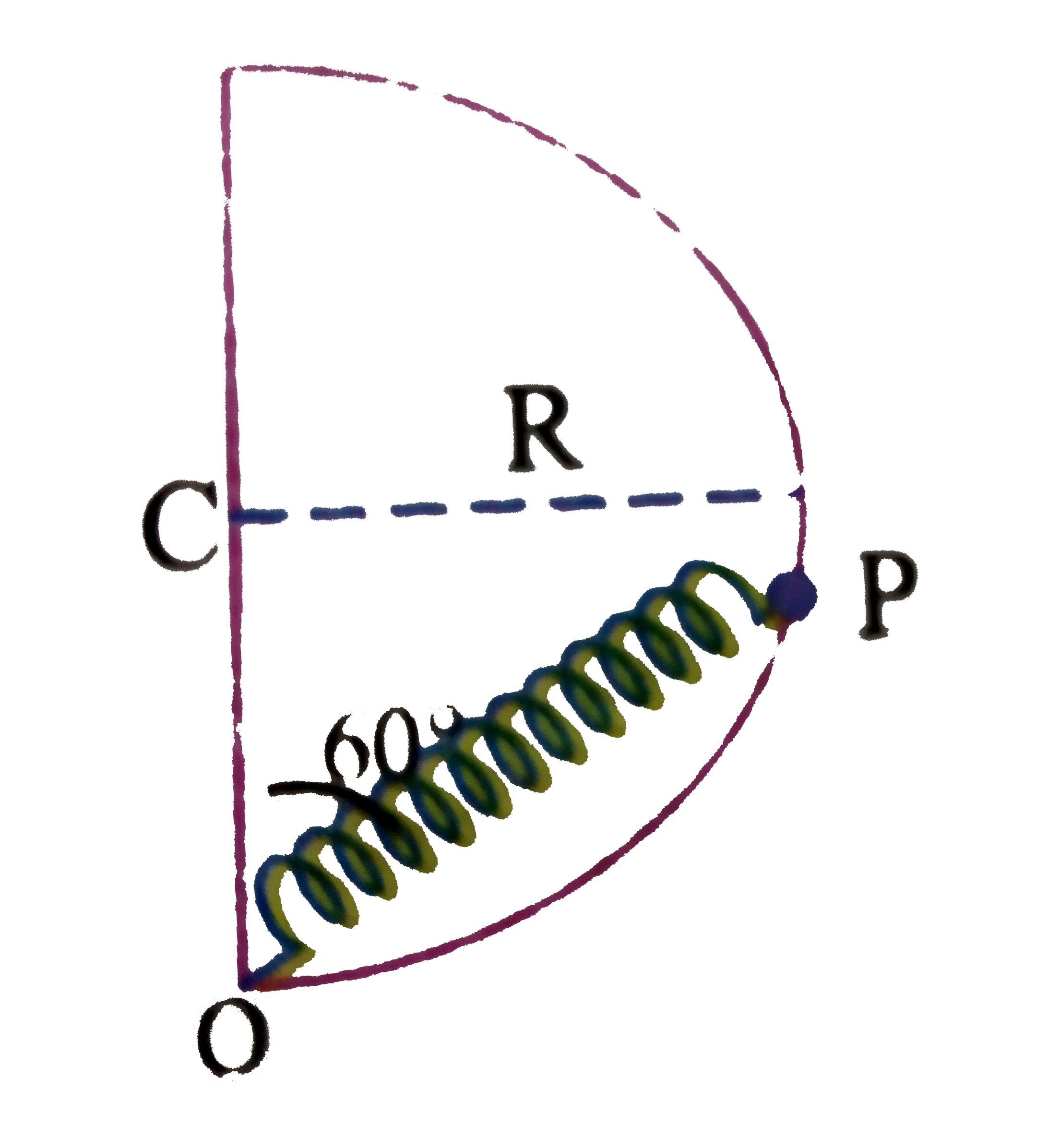
A10mg7B17mg7C3mg7DzeroA smooth semicircular wire track of radius R if fixed in a vertical plane. One end of massless spring of netural length 3R4 is attached to the lowest point O of the wire track. A small ring of mass m which can slide on the track is attched to the other end of the spring. the ring is held stationary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant is K=mgR. considering the instance when the ring is released, the free body diagram of the ring, when aT is tengential acceleration, F is restoring force and N is normal reaction is
 A
A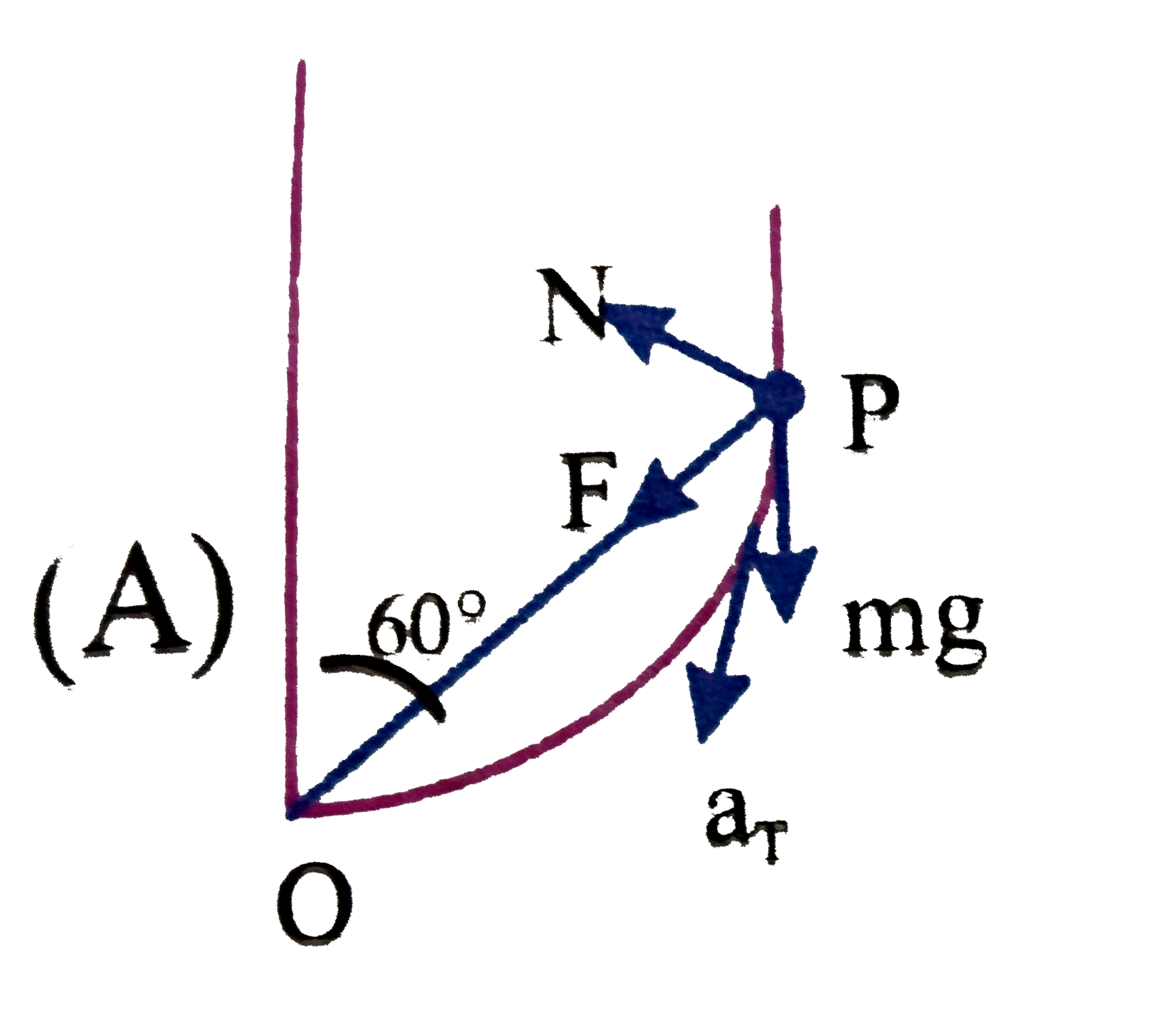 B
B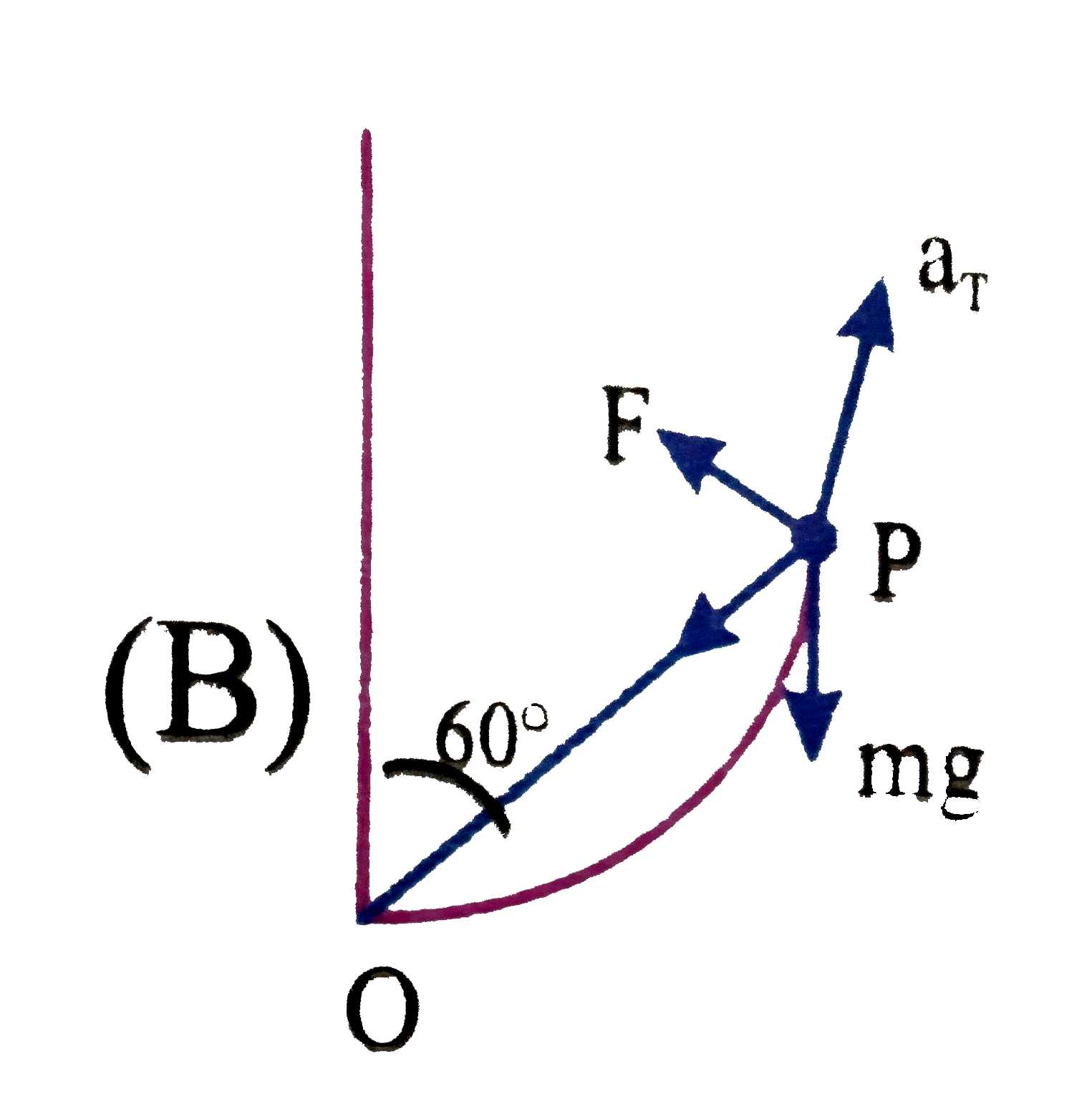 C
C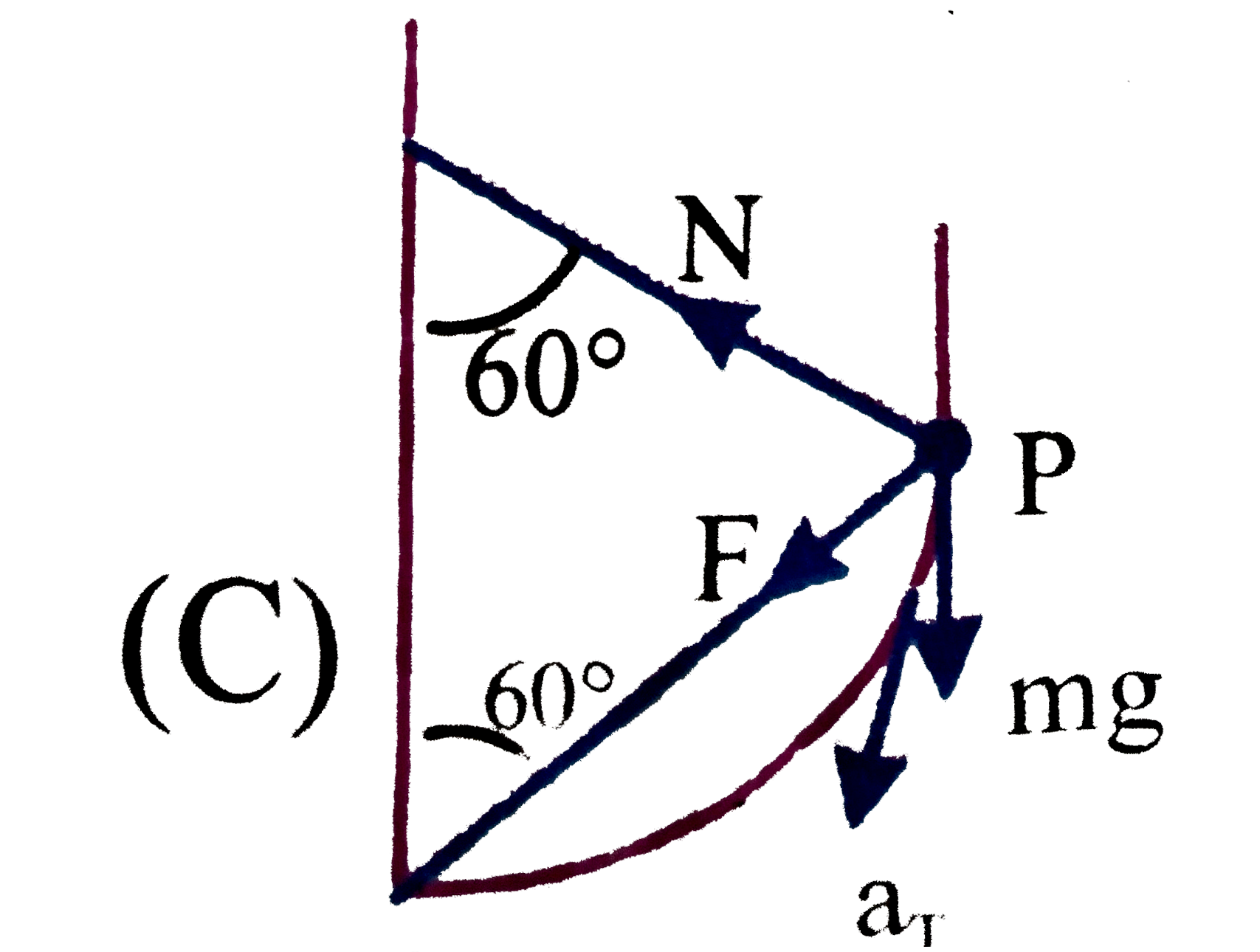 D
D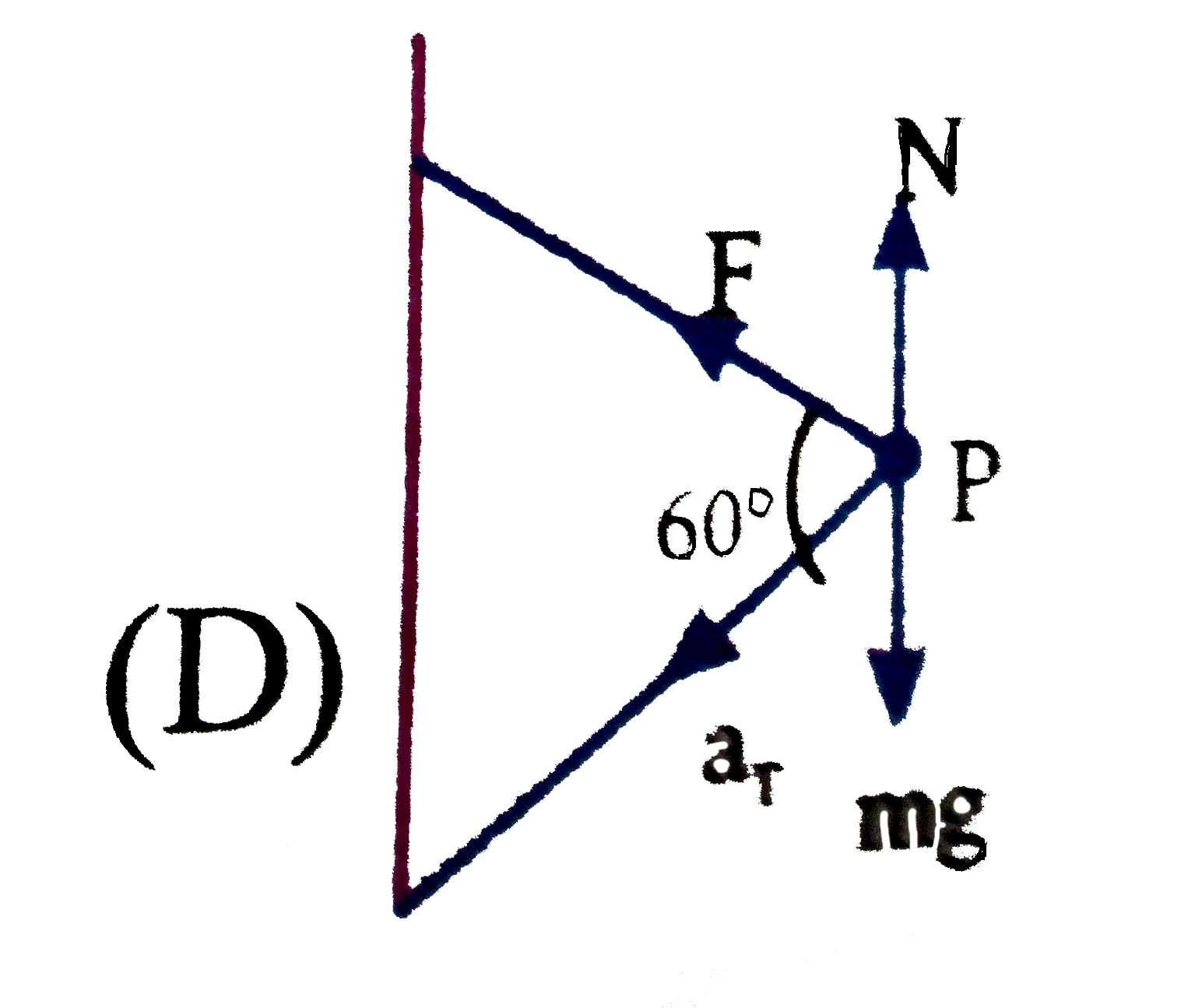
In an ideal pulley particle system, mass m2 is connected with a vertical spring of stiffness k. If mass m2 is released from rest, when the spring is underformed, find the maximum compression of the spring.

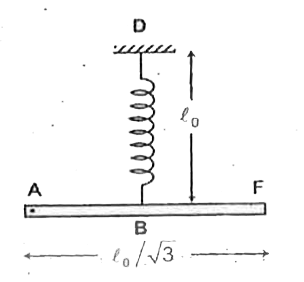
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R/4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant K=mg/R. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

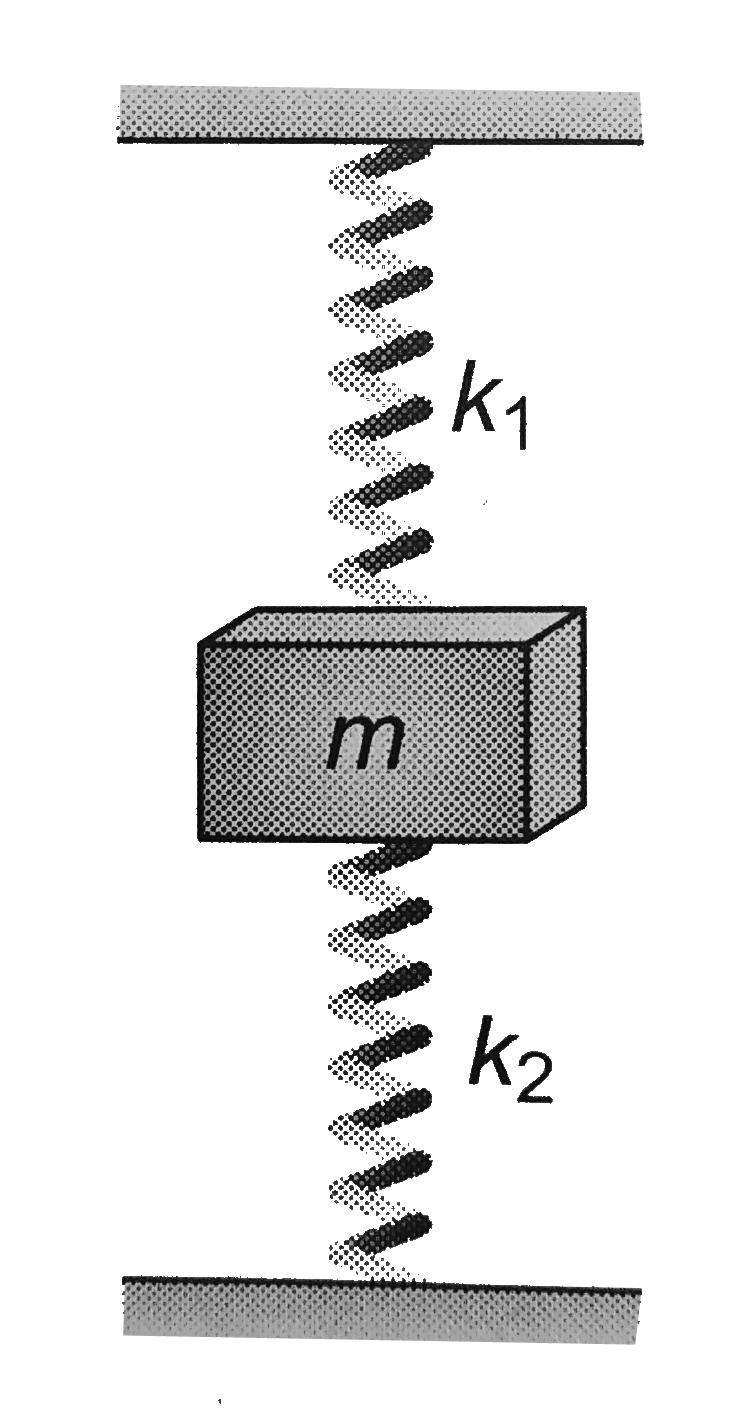
View SolutionIn the figure shown a block of masss m is atteched at ends of two spring The other ends of the spring are fixed The mass m is released in the vertical plane when the spring are released The velocity of the block is maximum when
View Solution

