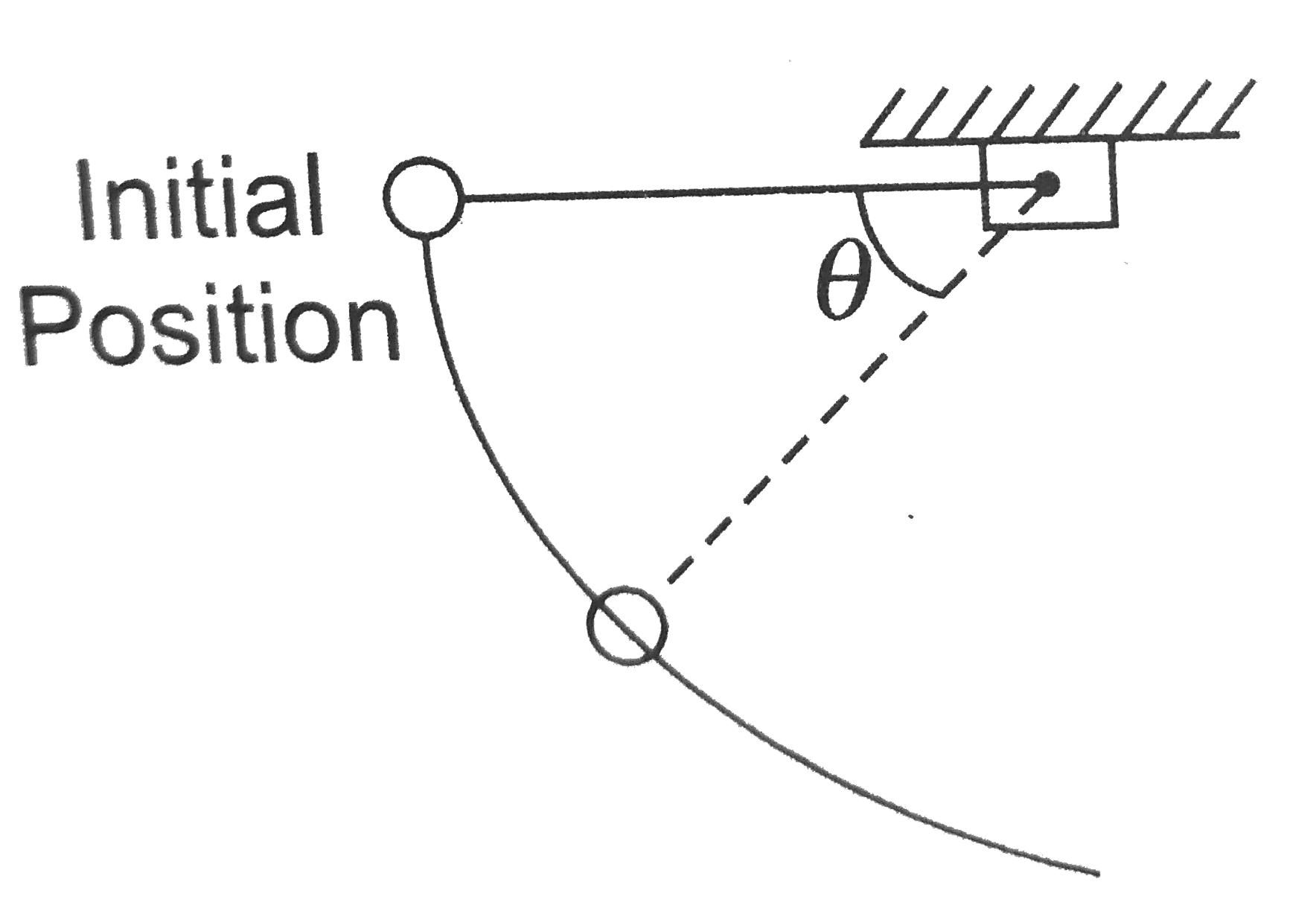
The given figure shows a small mass connected to a string which is atteched to a string , which is attached to a vertical post. If the mass is released from rest when the string is horizontal as shown the magnitude of the total acceleration of the mass as friction of the angle θ is
2gsinθ
2gcosθ
g√3cos2θ+1
g√3sin2θ+1
The correct Answer is:C
From conservation of energy ΔK+ΔU=0
mgh=12mv2mglsinθ=12mv2
⇒aC=2gsinθ=v2l = radius acceleration
gcosθ=at = tangential acceleration
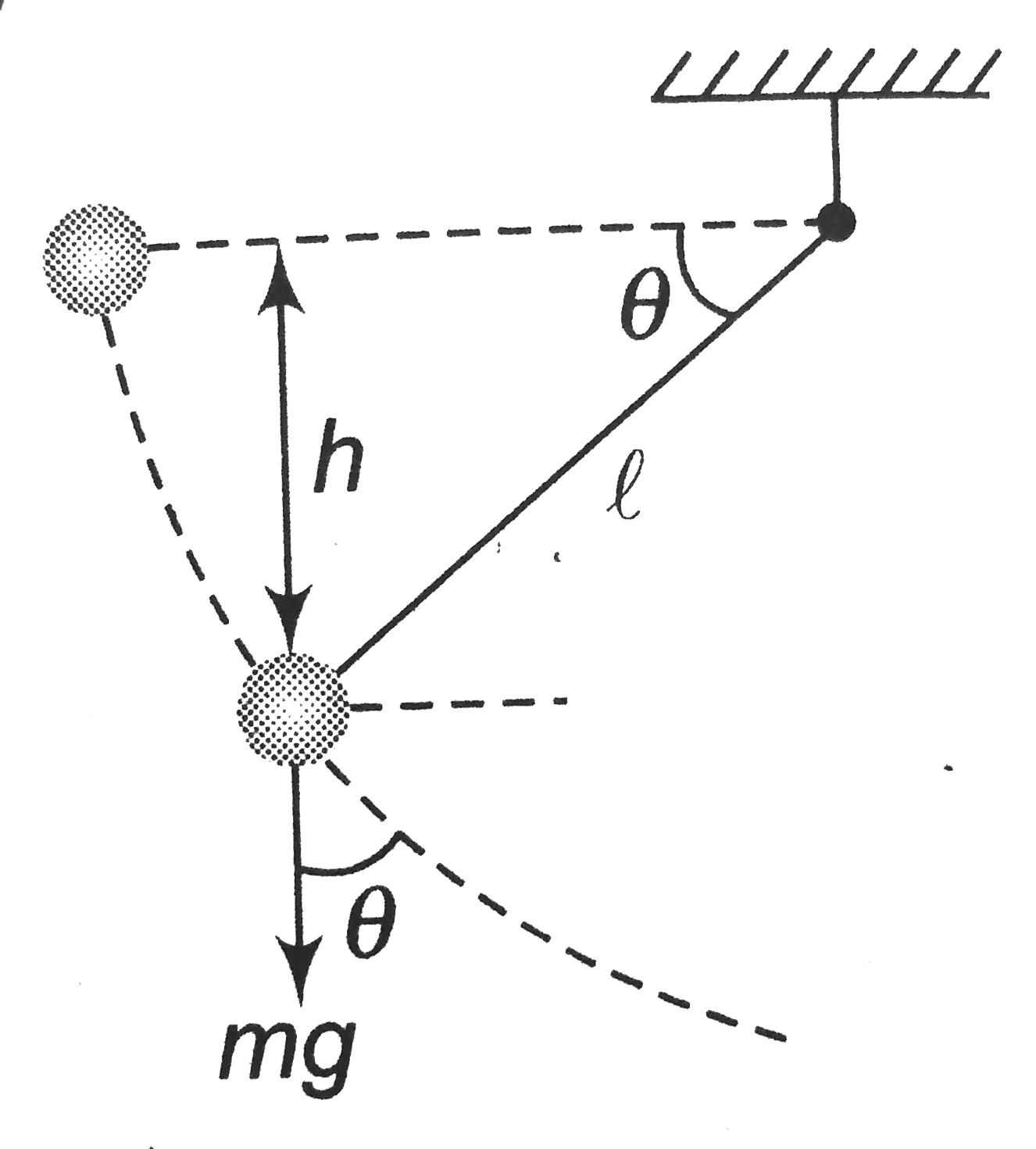
Total acceleration
a=√a2c+a2t=g√cos2θ+(2sinθ)2
=g√(1−sin2θ)+4sin2θ=g√1+3sin2θ.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Assertion Reasoning
Explore 17 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:NEET Questions
Explore 49 Videos
- WORK, ENERGY, POWER AND COLLISIONBook:A2ZChapter:WORK, ENERGY, POWER AND COLLISIONExercise:Collision
Explore 31 Videos
- WAVES AND ACOUSTICSBook:A2ZChapter:WAVES AND ACOUSTICSExercise:Chapter Test
Explore 30 Videos
Similar Questions
Figure below shows a small mass connected to a string, which is attached to a vertical post. If the ball is released when the string is horizontal as shown, the magnitude of the total acceleration (including radial and tangential) of the mass as a function of the angle Θis

View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View Solution
Knowledge Check
In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
Aθ=cos−1(1/3)Bθ=60∘Cθ=cos−1(2/3)Dθ=0A bob of mass m attached with a string of length l tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass m gently stuck to it. Find the maximum angle from the vertical to which it rotates.
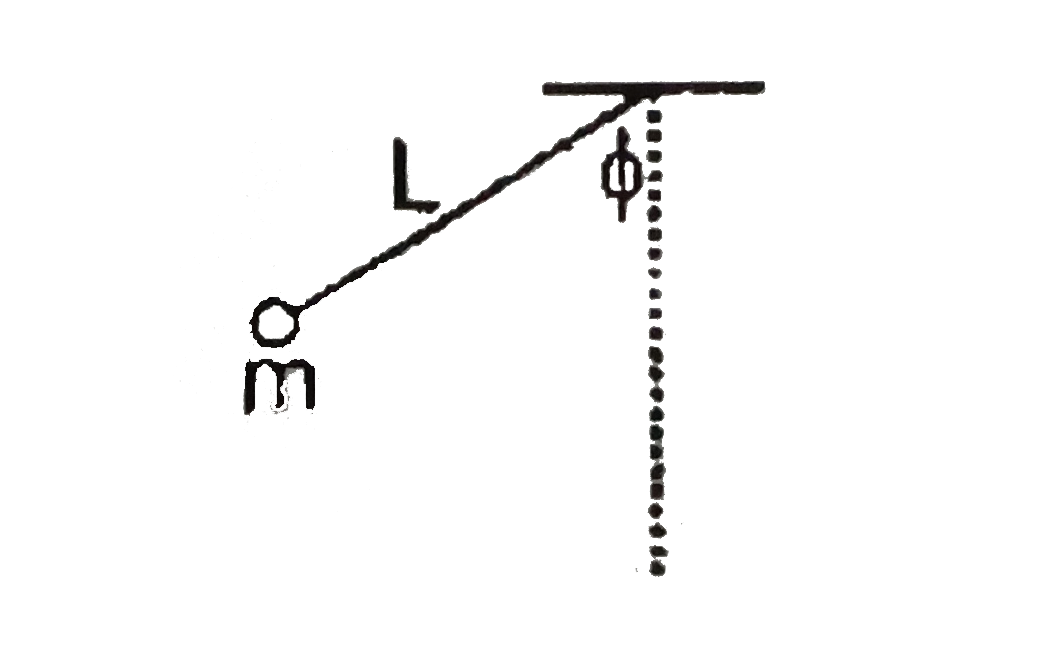
A(a) cos−1(23)B(b) cos−1(34)C(c) cos−1(14)D(d) 60∘A pendulum is made by attaching a ball at the end of a string (the other end of the string is attached to the ceiling). The ball is released from rest at the position shown at some angle ϕ. Which of the following vectors may represent the impulse delivered by the string to the ball from the time it is released unitl the ball is at the bottom of the swing when string becomes vertical
 A
A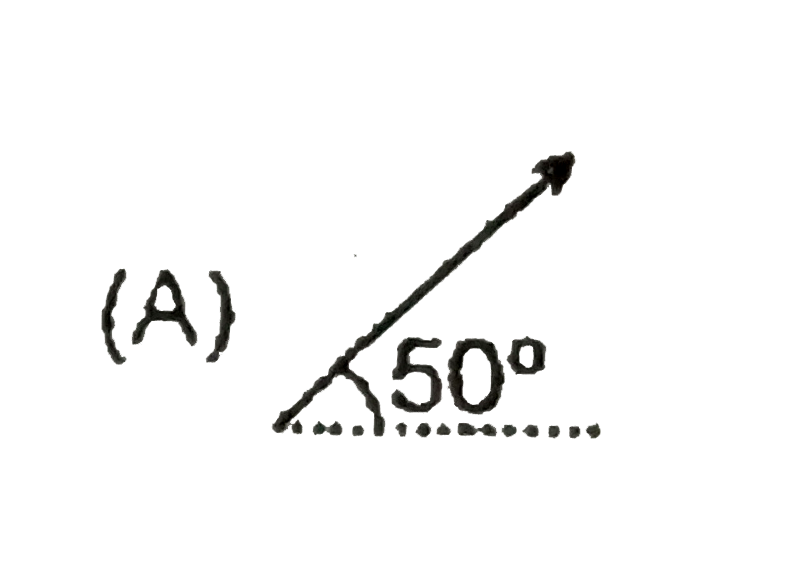 B
B C
C D
D
A ball of mass 1.00 kg is attached to a loose string fixed to a ceiling. The ball is released from rest and falls 2.00 m, where the string suddenly stops it. Find the impulse on it from the string.
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
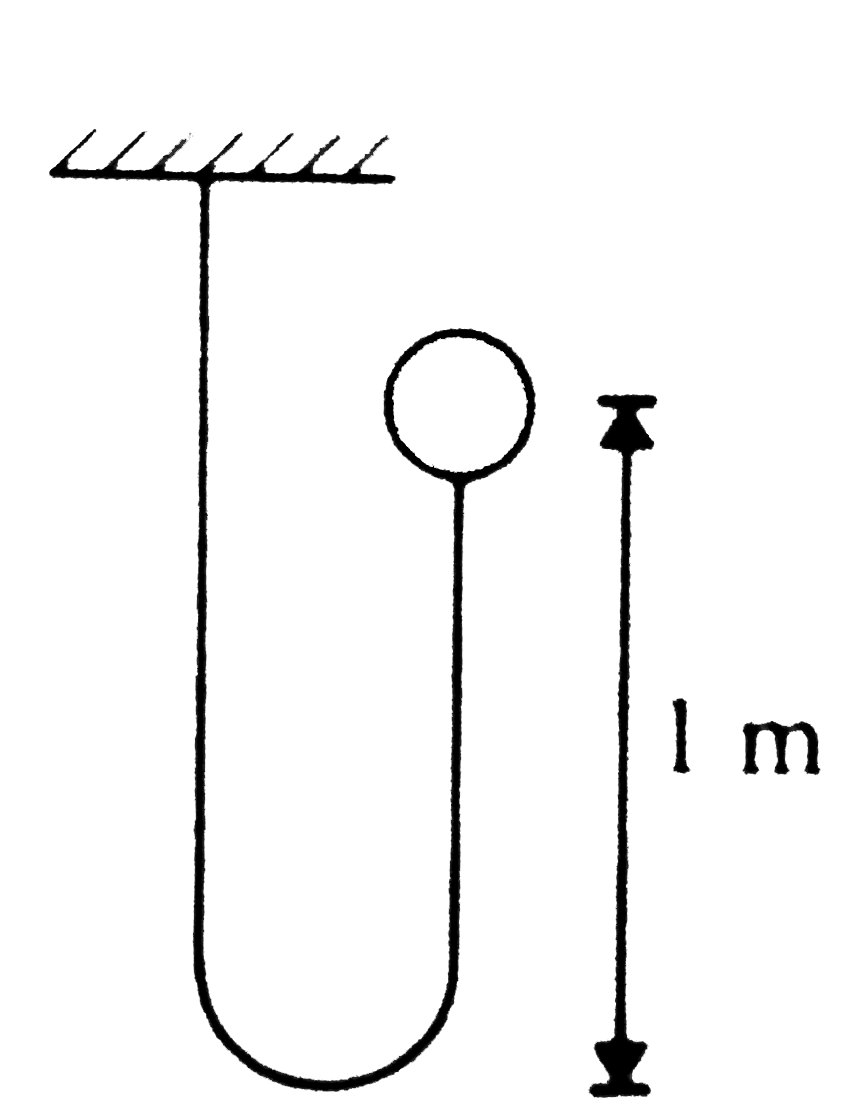
View SolutionA mass attached to one end of a string crosses top - most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be
(where, g=gravitational acceleration)
View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
View SolutionTwo masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
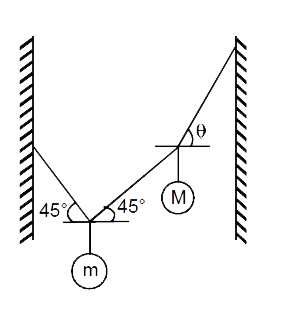
View Solution

