Initially the spring is un deformed. Now the force F is applied to B as shown in the figure. When the displacement of B w.r.t. A is x towards right in some time then relative acceleration of B w.r.t. A at that moment is:

A
F2m
B
F−kxm
C
F−2kxm
D
none of these
Video Solution
Text Solution
The correct Answer is:C
F−kx=mb and kx=ma
Hence m(b−a)h=F−2kx . 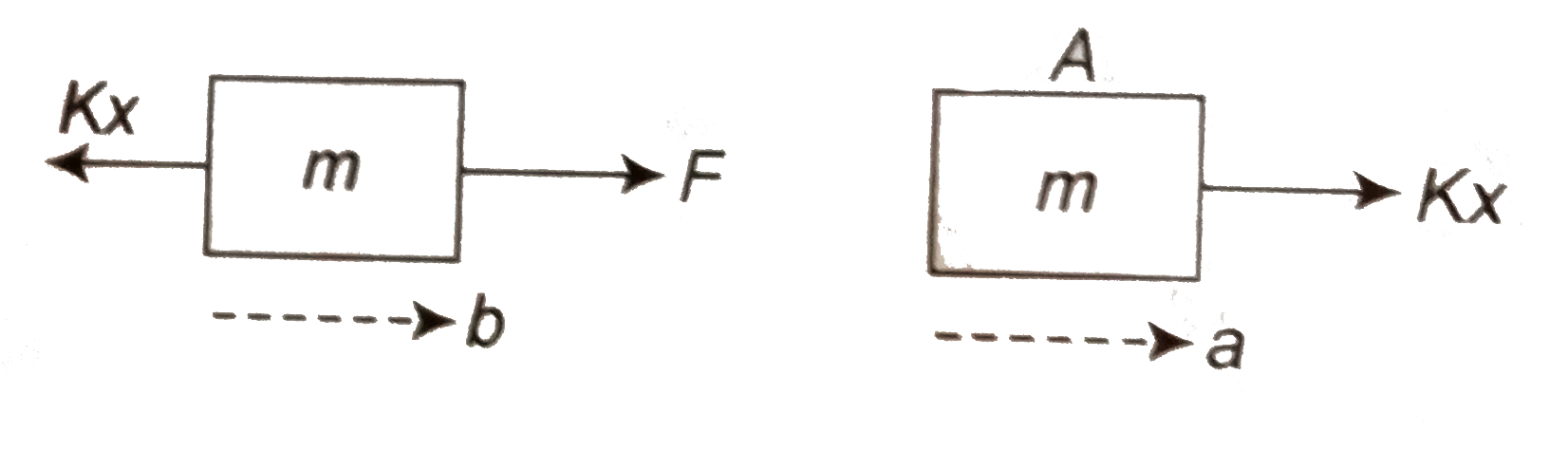
|
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Assertion Reasoning
Explore 14 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:NEET Questions
Explore 38 Videos
- NEWTONS LAWS OF MOTIONBook:A2ZChapter:NEWTONS LAWS OF MOTIONExercise:Dynamics Of Circular Motion
Explore 31 Videos
- MOTION IN TWO DIMENSIONBook:A2ZChapter:MOTION IN TWO DIMENSIONExercise:Chapter Test
Explore 29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBook:A2ZChapter:OSCILLATION AND SIMPLE HARMONIC MOTIONExercise:Chapter Test
Explore 29 Videos
Similar Questions
Knowledge Check
Two particles P and Q are moving as shown in the figure. At this moment of time the angular speed of P w.r.t. Q is
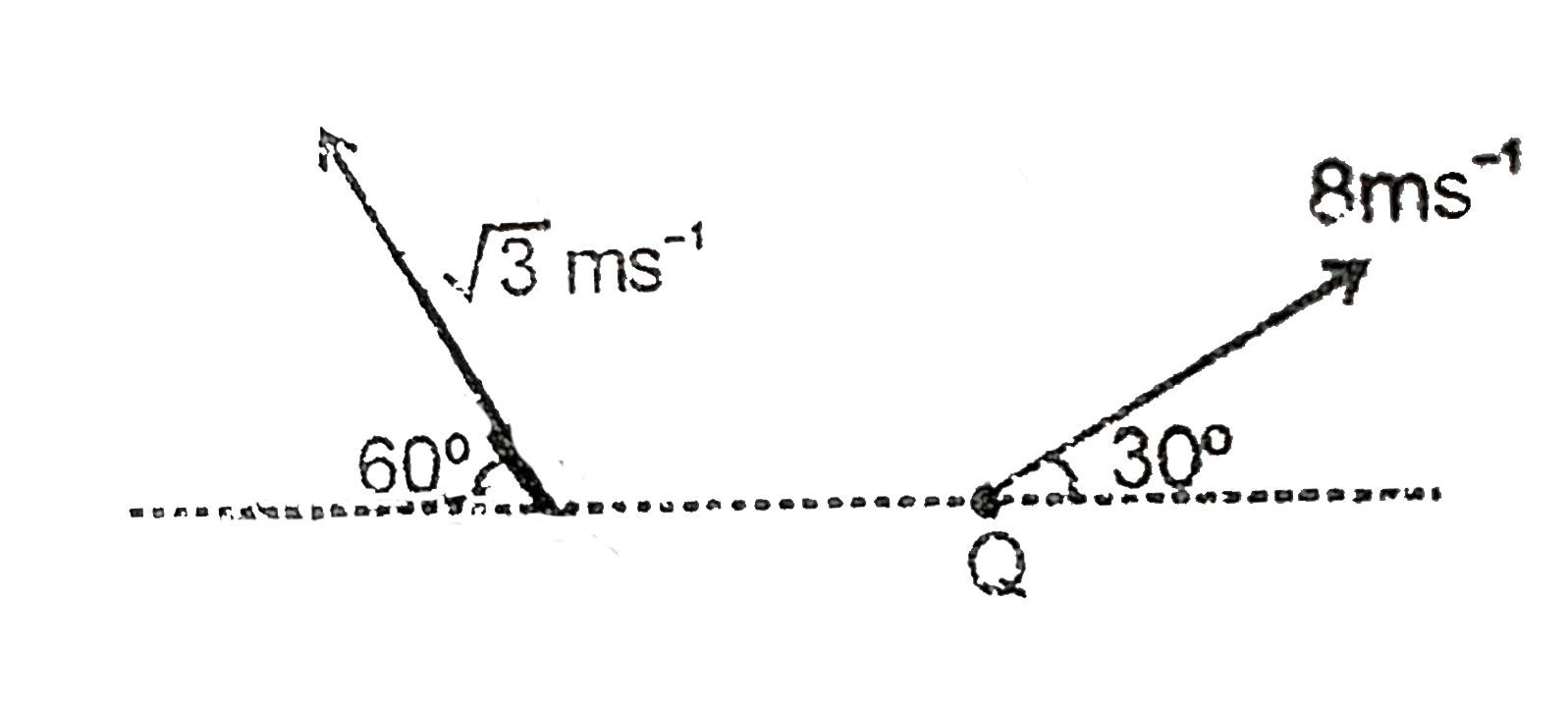 A5 rads−1B4 rads−1C2 rads−1D1 rads−1
A5 rads−1B4 rads−1C2 rads−1D1 rads−1If dispolacement x at time t is x=acosωt−bsinωt, where ω is a constant, then: acceleration=
Aω2xBωxC−ωxD−ω2xA point is placed in front of thick plane mirror as shown in figure. Find the location of final image w.r.t. object.
 A15/2cmB15cmC40/3cmD80/3cm
A15/2cmB15cmC40/3cmD80/3cm
Find the acceleration of block B as shown in fig. (a) and (b) relative to block A and relative to ground if block A is moving toward right with acceleration a.

View SolutionCalculate the relative acceleration of A w.r.t. B if B is moving with acceleration a0 towards right.

View SolutionIf block A is moving with an acceleration of 5ms−2, the acceleration of B w.r.t. ground is

View SolutionThe displacement of a particle varies with time according to the relation y=asinωt+bcosωt.
View SolutionIn the above question, the order w.r.t. B is:
View Solution