The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
The initial velocity of the particle is zero
the initial velocity of the particle is 2.5ms.
The accelration of the particle is 2.5ms2.
The acceleration of the particle is 50ms2.
The correct Answer is:A, D
Given v=10√x
Putting x=0 gives v=0, so initial velocity of the particle is zero.
a=dvdt=102√xdxdt
⇒a=5√xv=5√x10√x=50ms2
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type
491 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Fill in the blanks type
26 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
The velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.
View Solution
Knowledge Check
The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
A12.5ms−2B7.5ms−2C5ms−2D2.5ms−2A particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as v=p√x. The displacement of the particle varies with time as (where, p is constant)
At3Bt2CtDt1/2vx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
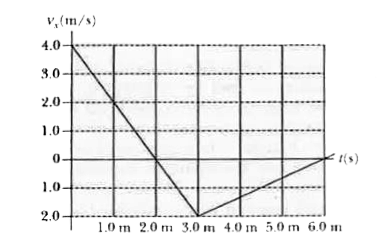 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m
The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionThe velocity of a particle moving in the positive direction of x-axis varies as v=α√x where α is positive constant. Assuming that at the moment t=0, the particle was located at x=0, find (i) the time dependance of the velocity and the acceleration of the particle and (ii) the mean velocity of the particle averaged over the time that the particle takes to cover first s meters of the path.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionVelocity of particle moving along positive x-direction is v=(40−10t)m/s. Here,t is in seconds. At time t=0, tha x coordinate of particle is zero. Find the time when the particle is at a distance of 60 m from origin.
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
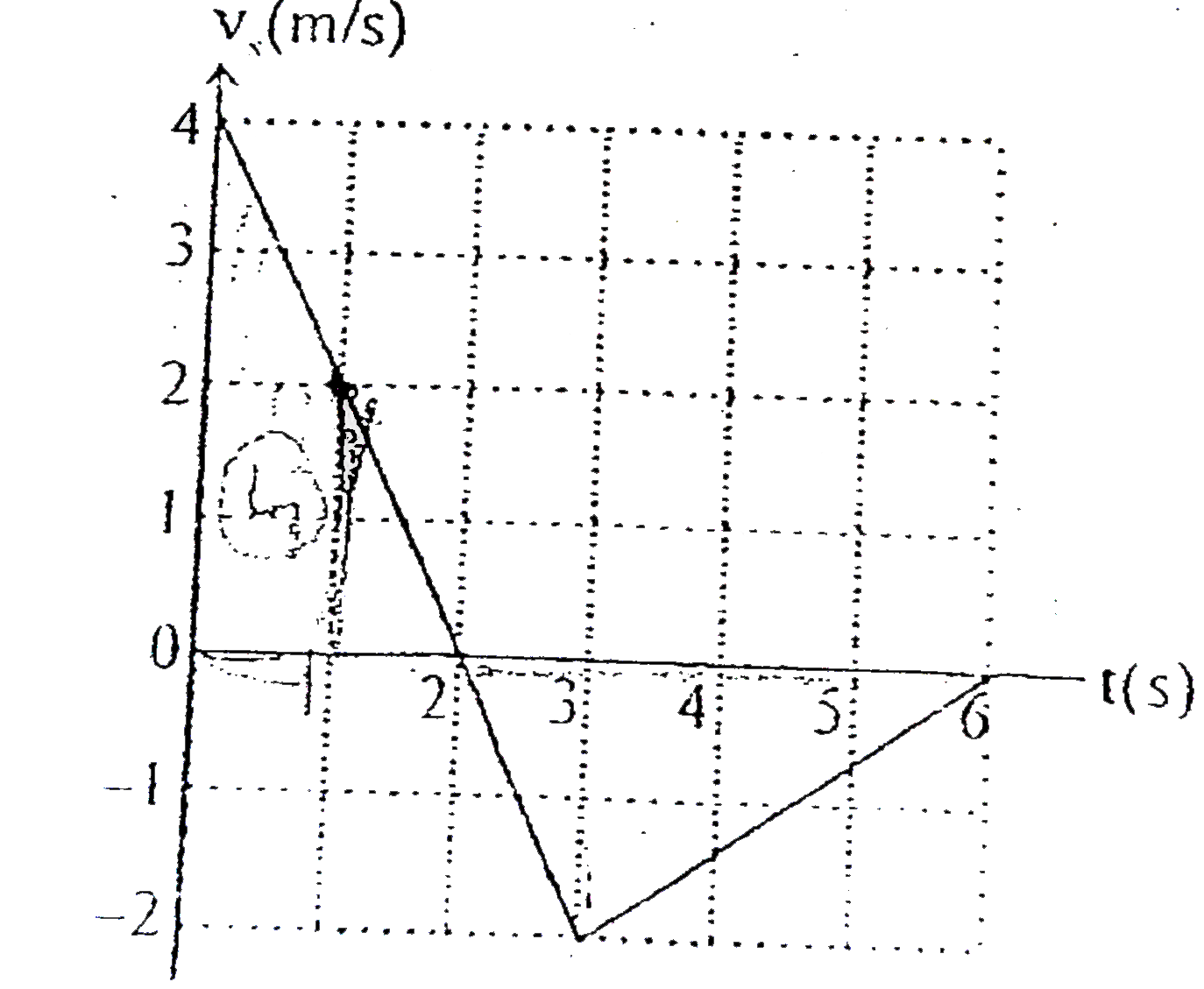
View Solution
