If the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
The correct Answer is:x=4
To find the position of the particle at t=2 seconds, given the velocity function v(t)=3t2−2t and the initial condition x(0)=0, we will follow these steps:
Step 1: Understand the relationship between velocity and position
Velocity is the rate of change of position with respect to time. Mathematically, this is expressed as:
v=dxdt
This implies that:
dx=vdt
Step 2: Substitute the velocity function into the equation
We substitute the given velocity function into the equation:
dx=(3t2−2t)dt
Step 3: Integrate both sides
To find the position x(t), we integrate the right side with respect to t:
x(t)=∫(3t2−2t)dt
Step 4: Perform the integration
We can integrate each term separately:
x(t)=∫3t2dt−∫2tdt
Calculating the integrals:
x(t)=3⋅t33−2⋅t22+C
This simplifies to:
x(t)=t3−t2+C
Step 5: Apply the initial condition
We know that when t=0, x(0)=0. We can use this to find the constant C:
x(0)=03−02+C=0⟹C=0
Thus, the position function simplifies to:
x(t)=t3−t2
Step 6: Calculate the position at t=2 seconds
Now, we can find the position at t=2:
x(2)=23−22=8−4=4
Final Answer
The position of the particle at t=2 seconds is:
4 meters
---
Velocity is the rate of change of position with respect to time. Mathematically, this is expressed as:
v=dxdt
This implies that:
dx=vdt
We substitute the given velocity function into the equation:
dx=(3t2−2t)dt
To find the position x(t), we integrate the right side with respect to t:
x(t)=∫(3t2−2t)dt
We can integrate each term separately:
x(t)=∫3t2dt−∫2tdt
Calculating the integrals:
x(t)=3⋅t33−2⋅t22+C
This simplifies to:
x(t)=t3−t2+C
We know that when t=0, x(0)=0. We can use this to find the constant C:
x(0)=03−02+C=0⟹C=0
Thus, the position function simplifies to:
x(t)=t3−t2
Now, we can find the position at t=2:
x(2)=23−22=8−4=4
The position of the particle at t=2 seconds is:
4 meters
Topper's Solved these Questions
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Graphs))
Explore 30 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Co-ordinate & Algebra)
Explore 39 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Differentiation)
Explore 40 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Example
Explore 1 Video
Similar Questions
If the velocity of a paraticle moving along x-axis is given as v=(4t2+3t=1)m/s then acceleration of the particle at t=1sec is :
View SolutionThe position of the particle moving along x-axis is given by x=2t−3t2+t3 where x is in mt and t is in second.The velocity of the particle at t=2sec is
View Solution
Knowledge Check
If the velocity of the a particle moving on x-axis is given by v=3t2−12t+6. at what time is the acceleration of particle zero ?
A2 secB2+√2secC2−√2secDzeroPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
AVelocity (i.edxdt) of particleBInitial velocity(i.edxdt att=0)CVelocity at t=2secDAccleration(i.ed2xdt2) of particlevx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
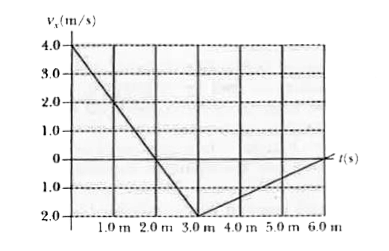 A−2.0 mB+2.0 mC+1.0 mD−1.0 m
A−2.0 mB+2.0 mC+1.0 mD−1.0 m
Position of particle moving along x-axis is given by x=2t^(3)-4t+3 Initial position of the particle is
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3s
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionA particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
View SolutionPosition of a particle moving along x-axis is given by x=2+8t−4t2. The distance travelled by the particle from t=0 to t=2 is:-
View Solution

