Velocity (in m/s) of a particle moving along x-axis varies with time as, $v = (10 + 5 t - t^{2})$ At time $t = 0, x = 0 .$ Find
(a) acceleration of particle at $t = 2 s$ and
(b) x-coordinate of particle at $t = 3 s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

(a) $a = \frac{d v}{d t} = 5 - 2 t$
At $t = 2 s$
$a = 1 m s^{2}$
(b) $x = \int_{0}^{3} v d t = \int_{0}^{3} (10 + 5 t - t^{2}) d t$
$= {[10 t + 2.5 t^{2} - \frac{t^{3}}{3}]}_{0}^{2}$
$= (10 \times 3) + (2.5) {(3)}^{2} - \frac{{(3)}^{3}}{3}$
$= 43.5 m$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is

A $3 m / s^{2}$
B $- 5 m / s^{2}$
C $- 4 m / s^{2}$
D $2.5 m / s^{2}$
Question 2 - Select One
$v_{x}$ is the velocity of a particle moving along the x-axis as shown in the figure. If $x = 2.0 m$ at $t = 1.0 s,$ what is the position of the particle at $t = 6.0 s$ ?

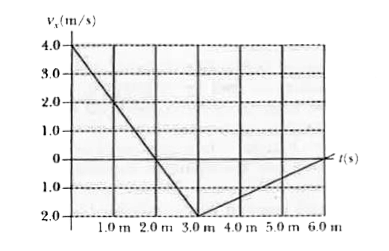A $- 2.0$ m
B $+ 2.0$ m
C $+ 1.0$ m
D $- 1.0$ m
Question 3 - Select One
the angular velocity omega of a particle varies with time t as $ω = 5 t^{2} + 25 r a \frac{d}{s}$ . the angular acceleration of the particle at $t = 1$ s is
A $10 r a \frac{d}{s^{2}}$
B $5 r a \frac{d}{s^{2}}$
CZero
D $3 r a \frac{d}{s^{2}}$

DC PANDEY-KINEMATICS-Exercise 6.6

Home
Ask Doubt
Profile