If u1 and u2 are the units selected in two systems of measurement and n1 and n2 their numerical values, then
n1u1=n2u2
n1u1+n2u2=0
n1n2=u1u2
(n1+u1)l=(n2+u2)
The correct Answer is:A
Pysical quantity (p)= numerical value (n)×unit(u) If pysical quantity remains constant then n∝1u ∵ n1u1=n2u2.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Fill in the blanks type
Explore 26 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Comprehension Type
Explore 31 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Multiple Correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
When some object is kept at a distances u1andu2 from the concave mirror then size of images are found to be same. If magnitude of focal length can be written as (u1+u2)/n, then what will be the value of n ?
|0123456789|
View SolutionTwo path 1 and 2 are shown in figure. If the change in internal energies are U1, and U2 for path 1 and 2 respectively, then
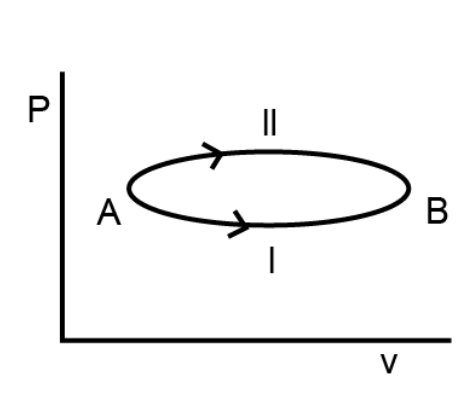
View Solution
Knowledge Check
If u1andu2 are the selected in two system of measurement and n1andn2 their nomerical values, then
An1u1=n2u2Bn1u1+n2u2=0Cn1n2=u1u2D(n1+u1)=(n2+u2)A physical quantity is measured and the result is expressed as nu where u is the unit used and n is the numberical value. If the result is expressed in various units then
An∝uBn∝u2Cn∝√uDn∝1uSTATEMENT 1 When the unit for measurement of a quantity is changed, its numerical value changes
STATEMENT 2 Smaller the unit of measurement matter is its numerical valueAStatement-1 is True , Statement-2 is True ,Statement-2 is a correct explanation for Statement-1BStatement-1 is True , Statement-2 is True ,Statement-2 is NOT a correct explanation for Statement-1CStatement-1 is True , Statement-2 is FalseDStatement-1 is False, Statement-2 is True
The numerical values and units of a physical quantity in two different system of units are n1,n2andu1,u2 respectively. Then
View SolutionLet ΔU1andΔU2 be the changes in energy of the system in the process A and B then.
View Solution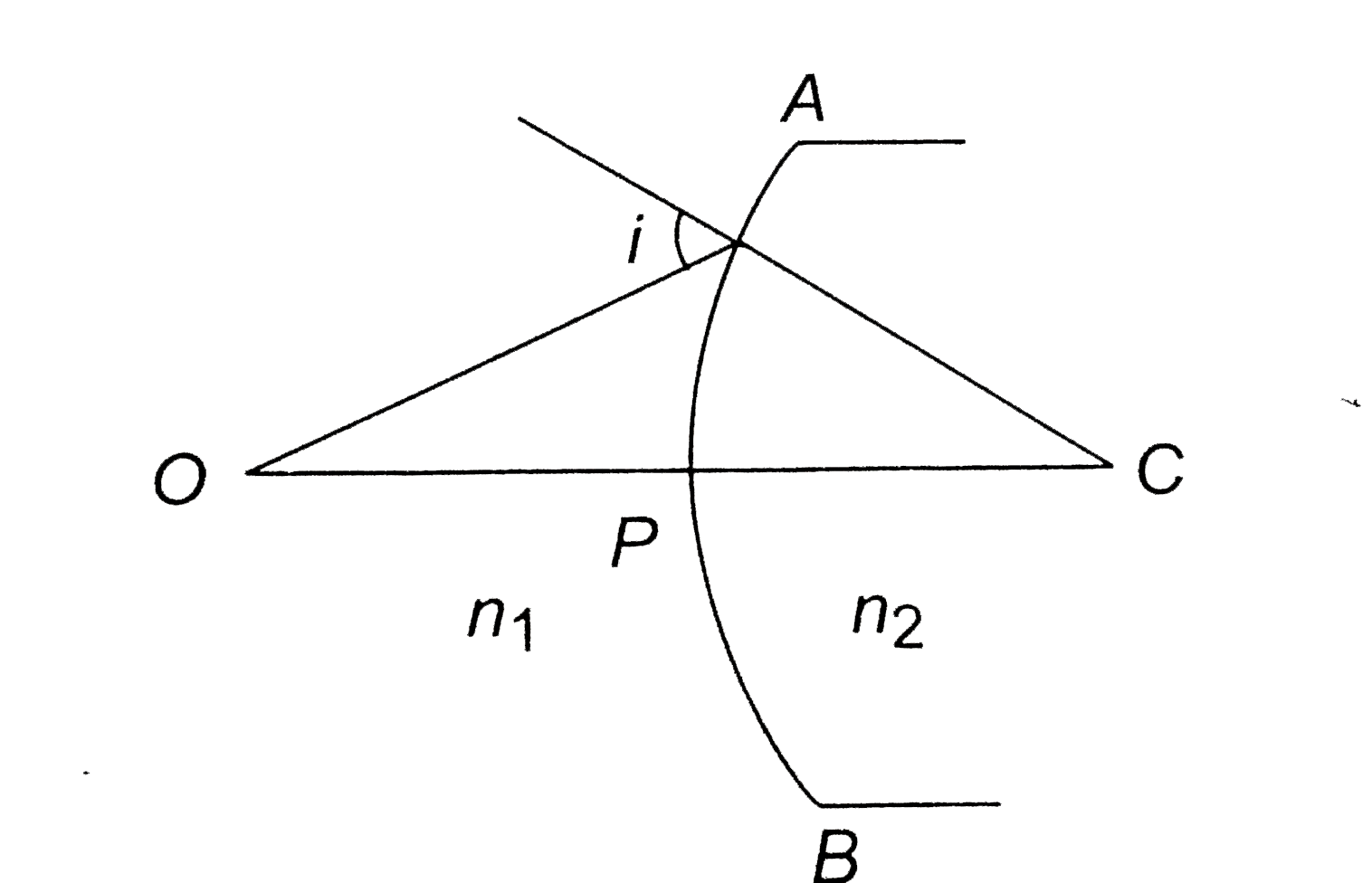
A point object O is kept at a distance OP=u The radius of curvature of the spherical surface APB is CP=R The refractive index of the media are n1 and n2 which are as shown in the diagram . Then,
(A) if n1>n2, image is virtual for all values of u
(B) if n2=2n1 image is virtual when R>u
(C) The image is real for all values of u, n1 and n2 here, the correct statements is/are
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
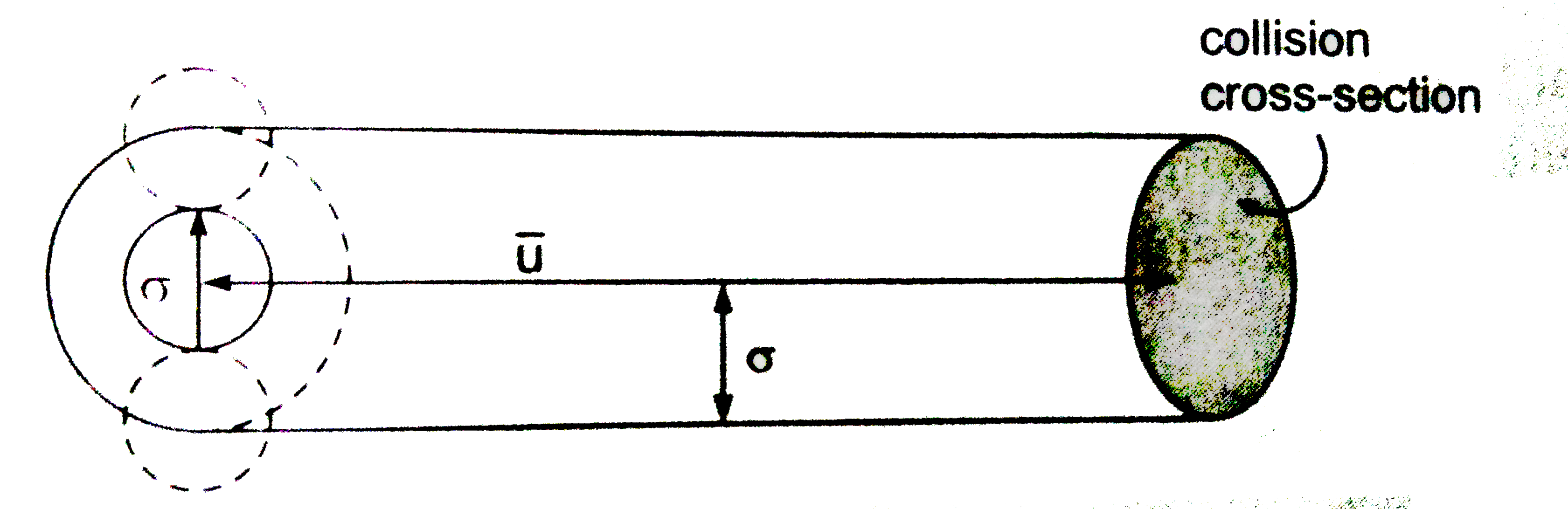
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
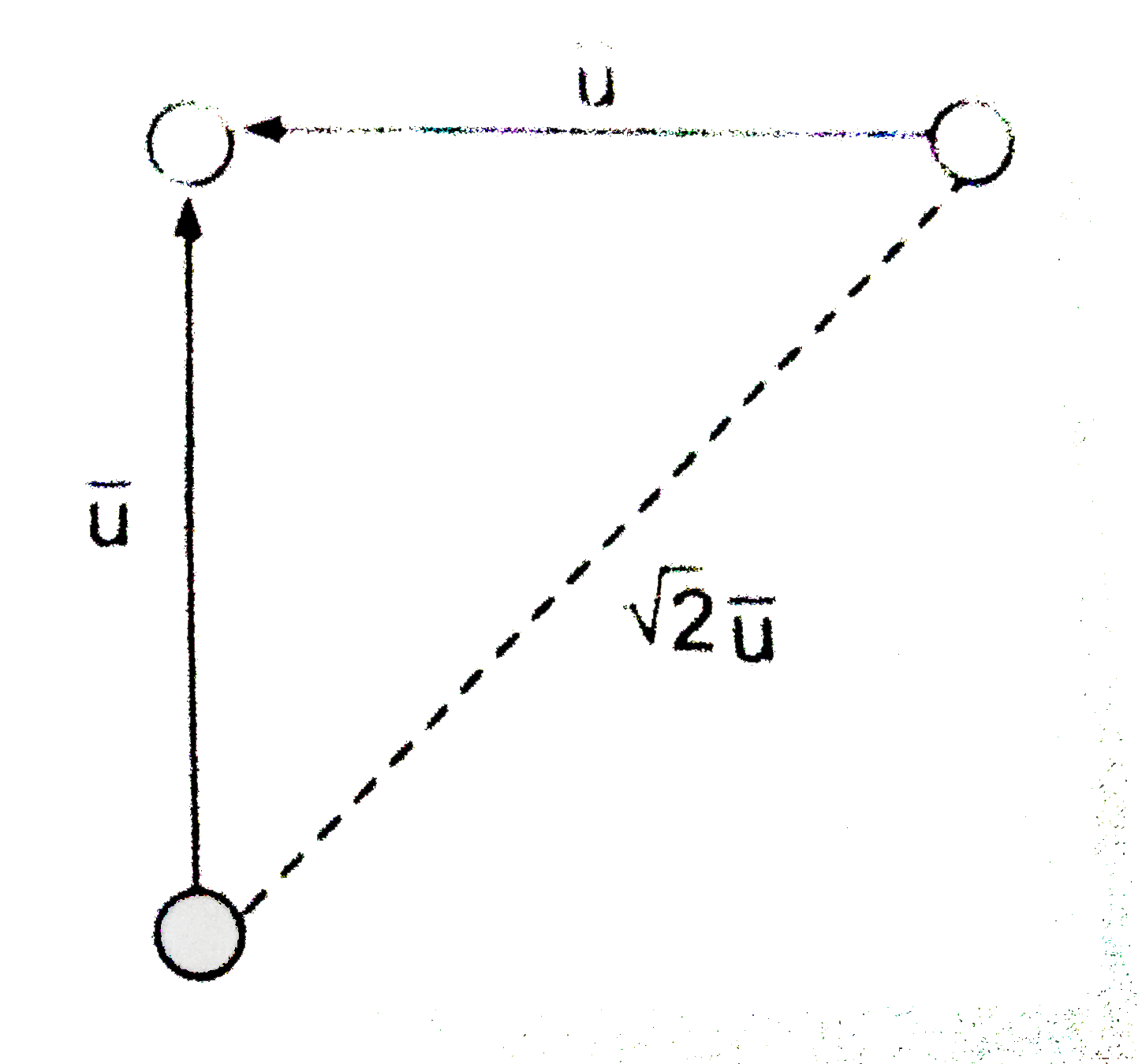
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate number of collision by one molecule per sec (Z1).
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
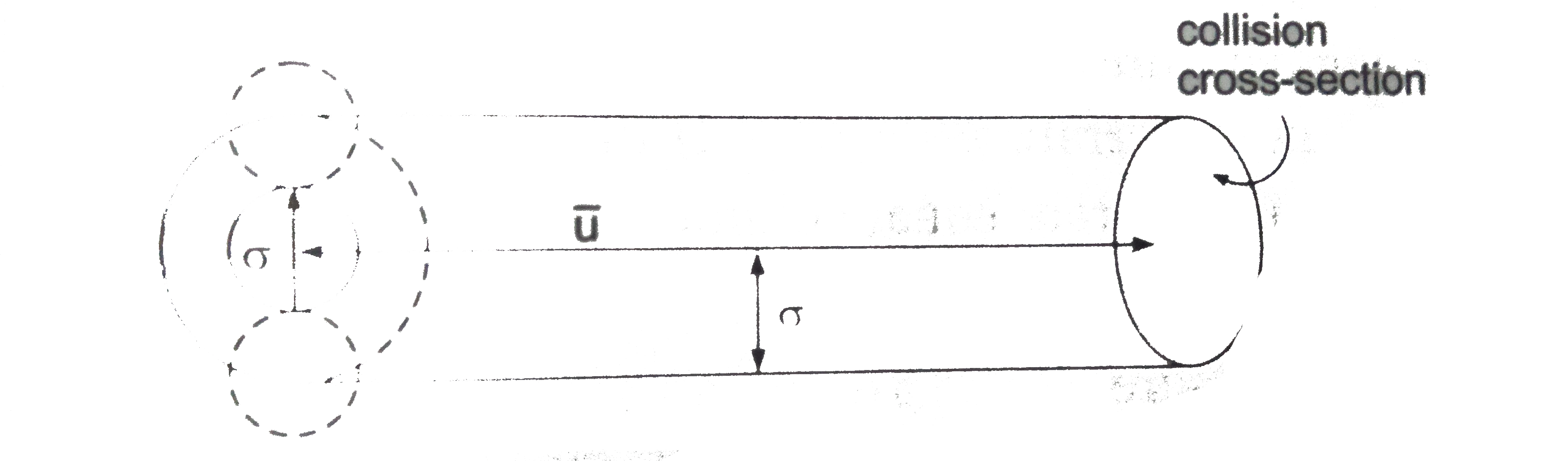
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
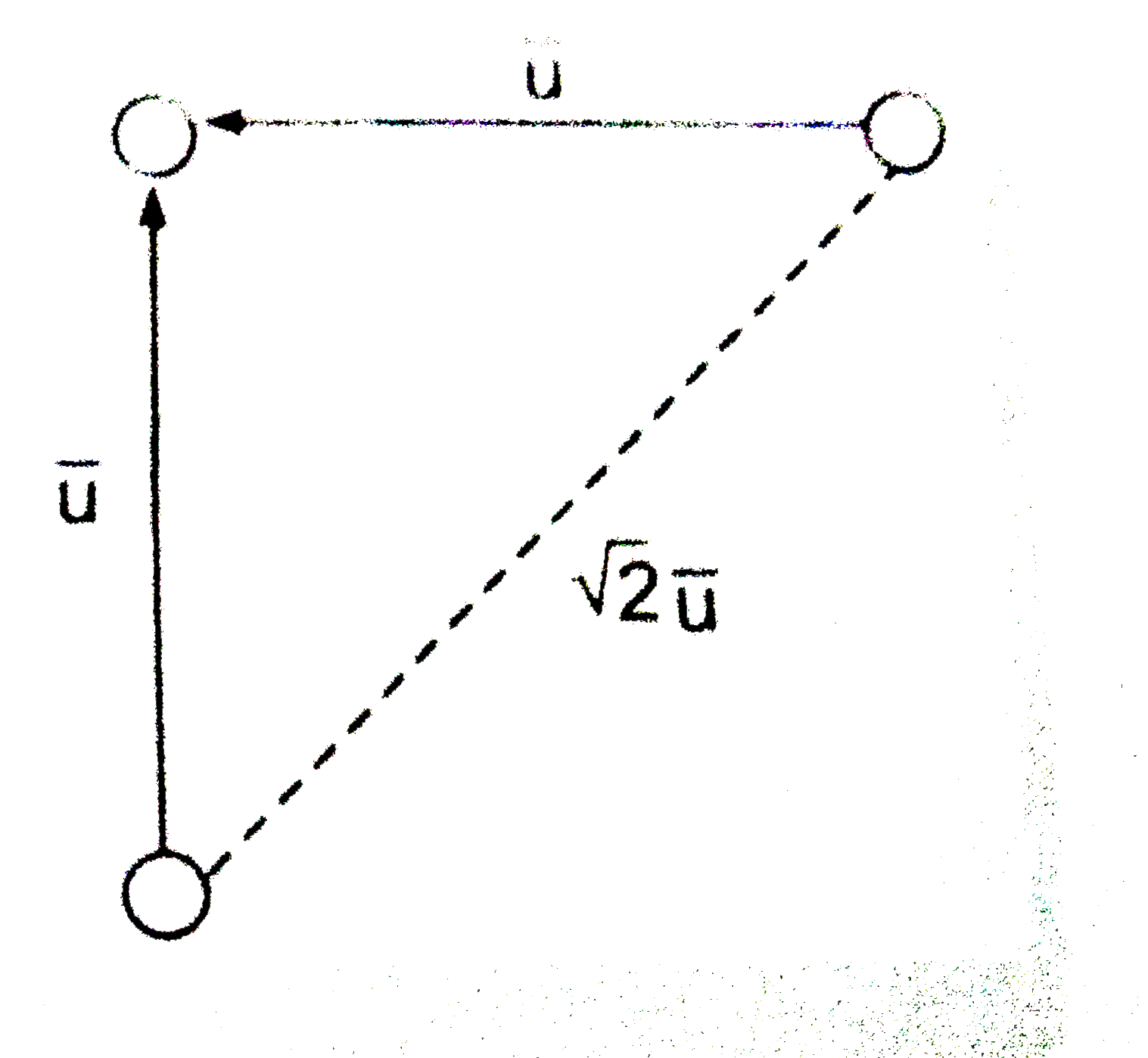
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View Solution

