A particle is projected from a horizontal floor with speed at an angle with the floor and striking the floor after sometime. State which is correct.
Velocity of particle will be perpendicular to initial direction two seconds after projection.
Minimum speed of particle will be .
Displacement of particle after half second will be m
The particle will strike the floor at 2 sec.
The correct Answer is:B, C
Min. speed
Displacement
sec
Thus, before 2 sec particle will strike the floor.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Single Correct Answer type
491 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - Fill in the blanks type
26 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICSCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICSCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONEXERCISE - Question Bank
38 Videos
Similar Questions
A ball is projected from a point on the floor wilth a speed of 15 m/s at an angle of 600 with the horizontal. Will ilt hit a vertical wall 5 m away from the point of projection and perpendiculaer to the plane of projection without and perpendicular to the plane of projection without hitting the floor? will the answer differ if the wall is 22 m away?
View SolutionA ball is projected from the floor of a cabin of height 7m with speed 20 m/s at an angle of 37∘ with the floor of cabin. It makes a successive collision with the wall of cabin and then return again to its floor. Assume all collisions are perfectly elastic. Find time taken (in sec) by the ball to reach the floor after collisions with the ceiling of cabin.
View Solution
Knowledge Check
A particle is projected with speed 10m/s at angle 60∘ with the horizontal. Then the time after which its speed becomes half of initial.
A12 secB1 secC√3/2secD√3/2secA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
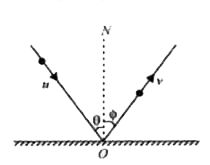 AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)A particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
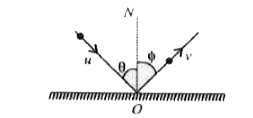 AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θ
AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θ
A particle A is projected with an initial velocity of 60 m/s. at an angle 30∘ to the horizontal. At the same time a second particle B is projected in opposite direction with initial speed of 50 m/s from a point at a distance of 100 m from A. If the particles collide in air, find (a) the angle of projection ∝ of particle B,
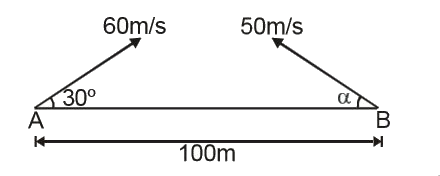
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
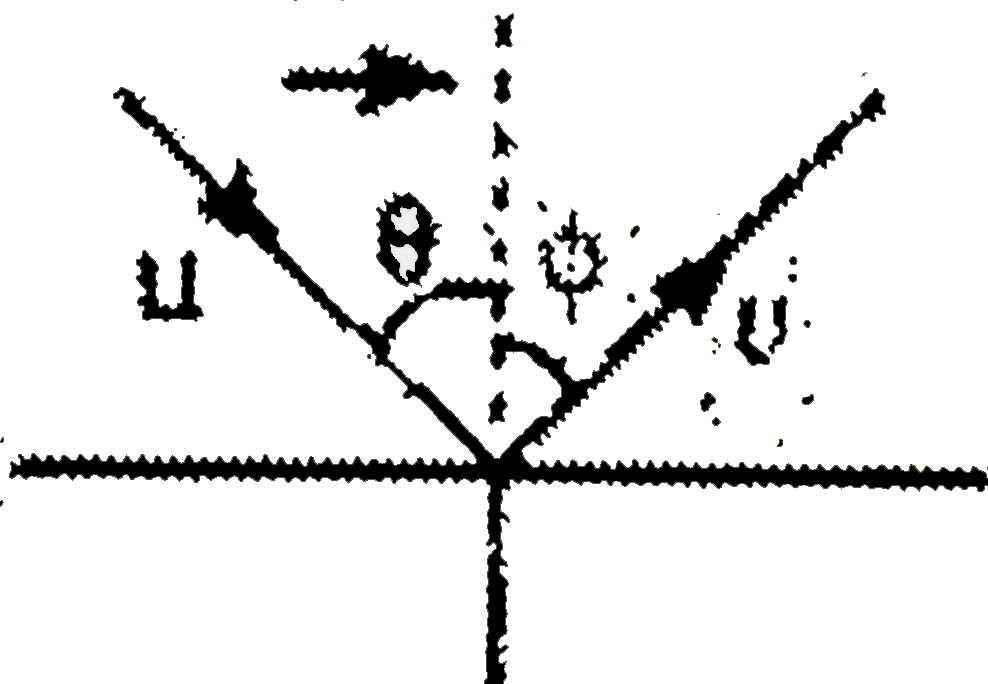
View Solution
